
86-2挠曲线的近似微分方程1.基本概念挠曲线方程:四转角w= w(x)V挠曲线挠度挠度w:截面形心W在y方向的位移xxw向上为正转角θ:截面绕中性轴转过的角度。θi逆钟向为正由于小变形,截面形心在x方向的位移忽略不计dv度转角关系为:0~ tan0:dx目录
6 §6-2 挠曲线的近似微分方程 1.基本概念 挠曲线方程: w = w(x) 由于小变形,截面形心在x方向的位移忽略不计 挠度转角关系为: dx dw tan = 挠曲线 y x x w 挠度 转角 挠度w:截面形心 在y方向的位移 w 向上为正 转角θ:截面绕中性轴转过的角度。 逆钟向为正 7-2 目录
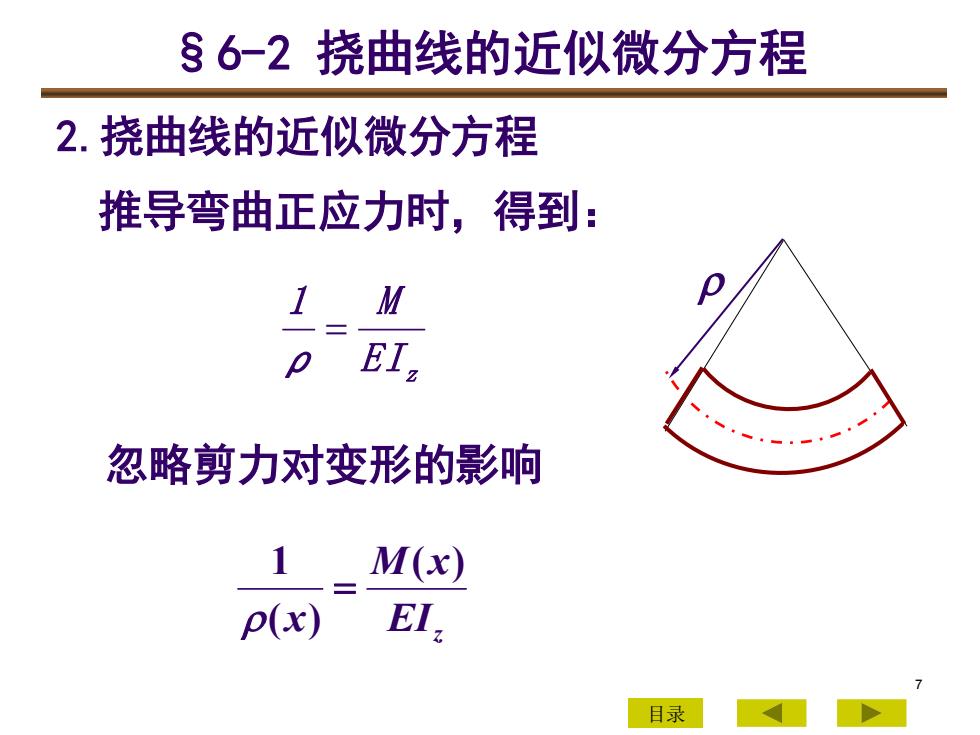
s6-2曲线的近似微分方程2.曲线的近似微分方程推导弯曲正应力时,得到:M7EI,0忽略剪力对变形的影响1M(x)EI,p(x)7目录
7 2.挠曲线的近似微分方程 推导弯曲正应力时,得到: E I z M ρ 1 = 忽略剪力对变形的影响 EIz M x x ( ) ( ) 1 = 目录 §6-2 挠曲线的近似微分方程

s6-2挠曲线的近似微分方程由数学知识可知:yd'yM(x) >0M(x)> 0dr?+O[1+()j3dy>0xdx0略去高阶小量,得yId22M(x)<0M(x) <0dr?pd'y<0dxxM(x)所以10?dr?EL,目录
8 由数学知识可知: 2 3 2 2 [1 ( ) ] 1 dx dy dx d y + = 略去高阶小量,得 2 2 1 dx d y = 所以 EIz M x dx d y ( ) 2 2 = 2 M(x) > 0 M(x) > 0 O d y dx 2 > 0 x y M(x) < 0 O dx d y 2 < 0 2 y x M(x) < 0 目录 §6-2 挠曲线的近似微分方程

86-2挠曲线的近似微分方程由弯矩的正负号规定可得,弯矩的符号与挠曲线的二阶导数符号一致,所以挠曲线的近似微分方程为:dwM(x)dx?EI由上式进行积分,就可以求出梁横截面的转角和挠度。目录
9 由弯矩的正负号规定可得,弯矩的符号与挠曲 线的二阶导数符号一致,所以挠曲线的近似微分方 程为: EI z M x dx d w ( ) 2 2 = 由上式进行积分,就可以求出梁横截面的转角 和挠度。 目录 §6-2 挠曲线的近似微分方程
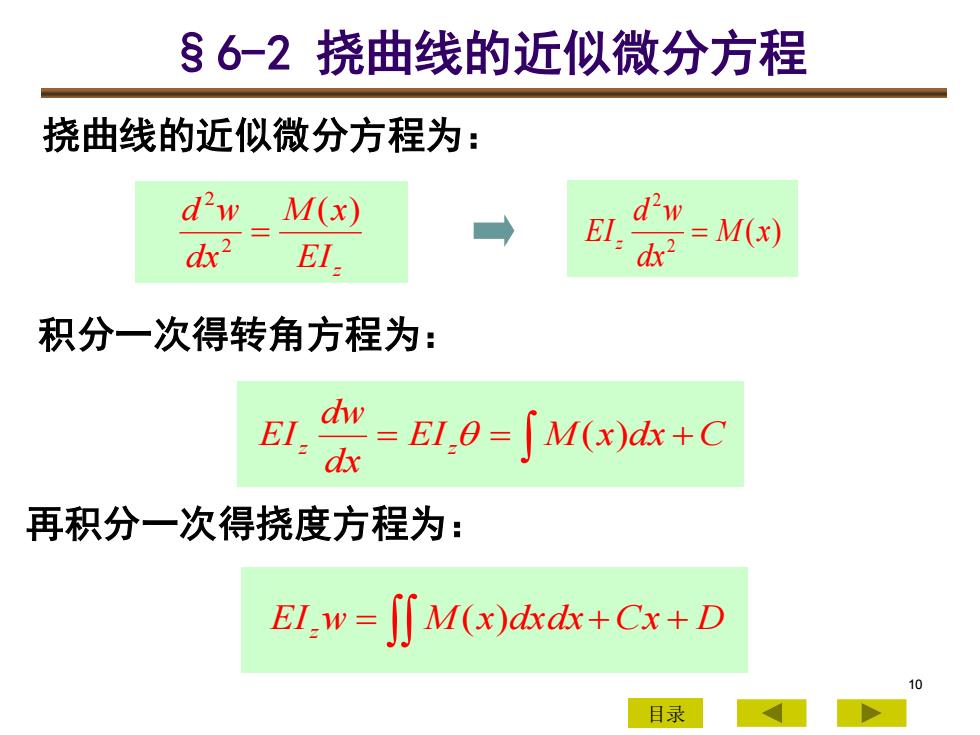
86-2挠曲线的近似微分方程挠曲线的近似微分方程为:M(x)1EIM(x)Edrdx积分一次得转角方程为:d= EI,0 =[ M(x)dx+CEIdx再积分一次得挠度方程为:EI,w= JJ M(x)dxdx+Cx + DC目录
10 挠曲线的近似微分方程为: EI z M x dx d w ( ) 2 2 = 积分一次得转角方程为: = EI = M x dx +C dx dw EIz z ( ) ( ) 2 2 M x dx d w EIz = 再积分一次得挠度方程为: EIz w = M (x)dxdx+Cx + D 7-3 目录 §6-2 挠曲线的近似微分方程