
Figure11:图与网络 斯解决哥尼斯堡七桥问题开始,欧拉建立了两门新的数学分支,即 “图论”(Graph Theory)或“组合”(Combinatorics)以及与庞加莱猜想密 切相关的“拓扑学”(Topology,欧拉当时称为“位置的几何学”(geometry of position),目前被广泛应用在各个领域. 11
Figure 11: ã❺✤ä ❞✮û①❩❞✄Ô①➥❑♠➞➜î✳ïá✡ü⑨★✛ê➷➞⑤➜❂ ✴ãØ✵(Graph Theory)➼✴⑤Ü✵(Combinatorics)➧✾❺✡❭✹ß➂➋ ❷❷✬✛✴ÿ➚➷✵(Topology➜î✳✟➒→➃✴➔➌✛❆Û➷✵(geometry of position))➜✽❝✚✷➁❆❫✸❼❻✰➁. 11

路 Figure12:世界第二公式 众所周知的著名公式、俗称“世界第二公式”即出自欧拉的“拓扑 学”: 欧拉示性数公式(Euler Characteristic Formula)一个凸多面体的 项点数v,边数e和面数f满足条件 v-e+f=2. 欧拉示性数公式最早由笛卡尔发现(v+∫=e+2),但欧拉发现了交错 和的形式,并将其重新写为 v-e+f=X. 12
Figure 12: ➢✳✶✓ú➟ ➥↕➧⑧✛❮➯ú➟✦❶→✴➢✳✶✓ú➟✵❂Ñ❣î✳✛✴ÿ➚ ➷✵➭ î✳➠✺êú➟(Euler Characteristic Formula) ➌❻àõ→◆✛ ➸✿ê v➜❃ê eÚ→ê f ÷✈❫❻ v − e + f = 2. î✳➠✺êú➟⑩❅❞✭❦✏✉②(v + f = e + 2)➜✂î✳✉②✡✂❺ Ú✛✴➟➜➾òÙ➢★✕➃ v − e + f = χ. 12

DATANG.NET Figure13:笛卡尔 笛卡尔(RenéDescartes,1596.3.31-1650.2.11,法国著名哲学家、数学 家,被誉为现代西方哲学之父,解析几何学之父)建立了解析几何学,将几 何和代数联系了起来. 传说中的笛卡尔与瑞典女王克里斯蒂娜的第十三封情书只有一行字: r=a(1-sina) 13
Figure 13: ✭❦✏ ✭❦✏(Ren´e Descartes, 1596.3.31õ1650.2.11➜④■❮➯ó➷❬✦ê➷ ❬➜✚➍➃②➇Ü➄ó➷❷■➜✮Û❆Û➷❷■.)ïá✡✮Û❆Û➷➜ò❆ ÛÚ➇ê é❳✡å✺. ❉❵➙✛✭❦✏❺❛❀å✜➂♣❞✵❆✛✶➏♥➭➐Ö➄❦➌✶✐➭ r = a(1 − sin α) 13
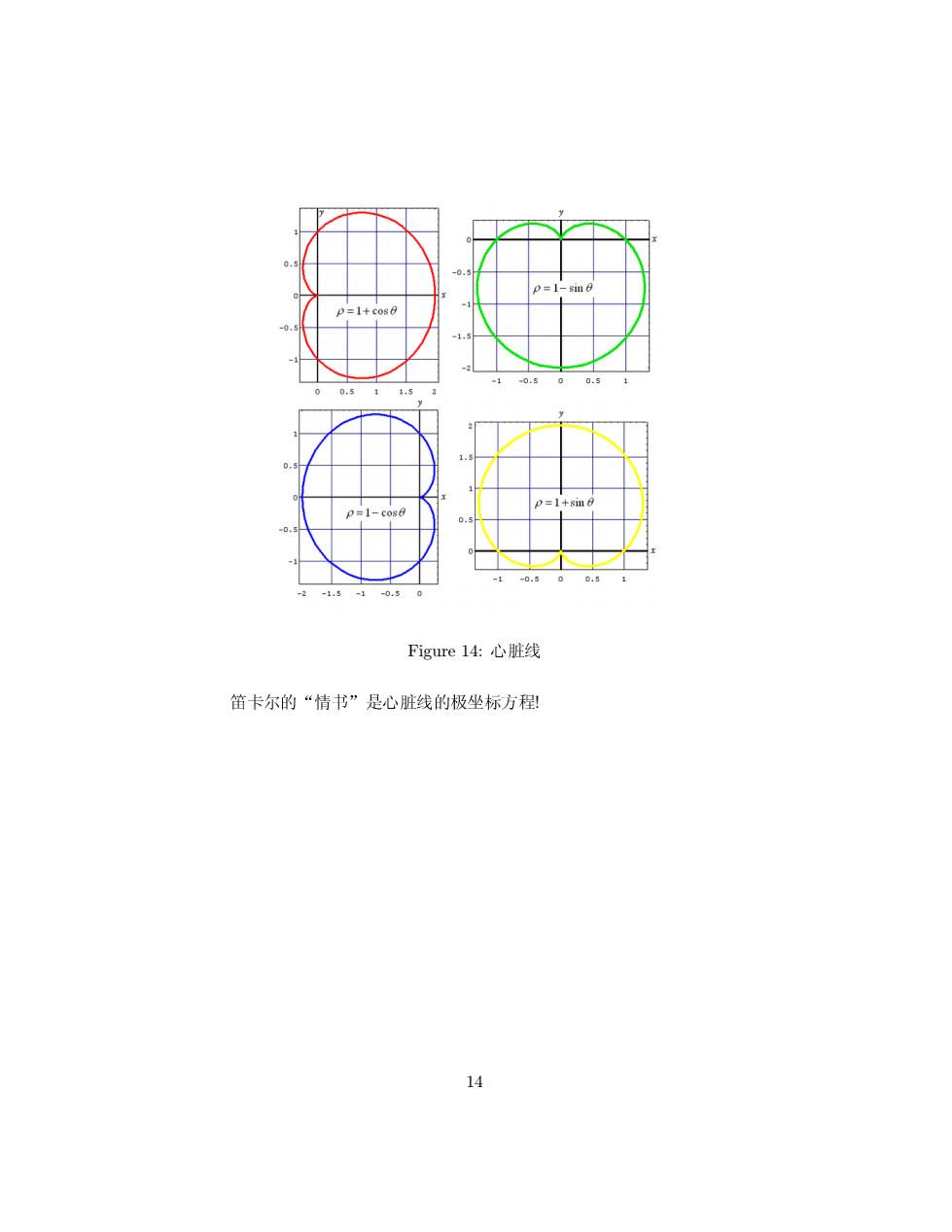
0. p=1-sin p=1+co80 =1 -0,5 0.5 0.5 1,5 1.5 0=+31110 p=1-cose 5 -1 -0.5 0.5 -2 1.5 -1 -0 Figure14:心脏线 笛卡尔的“情书”是心脏线的极坐标方程! 14
Figure 14: ✪✾❶ ✭❦✏✛✴➐Ö✵➫✪✾❶✛✹❿■➄➜! 14

Figure15:友谊定理之风车图 组合学中有众多趣味盎然的问题和定理,比如: 友谊定理(Friendship Theorem):在一群不少于三人的人中,若任 何两人都刚好只有一个共同认识的人,这群人中总有一人是所有人都认 识的。 (最简单的证明之一用到线性代数中的矩阵和特征值,完整的证明可以 在Proofs from the Book中找到.) 这个“所有人都认识的”人被称为“政治家”. 15
Figure 15: ❧➬➼♥❷➸➄ã ⑤Ü➷➙❦➥õ✕➏❭✱✛➥❑Ú➼♥➜✬❳➭ ❧➬➼♥(Friendship Theorem)➭✸➌✰Ø✟✉♥❁✛❁➙➜❡❄ Ûü❁Ñ❢Ð➄❦➌❻✁Ó❅↔✛❁➜ù✰❁➙♦❦➌❁➫↕❦❁Ñ❅ ↔✛✧ (⑩④ü✛②➨❷➌❫✔❶✺➇ê➙✛Ý✡Ú❆✍❾➜✑✒✛②➨➀➧ ✸Proofs from the Book➙é✔.) ù❻✴↕❦❁Ñ❅↔✛✵❁✚→➃✴✕↔❬✵. 15