
®OARD OF TRANSFORTA0 SEVEIl BRD©3s 0F+KO的HG5BERG Figure6:哥尼斯堡七桥 哥尼斯堡七桥问题是历史上有名的问题。这个问题是基于一个现实生 活中的事例:当时东普鲁士哥尼斯堡市区跨普列戈利亚河两岸,河中心有 两个小岛。小岛与河的两岸有七条桥连接。在所有桥都只能走一遍的前提 下,如何才能把这个地方所有的桥都走遍? 6
Figure 6: ①❩❞✄Ô① ①❩❞✄Ô①➥❑➫④↕þ❦➯✛➥❑✧ù❻➥❑➫➘✉➌❻②➣✮ ➵➙✛➥ ⑦➭✟➒➚✃➦➡①❩❞✄➼➠➟✃✎④⑤æàü❲➜à➙✪❦ ü❻✂✑✧ ✂✑❺à✛ü❲❦Ô❫①ë✚✧✸↕❦①Ñ➄❯r➌❍✛❝❏ ❡➜❳Ûâ❯rù❻✴➄↕❦✛①Ñr❍➸ 6
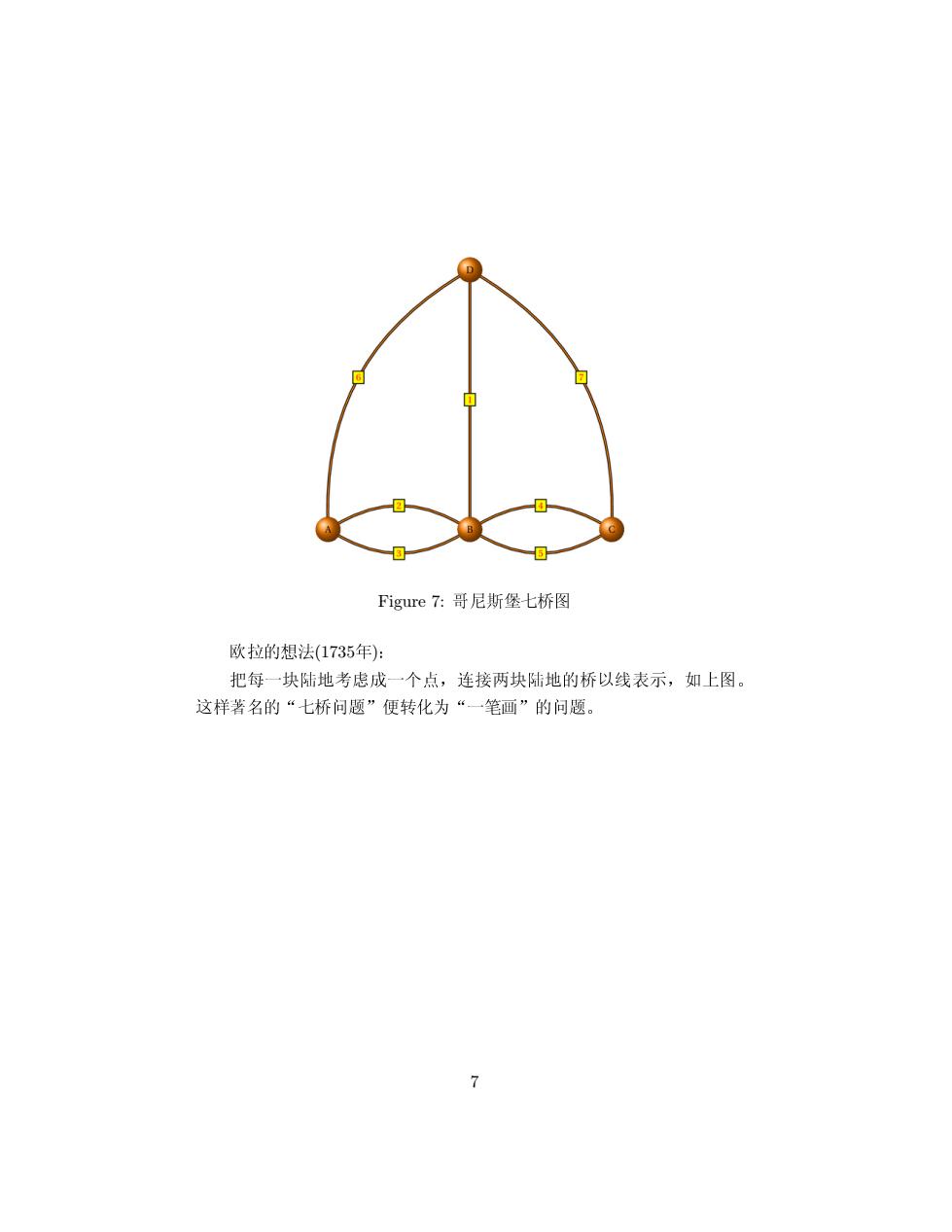
Figure7:哥尼斯堡七桥图 欧拉的想法(1735年): 把每一块陆地考虑成一个点,连接两块陆地的桥以线表示,如上图。 这样著名的“七桥问题”便转化为“一笔画”的问题。 7
Figure 7: ①❩❞✄Ô①ã î✳✛➂④(1735❝)➭ r③➌➡➸✴⑧➘↕➌❻✿➜ë✚ü➡➸✴✛①➧❶▲➠➜❳þã✧ ù✘❮➯✛✴Ô①➥❑✵❇❂③➃✴➌✮①✵✛➥❑✧ 7

Figure8:一笔哥 多边形显然可以一笔哥. 课题问答:五角星+五边形是否可以一笔哥?正方形加上两条对角线 是否可以一笔哥? 8
Figure 8: ➌✮① õ❃✴✇✱➀➧➌✮①. ➅❑➥❽➭✃✍✭+✃❃✴➫➘➀➧➌✮①➸✔➄✴❭þü❫é✍❶ ➫➘➀➧➌✮①➸ 8

unUU Figure9:一笔哥 欧拉的推理: 如果一个“图”能够一笔哥,那么对除去起点和终点外的每一个顶 点,必有一条离开它的边和一条进入它的边,因此以该点为一个顶点的边 的数目(称为该顶点的度)必为偶数(这样的顶点称为偶点)。因此,该图的 度数为奇数的顶点只能是起点或终点.如果起点等于终点,则该点也是偶 点,从而奇点的个数只能等于0或者2! 欧拉一笔哥定理一个连通图形可以一笔哥的充分必要条件是图的奇 点个数是0或2 推论:哥尼斯堡七桥问题无解。 课题问答与练习:正n(n≥4)边形加上其所有对角线是否可以一笔 哥? 9
Figure 9: ➌✮① î✳✛í♥➭ ❳❏➌❻✴ã✵❯✡➌✮①➜❅♦éØ✖å✿Ú➟✿✠✛③➌❻➸ ✿➜✼❦➌❫❧♠➜✛❃Ú➌❫❄❭➜✛❃➜ Ï❞➧❚✿➃➌❻➸✿✛❃ ✛ê✽(→➃❚➸✿✛Ý)✼➃óê(ù✘✛➸✿→➃ó✿)✧Ï❞➜❚ã✛ Ýê➃Ûê✛➸✿➄❯➫ å✿➼➟✿. ❳❏å✿✤✉➟✿➜❑❚✿➃➫ó ✿➜❧✌Û✿✛❻ê➄❯✤✉ 0 ➼ö 2! î✳➌✮①➼♥ ➌❻ëÏã✴➀➧➌✮①✛➾➞✼❻❫❻➫ã✛Û ✿❻ê➫0➼2. íØ➭①❩❞✄Ô①➥❑➹✮✧ ➅❑➥❽❺ö❙➭✔ n (n ≥ 4) ❃✴❭þÙ↕❦é✍❶➫➘➀➧➌✮ ①? 9

C 3 1 4 A 2 B 6 5 1 D Figure10:哥尼斯堡5桥 哥尼斯堡的七座桥二战时期被炸2座,另有2座被修成够高速公路。现 新修2座,共5座,其中“偶点”3个,“奇点”2个,因斯 哥尼斯堡5桥问题可解! 10
Figure 10: ①❩❞✄5① ①❩❞✄✛Ô➀①✓Ô➒Ï✚➾2➀➜✱❦2➀✚❄↕✡♣❸ú➫✧② ★❄2➀➜✁5➀➜Ù➙✴ó✿✵3❻➜✴Û✿✵2❻➜Ï❞ ①❩❞✄5①➥❑➀✮! 10