海南大学：《结构力学》课程教学资源（PPT课件）第十一章 矩阵位移法

结构力学一—第十一章矩阵位移法 洛南大学木建筑工程学院 (e) e) 元 (11-1) 单元坐标系中的单元杆端位移列阵为 (11-2) 17

17 结构力学—第十一章 矩阵位移法 土木建筑工程学院 单元坐标系中的单元杆端位移列阵为 ( ) ( ) 1 N 2 Q 3 4 N 5 Q 6 e e i i e e i i e j j j j f F f F f M f F f F f M                   = = =                               F F F （11-1） ( ) ( ) 1 2 3 4 5 6 e e i i e e i i e j j j j u v u v d d d q d d d q                   = = =                               δ δ δ （11-2）

结构力学—第十一章矩阵位移法 海南大学土木建筑工程学院 公式(11-3)和(11-4)给出了参照系为整体 坐标系时，分别使用广义方式和传统方式表示的单 元杆端力和杆端位移列阵。 整体坐标系中的单元杆端力列阵为 e) Fe M Fe (11-3) Fe M 18

18 结构力学—第十一章 矩阵位移法 土木建筑工程学院 公式（11-3）和（11-4）给出了参照系为整体 坐标系时，分别使用广义方式和传统方式表示的单 元杆端力和杆端位移列阵。 整体坐标系中的单元杆端力列阵为 ( ) ( ) 1 2 3 4 5 6 e e xi yi e e i i e j xj yj j f F f F f M f F f F f M                   = = =                               F F F （11-3）

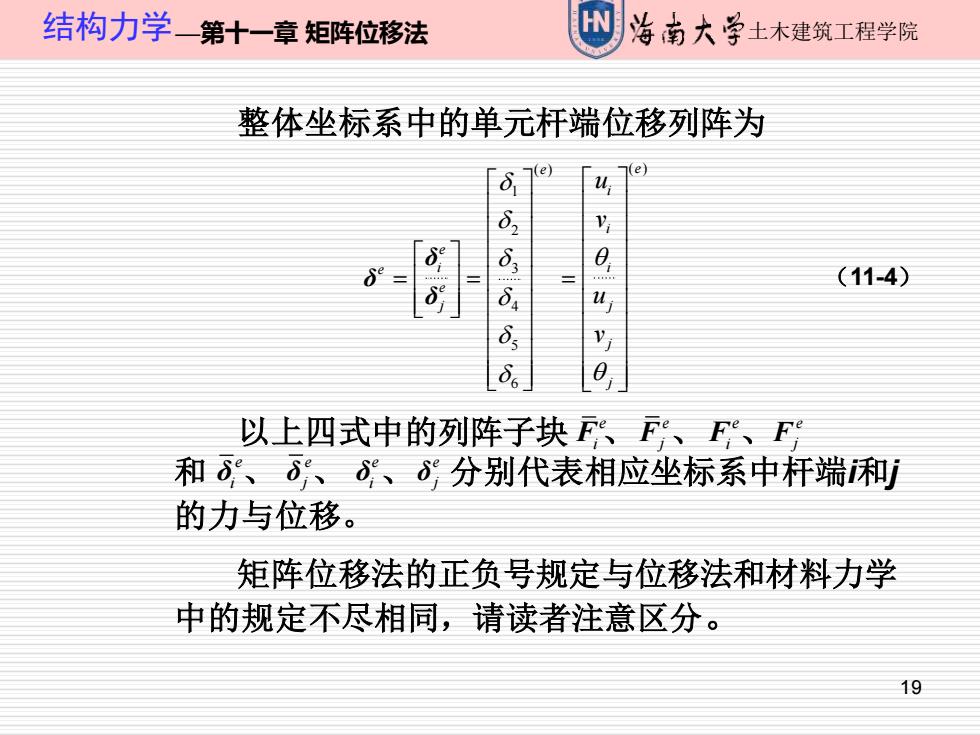
结构力学一第十一章矩阵位移法 W 治南大学土木建筑工程学院 整体坐标系中的单元杆端位移列阵为 (e) (11-4) 以上四式中的列阵子块、E、E、E 和δ、δ、6分别代表相应坐标系中杆端和j 的力与位移。 矩阵位移法的正负号规定与位移法和材料力学 中的规定不尽相同，请读者注意区分。 19

19 结构力学—第十一章 矩阵位移法 土木建筑工程学院 整体坐标系中的单元杆端位移列阵为 ( ) ( ) 1 2 3 4 5 6 e e i i e e i i e j j j j u v u v d d d q d d d q                   = = =                               δ δ δ （11-4） 以上四式中的列阵子块 、 、 、 和 、 、 、 分别代表相应坐标系中杆端i和j 的力与位移。 矩阵位移法的正负号规定与位移法和材料力学 中的规定不尽相同，请读者注意区分。 e Fi e Fj e Fi e Fj e δi e j δ e i δ e j δ

结构力学一第十一章矩阵位移法 海南大学土木建筑工程学院 1.3单元坐标系中的单元刚度矩阵 11.3.1一般单元 般单元是指其始末两端每端有三个、两端共 六个独立位移未知量的平面刚架单元，如下图所示。 E,I,A,1 20

20 结构力学—第十一章 矩阵位移法 土木建筑工程学院 11.3 单元坐标系中的单元刚度矩阵 11.3.1 一般单元 一般单元是指其始末两端每端有三个、两端共 六个独立位移未知量的平面刚架单元，如下图所示。 ui uj y FQj j F i v i Ni i FQi i1 E A Mi , I, j , l vj N j 1 Mj F j x

结构力学一—第十一章矩阵位移法 W 洛南大学士木建筑工程学院 表示单元杆端力和杆端位移之间转换关系的方 程，称为单元刚度方程。矩阵位移法不再忽略轴向 变形，但仍忽略在线弹性小变形的前提下，轴向受 力状态和弯曲受力状态间的相互影响。因此，可以 分别推导这两种受力状态下杆端力和杆端位移之间 的转换关系。 (1)轴向受力状态下，轴向杆端力同轴向杆 端位移之间的关系 如图（a),如果杆端发生轴向位移u而杆端 不动时，根据材料力学和平衡条件∑F=0,有 EA (a) 21

21 结构力学—第十一章 矩阵位移法 土木建筑工程学院 表示单元杆端力和杆端位移之间转换关系的方 程，称为单元刚度方程。矩阵位移法不再忽略轴向 变形，但仍忽略在线弹性小变形的前提下，轴向受 力状态和弯曲受力状态间的相互影响。因此，可以 分别推导这两种受力状态下杆端力和杆端位移之间 的转换关系 。 （1）轴向受力状态下，轴向杆端力同轴向杆 端位移之间的关系 如图（a），如果杆端i发生轴向位移 而杆端j 不动时，根据材料力学和平衡条件 F x = 0 ，有 Ni i EA F u l = Nj i EA F u l = − （a） i u