中国科学技术大学：《量子化学 Quantum Chemistry》课程教学资源（课件讲稿）Topic 3 多原子分子 multi-electrons system（4/4）金属配合物分子轨道理论

金属配合物晶体场理论 1.配合物的M0方法 3)、配体的σ-型群轨道 (SALC) 投影算子： galg ∑xag*(Ro R 用视察法，与原子轨道的函数图形对比。 Z ⊕ 01g g(aig) V6a+,+a+o+a+0,) >6

1. 配合物的MO方法 6 3)、配体的 -型 群轨道（SALC） 投影算子: 用视察法，与原子轨道的函数图形对比 。 1 ˆ 1 1 ) ˆ *( 1      R ga g a g R h a1g ： ( ) 61 1  1  2  3  4  5  6  g       Y X Z Y X Z s g(a1g) 金属配合物晶体场理论

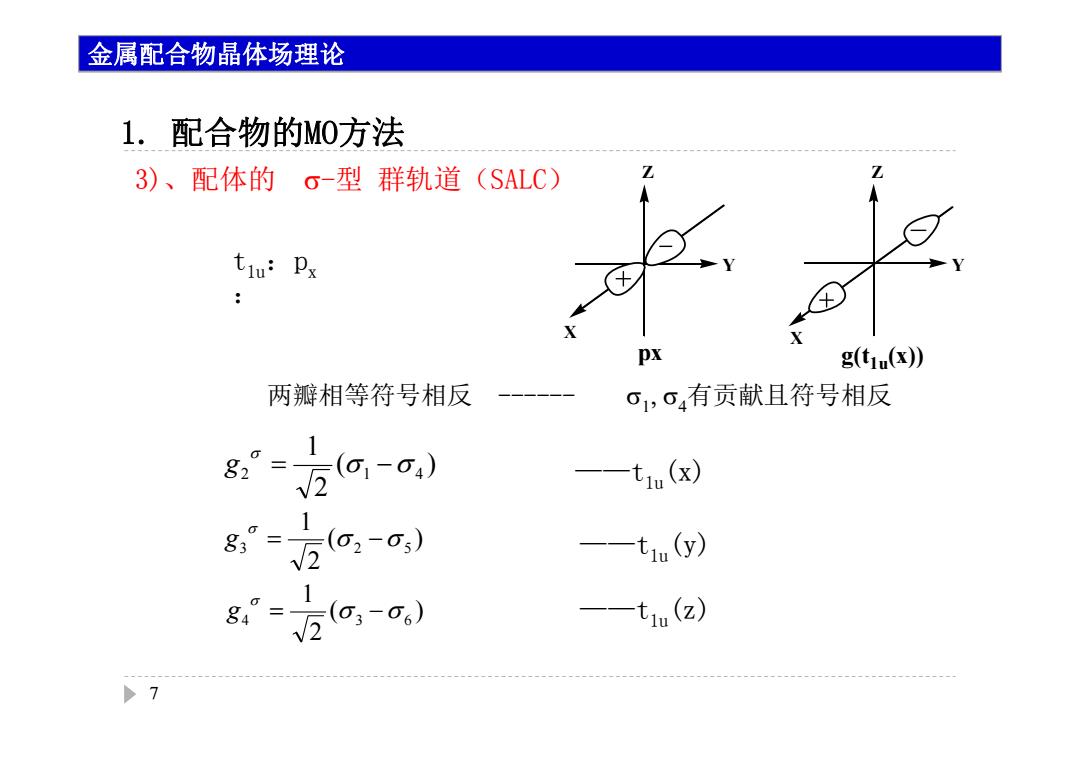
金属配合物晶体场理论 1.配合物的M0方法 3)、配体的6-型群轨道 (SALC) tiu:Px g(tu(x)) 两瓣相等符号相反--一-一一 01,04有贡献且符号相反 82°= tiu(x) 83= (G,-o,) --tu(（y) 84= --t1m(z)

1. 配合物的MO方法 7 t1u：px ： 两瓣相等符号相反 ------ 有贡献且符号相反 ——t1u(x) ( ) 21 2 1  4  g   ——t1u(y) ——t1u(z) ( ) 21 3  2  5  g   ( ) 21 4  3  6  g   Y X Z Y X Z px g(t1u(x)) 金属配合物晶体场理论 3)、配体的 -型 群轨道（SALC）

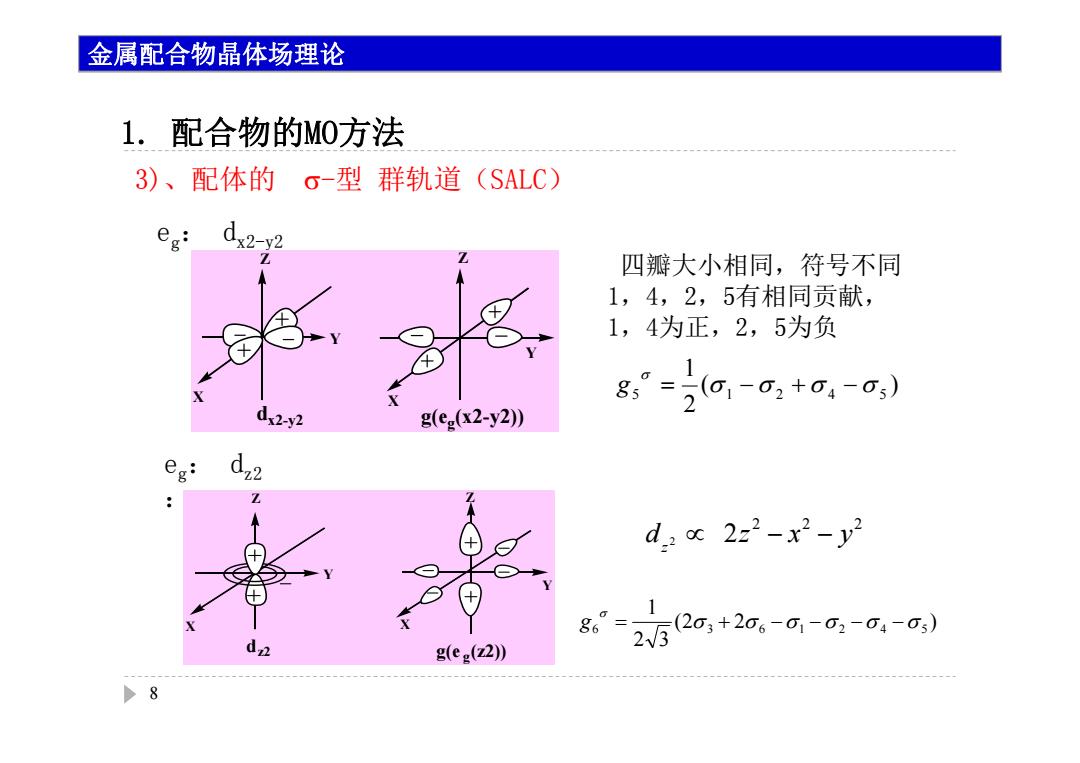
金属配合物晶体场理论 1.配合物的M0方法 3)、配体的6-型群轨道(SALC) 四瓣大小相同，符号不同 1,4,2,5有相同贡献， 1,4为正，2,5为负 5(01-02+04-05) x2-y2 g(ee(x2-y2)) eg: 2 d.:c 222-x2-y2 86= (203+206-01-02-04-03） 2W3 g(eg(z2)) >8

1. 配合物的MO方法 8 3)、配体的 -型 群轨道（SALC） eg： dx2-y2 eg： dz2 ： 四瓣大小相同，符号不同 1，4，2，5有相同贡献， 1，4为正，2，5为负 ( ) 21 5  1  2  4  5  g     (2 2 ) 2 31 6  3  6 1  2  4  5  g       Y X Z Y X Z dx2-y2 g(eg(x2-y2)) Y X Z Y X Z dz2 g(e g(z2)) 2 2 2 d 2 2z x y z    金属配合物晶体场理论

金属配合物晶体场理论 1.配合物的M0方法 4)、配合物的ō-型轨道作用 (配体的σ-型群轨道与金属中相应的轨道形成M0) a1galg=C+C281”成键 Walg*=C's+C2'g“反键 eg: "ge=C,d:+c4869 成键 "e*=c'd:+c4'8 反键 %gr2-吗=cd,-y+c%8, 成键 "egr-y*=c5'd,-y+c6'83 反键 (成键) (非键，金属轨道 >9

1. 配合物的MO方法 9 a1g： 成键   1 1 2 1 c s c g a g     1 1 2 1 a g *  c 's  c ' g 反键 —— 成键 —— 反键 —— 成键   ( 2 ) 3 2 4 g6 c d c eg z z eg：     ( ) 3 4 6 * ' ' 2 c d 2 c g eg z z     ( 2 2 ) 5 2 2 6 5 c d c g eg x y x y       ( ) 5 6 5 * ' ' 2 2 c d 2 2 c g eg x y x y     —— 反键 t1u：（成键） 4)、配合物的 -型 轨道作用 （配体的-型群轨道与金属中相应的轨道形成MO） t2g：（非键，金属轨道 ） 金属配合物晶体场理论