
随机变量及其分布 2)0≤F(x)≤1,limF(x)=0,limF(x)=1; X→-00 3)F心)是右连续函数,即对 x∈R,F(x+0)=F(x) 证3)由于Fx)单调不减,根据单调原理 仅需证,对任意的x∈R,有 -Fo 电子科技大学
随机变量及其分布 电子科技大学 2) 0 ( ) 1, lim ( ) 0, lim ( ) 1; F x F x F x x x 3) F(x)是右连续函数, 即对 x R, F(x 0) F(x). 证3)由于F(x)单调不减,根据单调原理 仅需证,对任意的x∈R, 有 ( ). 1 lim F x n F x n

随机变量及其分布 oo 因 ∩{X≤x+}={X≤x, n=] 2 且 X≤x+1}X≤x+23 D{X≤x+二}D… X x+1/2x+1 事件列X≤x+单调下降趋于≤,由概率 n 的连续性知性质3成立子科技大学
随机变量及其分布 电子科技大学 因 } { }, 1 { 1 X x n X x n } 1 { } 2 1 { 1} { n X x 且 X x X x ) …… ) ) x x+1/2 x+1 事件列 单调下降趋于{X≤x},由概率 的连续性知性质3成立. } 1 { n X x

随机变量及其分布 三、二维随机变量 定义1.2.3如果X和Y是定义在同一概率空 间(2,F,P)上的两个随机变量,称(X,Y)为二 维随机变量(向量). 思考 如何准确理解“维”的含义? 如何理解“定义在同一概率空间”? 电子科技大学
随机变量及其分布 电子科技大学 三、二维随机变量 定义1.2.3 如果X 和Y 是定义在同一概率空 间(Ω, F, P)上的两个随机变量, 称(X,Y )为二 维随机变量(向量). 如何准确理解“维”的含义? 如何理解“定义在同一概率空间” ? 思考:
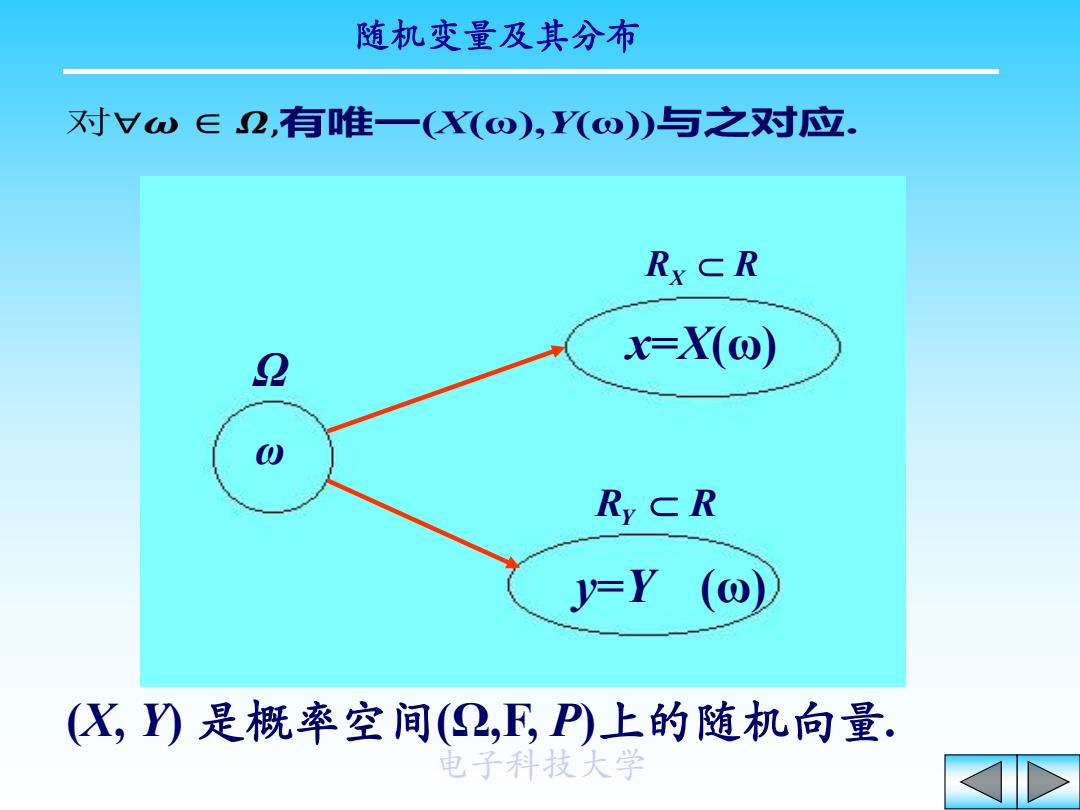
随机变量及其分布 对Vω∈2,有唯一(X(ω),Y(o)与之对应. RxCR 2 x-X(@) 0 Ry CR J=Y(@) (X,)是概率空间(2,F,P)上的随机向量. 电子科技大学
随机变量及其分布 电子科技大学 ω Ω x=X(ω) y=Y (ω) RX R RY R (X, Y) 是概率空间(Ω,F, P)上的随机向量

随机变量及其分布 Ex.1随机试验E:检查n个学生的健康情况,{心 表示抽检到第名学生,记样本空间为 2={1,2,…,n} 对于样本点∈2可定义 身高:X()会h, 体重:Y()会w. 身高X与体重Y构成定义在(2,可上的二维 随机变量(X,). EX2先抛一枚均匀硬币,再掷一颗均匀骰 子试验的样本空间为 电子科技大学
随机变量及其分布 电子科技大学 Ex.1 随机试验E: 检查n个学生的健康情况,{i} 表示抽检到第i 名学生,记样本空间为 Ω {1, 2,, n} 身高X与体重Y构成定义在(Ω, F)上的二维 随机变量(X, Y). EX.2 先抛一枚均匀硬币, 再掷一颗均匀骰 子试验的样本空间为