
第五章 定积分 不定积分 积分学 定积分
第五章 积分学 不定积分 定积分 定积分

第一为 第五章 定积分的桡念及性质 一、定积分问题举例 二、定积分的定义 三、定积分的性质 HIGH EDUCATION PRESS 自录 结
第一节 一、定积分问题举例 二、 定积分的定义 三、 定积分的性质 机动 目录 上页 下页 返回 结束 定积分的概念及性质 第五章
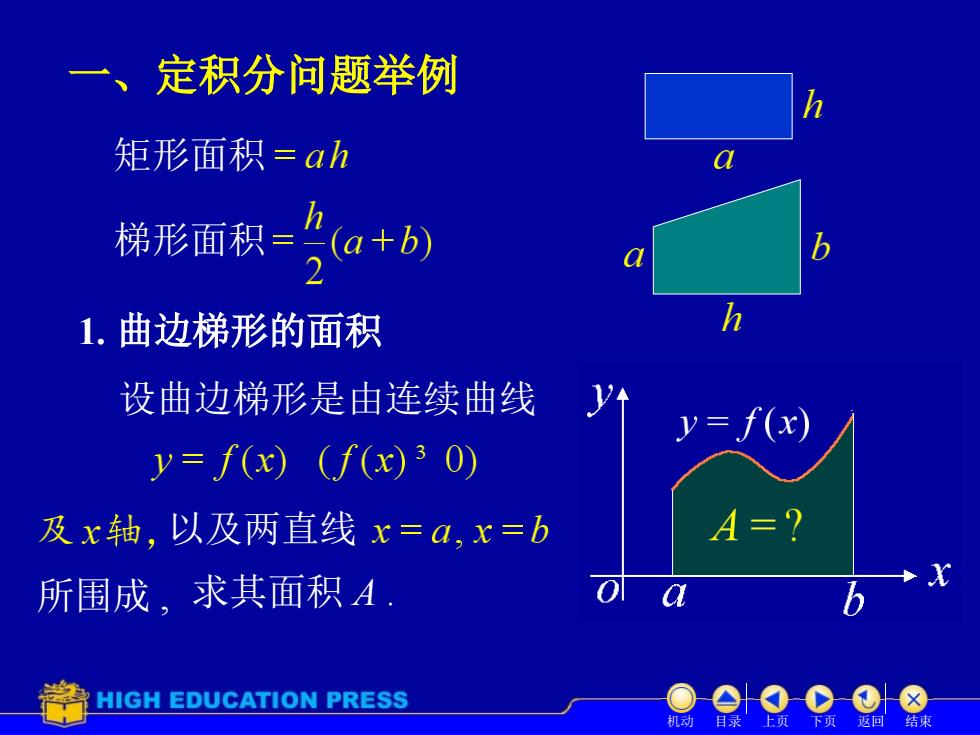
一、定积分问题举例 矩形面积=an h 梯形面积=(a+b) 1.曲边梯形的面积 设曲边梯形是由连续曲线 y=f(x)(f(x)30) 及x轴,以及两直线x=a,x=b 所围成,求其面积A: HIGH EDUCATION PRESS 结球
一、定积分问题举例 1. 曲边梯形的面积 设曲边梯形是由连续曲线 以及两直线 所围成 , 求其面积 A . 机动 目录 上页 下页 返回 结束 矩形面积 梯形面积
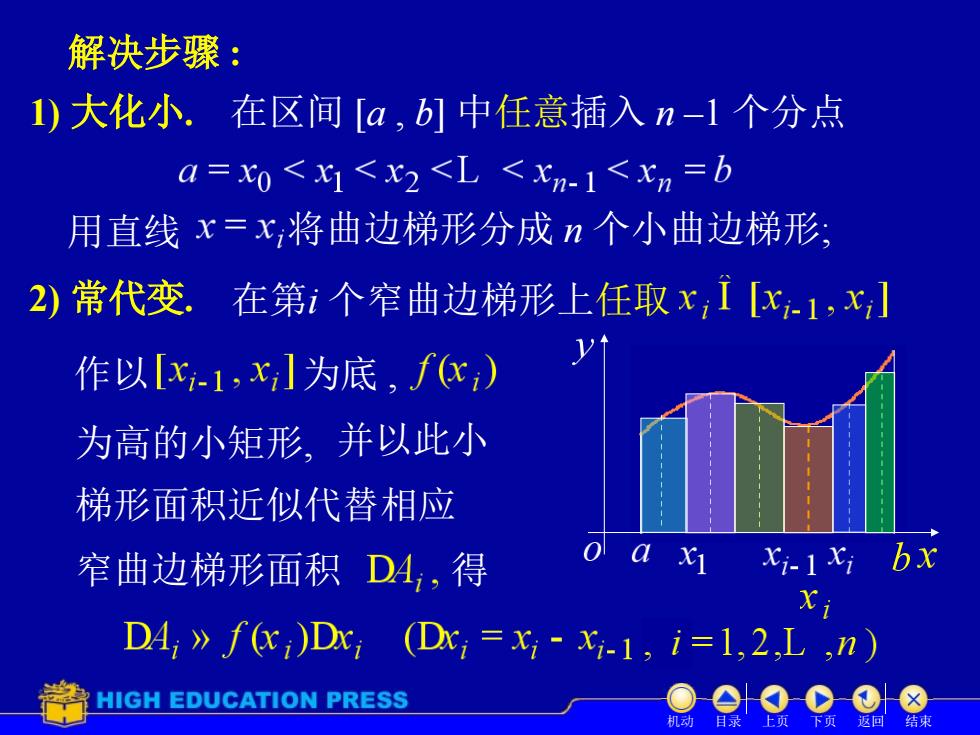
解决步骤: 1)大化小.在区间[a,b]中任意插入n-1个分点 a=x0<x1<x2<L <xn-1<xn=b 用直线x=x,将曲边梯形分成n个小曲边梯形 2)常代变,在第i个窄曲边梯形上任取x,1【x-1,x,] 1 作以[x-1,x]为底,fc,) 为高的小矩形,并以此小 梯形面积近似代替相应 窄曲边梯形面积DA,得 o a x xi-1xi bx D4,》fGc,)Dx,(Dx,=x-x-1,i=1,2,L,n) HIGH EDUCATION PRESS n 结球
解决步骤 : 1) 大化小. 在区间 [a , b] 中任意插入 n –1 个分点 用直线 将曲边梯形分成 n 个小曲边梯形; 2) 常代变. 在第i 个窄曲边梯形上任取 作以 为底 , 为高的小矩形, 并以此小 梯形面积近似代替相应 窄曲边梯形面积 得 机动 目录 上页 下页 返回 结束
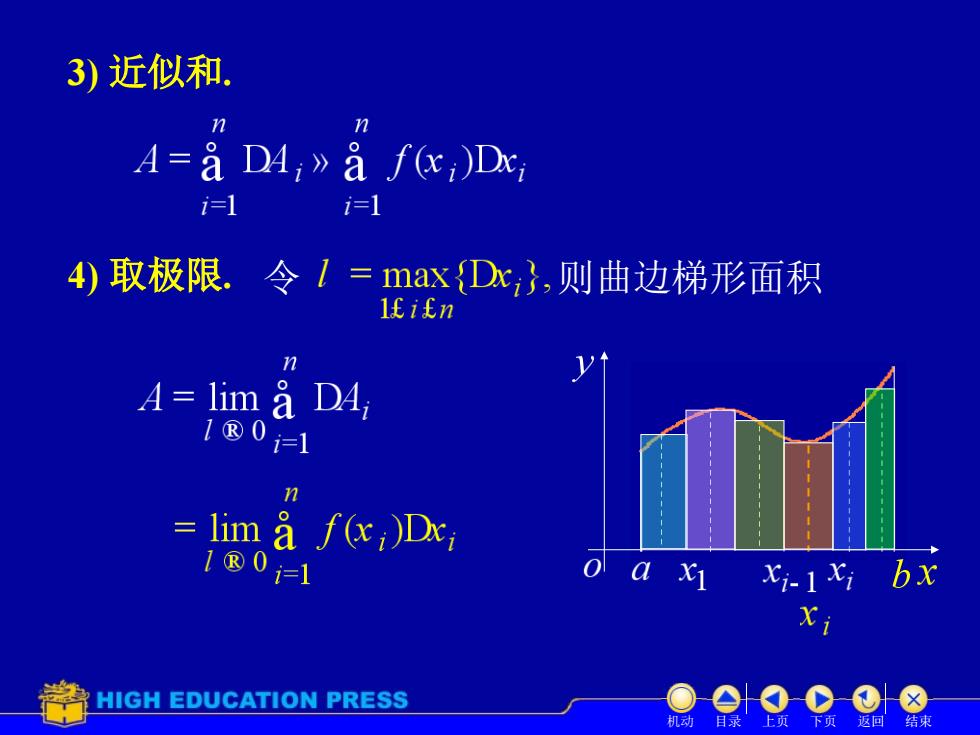
3)近似和. n n A=aDA,》afc,)Dx, i=1 i=1 4)取极限.令I=max {Dx,},则曲边梯形面积 IfiEn n A=lim a D4, 1®01 n lim a f(x)Dxi 1®01 o a x xi-1xi bx HIGH EDUCATION PRESS 结球
3) 近似和. 4) 取极限. 令 则曲边梯形面积 机动 目录 上页 下页 返回 结束