
Shanghai Jiao Tong University 1、劳斯判据的应用 ©判断系统的稳定性,以及根的大致分布情况 © 确定使系统稳定的参数取值范围 ©确定相对稳定性,即校验稳定裕量
Shanghai Jiao Tong University 1. 劳斯判据的应用 1. 劳斯判据的应用 判断系统的稳定性,以及根的大致分布情况 确定使系统稳定的参数取值范围 确定相对稳定性,即校验稳定裕量
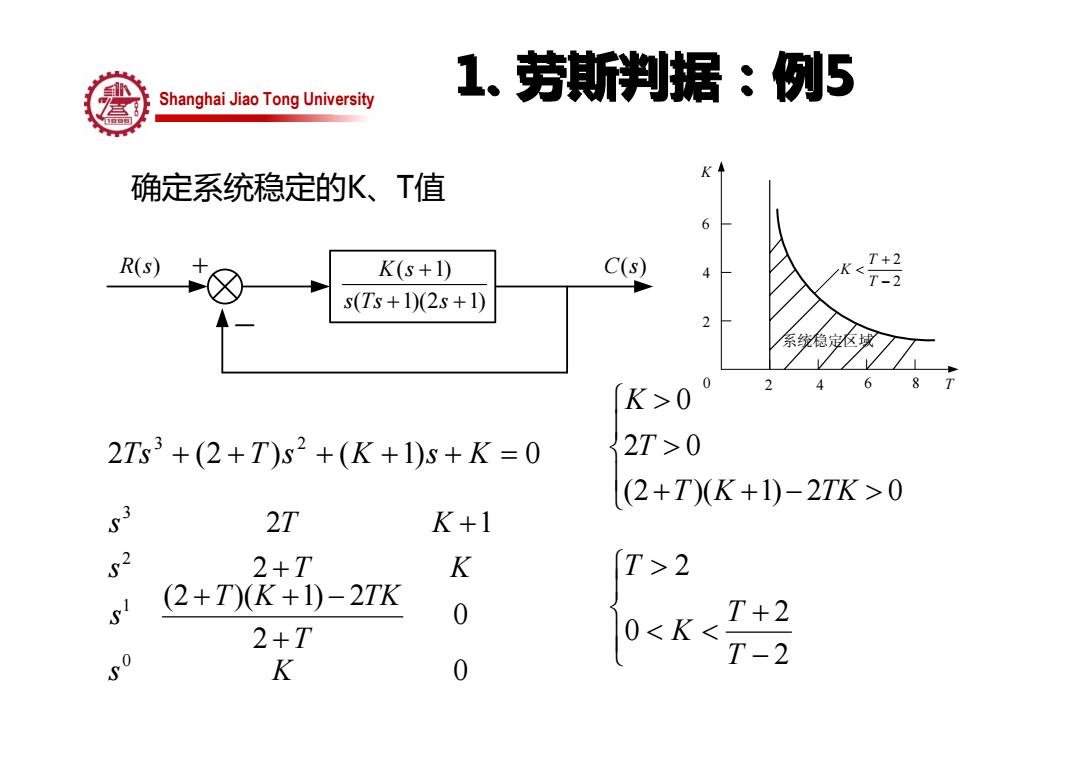
1.劳斯判据:例5 Shanghai Jiao Tong University 确定系统稳定的K、T值 6 R(s) K(s+1) C(s) 4 T-2 s(Ts+1)(2s+1) 2 系统稳定区域 K>0 2Ts3+(2+T)s2+(K+1)s+K=0 2T>0 (2+T)(K+1)-2TK>0 5 2T K+1 s 2+T K T>2 s (2+T)(K+1)-2TK 0 2+T 0<K< T+2 T-2 K 0
Shanghai Jiao Tong University 1. 劳斯判据:例5 1. 劳斯判据:例5 确定系统稳定的K、T值 ⎪⎩ ⎪⎨⎧ + + − > > > (2 )( 1) 2 0 2 0 0 T K TK T K ( 1) ( 1)(2 1) K s s Ts s + + + R s( ) + C s( ) − 2 (2 ) ( 1) 0 3 2 Ts + + T s + K + s + K = 0 0 2 (2 )( 1) 2 2 2 1 0 1 2 3 s K T T K TK s s T K s T K + + + − + + ⎪⎩ ⎪⎨⎧ − + < < > 2 2 0 2 T T K T K 0 T 2 2 4 4 6 6 8 2 2 T K T + < − 系统稳定区域

Shanghai Jiao Tong University 1.劳斯判据:例6 系统特征方程:53+8s2+10s+2=0 试判别系统的稳定性,并分析有几个根位于 [s] 垂线s=-1与虚轴之间。 Re s3 1 10 S=S1-1 s 1 -3 8 2 2 s3+5s2-3s1-1=0 5 -1 s 9.75 0 2.8 2 0 -1 全部根都 -6.5,-1,-0.5 有一个根 在S平台 在直线 左半平面 S=-1右侧
Shanghai Jiao Tong University 1. 劳斯判据:例6 1. 劳斯判据:例6 系统特征方程: 试判别系统的稳定性,并分析有几个根位于 垂线 s = -1 与虚轴之间。 2 0 9.75 0 8 2 1 10 0 1 2 3 s s s s s = s1 −1 5 3 1 1 0 21 3 s1 + s − s − = 1 0 2.8 0 5 1 1 3 0 1 1 1 2 1 3 1 − − − − s s s s Im −1 0 Re [s] ‐6.5,‐1,‐0.5 8 10 2 0 3 2 s + s + s + = 全部根都 在S平台 左半平面 有一个根 在直线 S=-1右侧

l、稳定性分析:Matlab ©模型创建 ·传递函数:sys=tf(num,den); 零极点/增益:Sys=zpk(Z,P,K); 状态空间:Sys=ss(A,B,C,D): 频率响应:frd 模型数据提取:tfdata,zpkdata,ssdata,frdata ©转换:tf,zpk,Ss,frd, ©运算:parallel,series,feedback © 零极点:pole,zero,pzmap
Shanghai Jiao Tong University1. 稳定性分析:Matlab 1. 稳定性分析:Matlab 模型创建 • 传递函数:sys = tf (num, den); • 零极点/增益: sys = zpk (Z, P, K); • 状态空间:sys = ss (A,B,C,D); • 频率响应:frd 模型数据提取:tfdata,zpkdata,ssdata, frdata 转换:tf,zpk,ss,frd,… 运算: parallel,series,feedback 零极点: pole,zero,pzmap

1.稳定性分析:Matlab实例 Shanghai Jiao Tong University 国 num=[1,2]; S+2 ©den=[1,2,3,1]; 国 gh tf(num,den); GH=g+2g2+3s+1 sys feedback(gh,1); s3+2s2+4s+3=0 国 [p,z]pzmap(sys) Pole-Zero Map p=-0.5+1.6583i 2 -0.5-1.6583i 1.5 -1.0 z=-2 0.5 [z,p,k]=zpkdata(sys); 国 p=pole(sys); ©z=zero(sys)i -0.5 ©roots([1243]) -1 -1.5 -1.5 7 0.5 Real Axis
Shanghai Jiao Tong University 1. 稳定性分析:Matlab实例 1. 稳定性分析:Matlab实例 num = [1,2]; den = [1,2,3,1]; gh = tf(num, den); sys = feedback(gh, 1); [p,z] = pzmap(sys) p = -0.5 + 1.6583i -0.5 - 1.6583i -1.0 z = -2 [z,p,k]=zpkdata(sys); p=pole(sys); z=zero(sys); roots([1 2 4 3]) 2 4 3 0 2 3 1 2 3 2 3 2 + + + = + + + + = s s s s s s s GH -2 -1.5 -1 -0.5 0 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 Pole-Zero Map Real Axis Imaginary Axis