
1.稳定性判别方法 Shanghai Jiao Tong University 直接求根 解微分方程:方程阶次较高时难以应用 。 根轨迹法(图解求根) ·绘制闭环极点随开环某参数变化的轨迹 ·利用计算机数值解或符号解 ©求特征根的范围 ·劳斯判据:根据特征方程系数判定(代数方法) Nyquist判据和Bode图(半图解法) ·根据开环频率特性判断闭环系统的稳定性 ·由于频率特性曲线易由实验获取,故该方法较实用 ©李雅普诺夫判据:用于非线性、任意阶系统 ©波波夫法:用于研究非线性鲁里叶型的时变系统 ©相平面法:多用于一、二阶非线性系统
Shanghai Jiao Tong University 1. 稳定性判别方法 1. 稳定性判别方法 直接求根 • 解微分方程:方程阶次较高时难以应用 • 根轨迹法(图解求根) • 绘制闭环极点随开环某参数变化的轨迹 • 利用计算机数值解或符号解 求特征根的范围 • 劳斯判据:根据特征方程系数判定(代数方法) • Nyquist判据和Bode图(半图解法) • 根据开环频率特性判断闭环系统的稳定性 • 由于频率特性曲线易由实验获取,故该方法较实用 李雅普诺夫判据:用于非线性、任意阶系统 波波夫法:用于研究非线性鲁里叶型的时变系统 相平面法:多用于一、二阶非线性系统

Shanghai Jiao Tong University 1.劳斯判据 系统稳定性 ·取决于特征根的分布 ·根是由闭环系统特征方程的系数决定的 ©劳斯(Routh)稳定判据 ·由特征方程的系数来分析系统的稳定性的一种代数判据 ©所有根均分布在左半平面的必要条件 ·设线性系统的特征方程为: ansn an-isn-1 +......as1 +ao=0 ·方程所有系数均为正数 ·若特征方程中任一系数为负或缺项(系数为零),则系统不稳定 ©适用条件 ·系统的特征方程为代数方程,且所有系数为实数
Shanghai Jiao Tong University 1. 劳斯判据 1. 劳斯判据 系统稳定性 • 取决于特征根的分布 • 根是由闭环系统特征方程的系数决定的 劳斯 (Routh) 稳定判据 • 由特征方程的系数来分析系统的稳定性的一种代数判据 所有根均分布在左半平面的必要条件 • 设线性系统的特征方程为: ansn + an-1sn-1 + …… + a1s1 + a0 = 0 • 方程所有系数均为正数 • 若特征方程中任一系数为负或缺项(系数为零),则系统不稳定 适用条件 • 系统的特征方程为代数方程,且所有系数为实数

Shanghai Tong Unversity1、劳斯判据:例 -0.77±0.9i 5s4+3s3+4s2+6=0 0.47±0.8i 5s4+4s3-2s2+3+5=0 -1±0.4i 0.6t0.68i 534+4s3+252+s+5=0 -0.87±0.7i 0.47±0.76i
Shanghai Jiao Tong University1. 劳斯判据:例 1. 劳斯判据:例 5 3 4 6 0 4 3 2 s + s + s + = 5 4 2 5 0 4 3 2 s + s − s + s + = 5 4 2 5 0 4 3 2 s + s + s + s + = ‐0.77 ± 0.9i 0.47 ± 0.8i ‐1 ± 0.4i 0.6 ± 0.68i ‐0.87 ± 0.7i 0.47 ± 0.76i

Shanghai J Tong University】、j 劳斯判据步骤 将特征方程式的系数 80 an-2 an-4 an-6… 按下列规则排成两行 an-3 an-5 an-7… b b, b3 ©建立劳斯表 Sh-3 C2 4…0444 ·又叫劳斯阵列 ©根据劳斯判据判别 b=da-idn-2-andn=3 b2=a-1-4-a,a-s 系统的稳定性 an- an- 表中第一列各值为正, b3=a1-14m-6-0,4n-7 则系统稳定; an-1 ·若劳斯表中第一列出 C1= ban-3-anb2 C,=bidr-s-drby 现负值,则系统不稳定 b b 实部为正的根的数目,等于表中第一列系数符号改变的次数
Shanghai Jiao Tong University1. 劳斯判据步骤 1. 劳斯判据步骤 将特征方程式的系数 按下列规则排成两行 建立劳斯表 • 又叫劳斯阵列 根据劳斯判据判别 系统的稳定性 • 表中第一列各值为正, 则系统稳定; • 若劳斯表中第一列出 现负值,则系统不稳定 • 实部为正的根的数目,等于表中第一列系数符号改变的次数 c c b b b ...... ...... s c c ...... s b b b ....... s a a a a ...... s a a a a ...... 1 1 5 1 3 2 1 1 3 1 2 1 1 1 6 7 3 1 1 4 5 2 1 1 2 3 1 1 2 n-3 1 2 3 n-2 n-1 n-3 n-5 n-7 n-1 n n-2 n-4 n-6 n b b a a b b b a a b a a a a a a a a a a a a a a a n n n n n n n n n n n n n n n n n n n − − − − − − − − − − − − − − − − − = − = − = − = − =
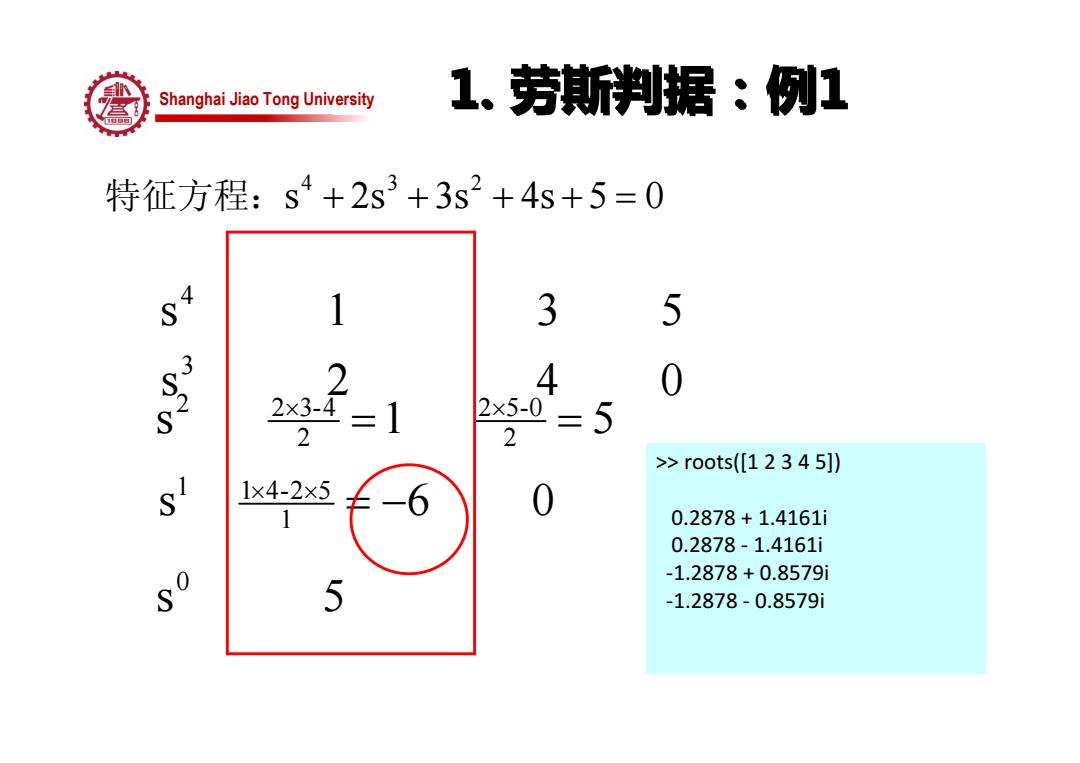
Shanghai Jiao Tong University 1.劳斯判据:例1 特征方程:S4+2s3+3s2+4s+5=0 1 3 5 23-=1 2 4 0 2×5-0 二 2 5 2 >>roots([12345]) s 1x4-2x5 1 0.2878+1.4161i 0.2878-1.4161i -1.2878+0.8579i 5 -1.2878-0.8579i
Shanghai Jiao Tong University 1. 劳斯判据:例1 1. 劳斯判据:例1 s 2s 3s 4s 5 0 4 3 2 + + + + = s 1 5 2 2 5-0 2 2 2 3-4 = = × × s 6 0 1 1 1 4-2 5 = − × × s 5 0 s 2 4 0 s 1 3 5 3 4 >> roots([1 2 3 4 5]) 0.2878 + 1.4161i 0.2878 ‐ 1.4161i ‐1.2878 + 0.8579i ‐1.2878 ‐ 0.8579i 特征方程: