
在周期场中,描述电子运动的Schrodinger方程为 [pUmpm 其中,U(r)=U(r+R)为周期性势场, R1141+122+l343为晶格格矢, 方程的解应具有下列形式: Ψk(r)=eikrug(r) Bloch函数 (Bloch wave function) 这里,4(r)=u(r+R)是以格矢R为周期的周期函数。 这个结果称为Bloch定理。它确定了周期势场中波动方程解的 基本特征
在周期场中,描述电子运动的Schrödinger方程为 ( ) ( ) ( ) 2 2 2 U r r E r m y y é ù - Ñ + = ê ú ë û h 其中,U(r) = U(r +Rl )为周期性势场, Rl =l1a1+l2a2+l3a3为晶格格矢, 方程的解应具有下列形式: ( ) ( ) i y e u × k k = k r r r —— Bloch函数 这里,uk (r) = uk (r +Rl ) 是以格矢 Rl 为周期的周期函数。 这个结果称为Bloch定理。它确定了周期势场中波动方程解的 基本特征。 (Bloch wave function)

换句话说:Boch发现,不管周期势场的具体函数形式如何, 在周期势场中运动的单电子的波函数不再是平面波,而是 调幅平面波,其振幅也不再是常数,而是按晶体的周期而 周期变化。如下页图表示。 这种形式的波函数 y(r)=ekru(r) 叫Bloch波函数,或说Bloch波。它描述的电子叫Bloch电子 这个结论称Bloch定理。B引och定理也可表述为: (f+)=ey.( 它表明在不同原胞的对应点上,波函数只相差一个相位因子 e),它不影响波函数的大小,所以电子出现在不同原胞的 对应点上几率是相同的。这是晶体周期性的反映
换句话说:Bloch 发现,不管周期势场的具体函数形式如何, 在周期势场中运动的单电子的波函数不再是平面波,而是 调幅平面波,其振幅也不再是常数,而是按晶体的周期而 周期变化。如下页图表示。 ( ) ( ) i y e u × k k = k r 这种形式的波函数 r r 叫 Bloch波函数,或说 Bloch 波。它描述的电子叫 Bloch电子 这个结论称 Bloch 定理。Bloch 定理也可表述为: ( ) ( ) ( ) i k Rn n k k y y r R e r × + = r ur r ur r 它表明在不同原胞的对应点上,波函数只相差一个相位因子 ,它不影响波函数的大小,所以电子出现在不同原胞的 对应点上几率是相同的。这是晶体周期性的反映。 i(k Rn ) e × r ur
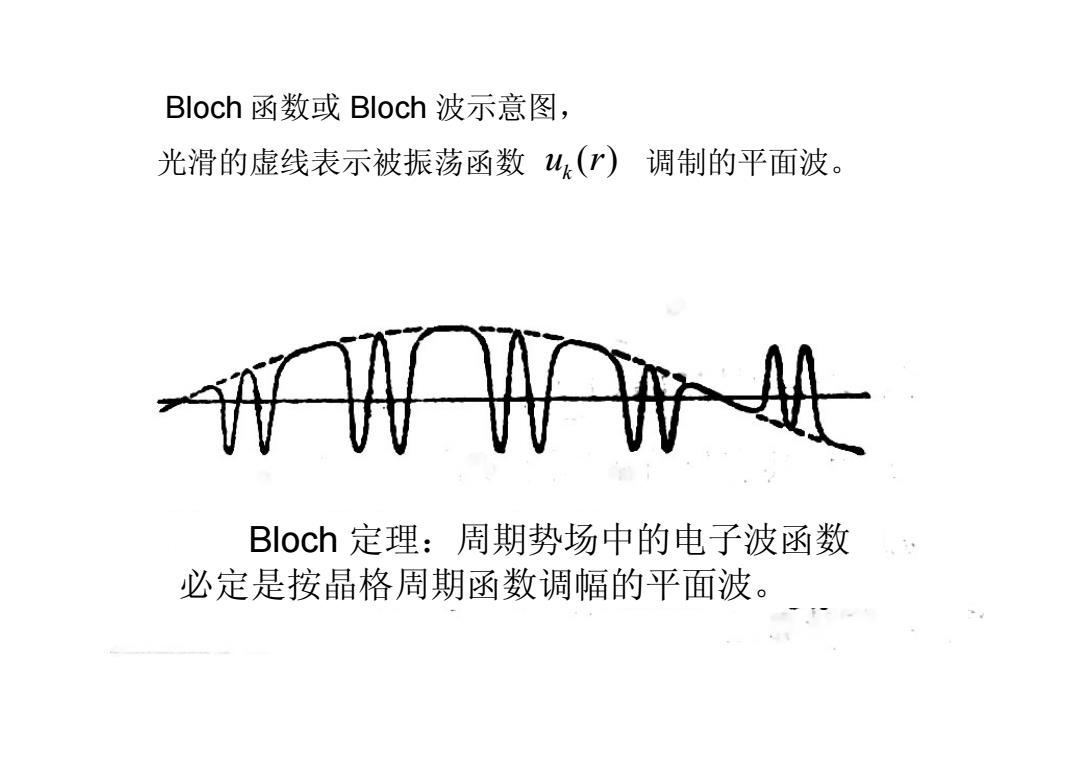
Bloch函数或Bloch波示意图, 光滑的虚线表示被振荡函数u(r)调制的平面波。 Bloch定理:周期势场中的电子波函数 必定是按晶格周期函数调幅的平面波
Bloch 定理:周期势场中的电子波函数 必定是按晶格周期函数调幅的平面波。 Bloch 函数或 Bloch 波示意图, 光滑的虚线表示被振荡函数 u r k ( ) 调制的平面波
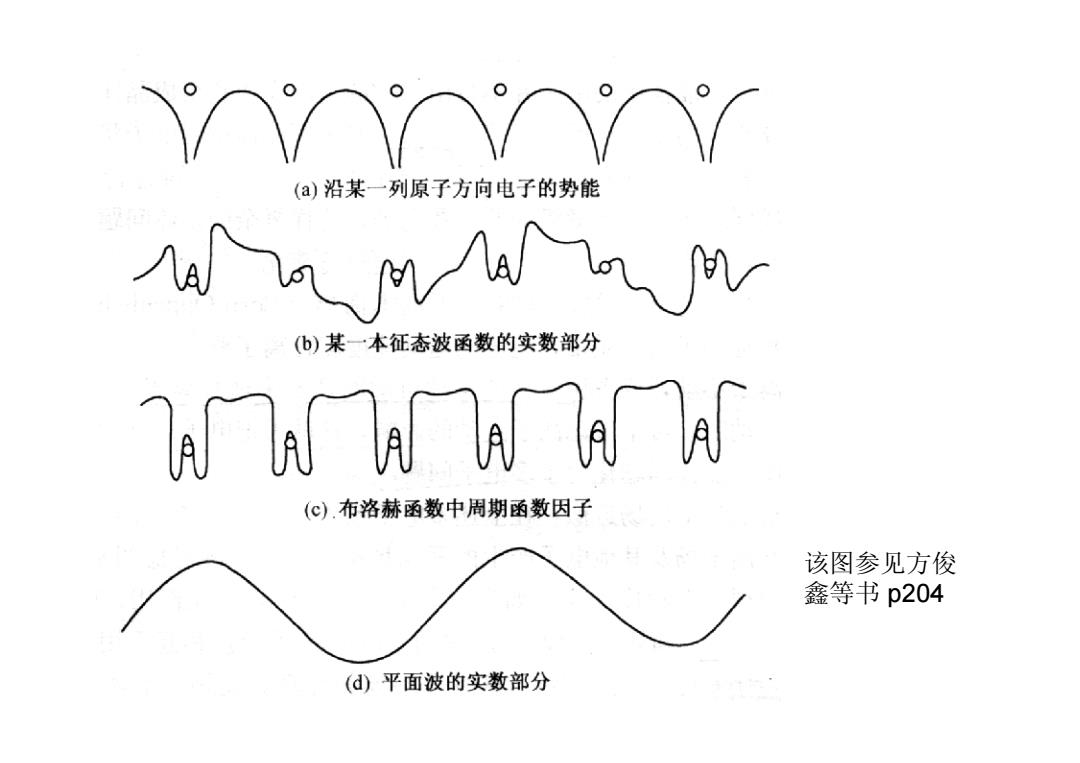
M (a)沿某一列原子方向电子的势能 aL九a^Jv (b)某一本征态波函数的实数部分 h n h Th in h (c).布洛赫函数中周期函数因子 该图参见方俊 鑫等书p204 (d)平面波的实数部分
该图参见方俊 鑫等书 p204

B引och定理的物理证明: 周期势场中的波函数也应具有周期性是无疑的,因此方程 的解可以表示为:必k(r)=f(r)u,(r)其中x(r+Rn)=(r) 势场的周期性也使与电子相关的所有可测量,包括电子几率 w(r)也必定是周期性的,这就给未知函数f(r)附加了下述 条件:fr+R)2=fr) 对于所有R,都满足此条件的函数只能是指数形式:ekr 因此运动方程的解具有Bloch形式: yk(r)=ekr(r) 见冯端:凝聚态物理学(上)p141
Bloch 定理的物理证明: 周期势场中的波函数也应具有周期性是无疑的,因此方程 的解可以表示为: 其中 势场的周期性也使与电子相关的所有可测量,包括电子几率 也必定是周期性的,这就给未知函数 附加了下述 条件: ( ) ( ) ( ) k k y r = f r u r 2 y ( )r f r( ) 2 2 ( ) ( ) n f r + = R f r 对于所有 都满足此条件的函数只能是指数形式: 因此运动方程的解具有Bloch 形式: R n ik r e × ( ) ( ) k n k u r + = R u r ( ) ( ) i y e u × k k = k r r r 见冯端:凝聚态物理学(上)p141