
从以上讨论中,可以看到能带论是在三个近似下完成的: Born一Oppenheimer绝热近似: Hatree一Fock平均场近似 周期场近似(Periodic potential approximation): 每个电子都在完全相同的严格周期性势场中运动,因此每 个电子的运动都可以单独考虑。 所以,能带论是单电子近似的理论。尽管能带论经常 处理的是多电子问题,但是,多电子是填充在由单电子处 理得到的能带上。可以这样做的原因就在于单电子近似, 即每个电子可以单独处理。用这种方法求出的电子能量状 态将不再是分立的能级,而是由能量上可以填充的部分 (允带)和禁止填充的部分(禁带)相间组成的能带,所 以这种理论称为能带论
从以上讨论中,可以看到能带论是在三个近似下完成的: Born-Oppenheimer 绝热近似: Hatree-Fock 平均场近似 周期场近似(Periodic potential approximation): 每个电子都在完全相同的严格周期性势场中运动,因此每 个电子的运动都可以单独考虑。 所以,能带论是单电子近似的理论。尽管能带论经常 处理的是多电子问题,但是,多电子是填充在由单电子处 理得到的能带上。可以这样做的原因就在于单电子近似, 即每个电子可以单独处理。用这种方法求出的电子能量状 态将不再是分立的能级,而是由能量上可以填充的部分 (允带)和禁止填充的部分(禁带)相间组成的能带,所 以这种理论称为能带论
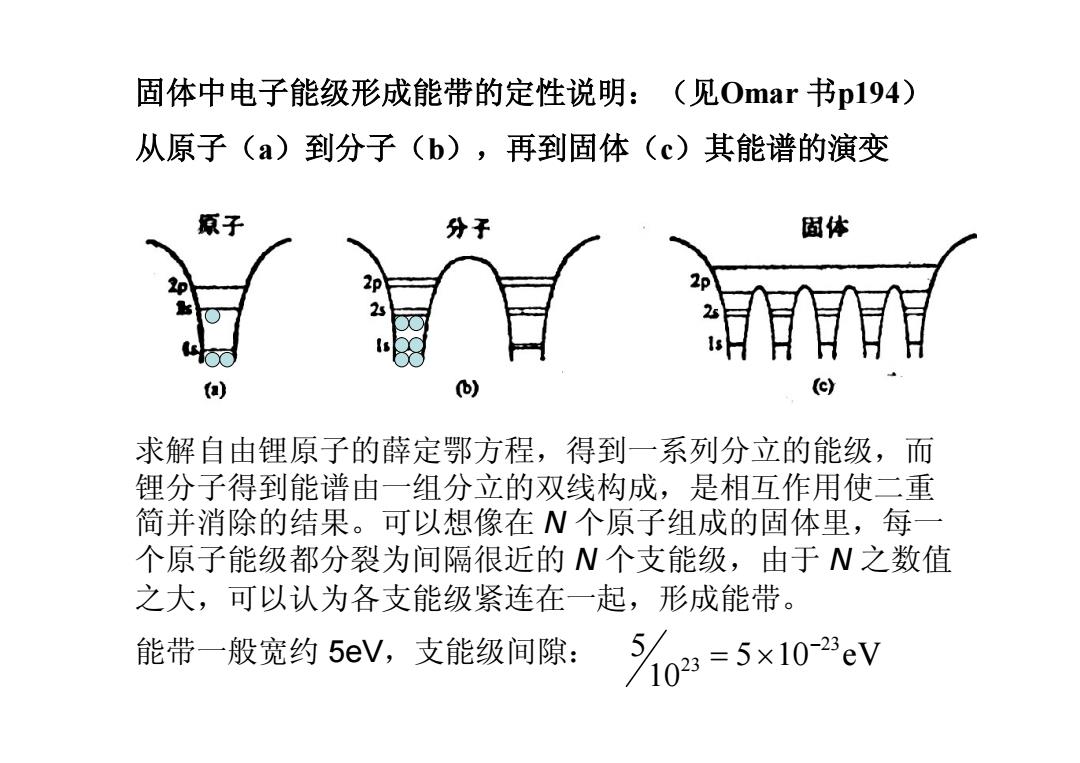
固体中电子能级形成能带的定性说明:(见0mar书p194) 从原子(a)到分子(b),再到固体(c)其能谱的演变 原子 分子 固体 2 25 ( 求解自由锂原子的薛定鄂方程,得到一系列分立的能级,而 锂分子得到能谱由一组分立的双线构成,是相互作用使二重 简并消除的结果。可以想像在N个原子组成的固体里,每一 个原子能级都分裂为间隔很近的N个支能级,由于N之数值 之大,可以认为各支能级紧连在一起,形成能带。 能带一般宽约5eV,支能级间隙:0=5x105cV
固体中电子能级形成能带的定性说明:(见Omar 书p194) 从原子(a)到分子(b),再到固体(c)其能谱的演变 求解自由锂原子的薛定鄂方程,得到一系列分立的能级,而 锂分子得到能谱由一组分立的双线构成,是相互作用使二重 简并消除的结果。可以想像在 N 个原子组成的固体里,每一 个原子能级都分裂为间隔很近的 N 个支能级,由于 N 之数值 之大,可以认为各支能级紧连在一起,形成能带。 能带一般宽约 5eV,支能级间隙: 23 23 5 5 10 eV 10 - = ´

需要指出的是: 在固体物理中,能带论是从周期性势场中推导出来的,这 是由于人们对固体性质的研究首先是从晶态固体开始的。而周 期性势场的引入也使问题得到简化,从而使理论计算得以顺利 进行。所以,传统固体物理一直以晶态固体为主要研究对象。 然而,周期性势场并不是电子具有能带结构的必要条件,现已 证实,在非晶固体中,电子同样有能带结构。 电子能带的形成是由于当原子与原子结合成固体时,原子 之间存在相互作用的结果,而并不取决于原子聚集在一起是晶 态还是非晶态,即原子的排列是否具有平移对称性并不是形成 能带的必要条件,只是给我们的理论计算带来方便,使我们找 到一个捷径、一个突破口,首先解释了晶体问题
需要指出的是: 在固体物理中,能带论是从周期性势场中推导出来的,这 是由于人们对固体性质的研究首先是从晶态固体开始的。而周 期性势场的引入也使问题得到简化,从而使理论计算得以顺利 进行。所以,传统固体物理一直以晶态固体为主要研究对象。 然而,周期性势场并不是电子具有能带结构的必要条件,现已 证实,在非晶固体中,电子同样有能带结构。 电子能带的形成是由于当原子与原子结合成固体时,原子 之间存在相互作用的结果,而并不取决于原子聚集在一起是晶 态还是非晶态,即原子的排列是否具有平移对称性并不是形成 能带的必要条件, 只是给我们的理论计算带来方便,使我们找 到一个捷径、一个突破口,首先解释了晶体问题

5.1周期场中单电子状态的一般特征: 一.Bloch定理 二.关于k取值和意义的几点讨论: 三.Bloch函数的性质 黄昆书4.1节p154-157 虽然晶体中电子的运动可以简化成求解周期场作用下 的单电子薛定谔方程,但具体求解仍是困难的,而且不同 晶体中的周期势场的形式和强弱也是不同的,需要针对具 体问题才能进行求解。Bloch首先讨论了在晶体周期场中 运动的单电子波函数应具有的形式,给出了周期场中单电 子状态的一般特征,这对于理解晶体中的电子,求解具体 问题有着指导意义
5.1 周期场中单电子状态的一般特征: 虽然晶体中电子的运动可以简化成求解周期场作用下 的单电子薛定谔方程,但具体求解仍是困难的,而且不同 晶体中的周期势场的形式和强弱也是不同的,需要针对具 体问题才能进行求解。Bloch首先讨论了在晶体周期场中 运动的单电子波函数应具有的形式,给出了周期场中单电 子状态的一般特征,这对于理解晶体中的电子,求解具体 问题有着指导意义。 黄昆 书 4.1节 p154-157 一.Bloch 定理 二.关于 k 取值和意义的几点讨论: 三. Bloch函数的性质

当我开始思考这个问题时,感觉到问题的关键是 解释电子将如何“偷偷地潜行”于金属中的所有离子之 间。…经过简明而直观的傅立叶分析,令我高兴地 发现,这种不同于自由电子平面波的波仅仅借助于一 种周期性调制就可以获得。 F Bloch 一.Bloch定理 考虑一理想完整晶体,所有的原子实都周期性地静 止排列在其平衡位置上,每一个电子都处在除其自身外 其它电子的平均势场和原子实的势场中运动。按照周期 场近似,电子所感受到的势场具有周期性。这样的模型 称为周期场模型
一. Bloch定理 考虑一理想完整晶体,所有的原子实都周期性地静 止排列在其平衡位置上,每一个电子都处在除其自身外 其它电子的平均势场和原子实的势场中运动。按照周期 场近似,电子所感受到的势场具有周期性。这样的模型 称为周期场模型。 当我开始思考这个问题时,感觉到问题的关键是 解释电子将如何“偷偷地潜行”于金属中的所有离子之 间。……. 经过简明而直观的傅立叶分析,令我高兴地 发现,这种不同于自由电子平面波的波仅仅借助于一 种周期性调制就可以获得。 ——F Bloch