
微训练(1)若y与x之间的一组数据为 导航 3 4 6 则y关于x的经验回归直线一定经过的点是 答案:(2,4) 解析:由表中数据得x= 0+1+2+3+4=2, 5= 1+3+5+5+6 4. 5 5 因为经验回归直线必过样本,点的中心亿,习, 所以y关于x的经验回归直线一定经过的点是(2,4)
微训练 导航 (1)若y与x之间的一组数据为 则y关于x的经验回归直线一定经过的点是 . 答案:(2,4) x 0 1 2 3 4 y 1 3 5 5 6 解析:由表中数据得𝒙 = 𝟎+𝟏+𝟐+𝟑+𝟒 𝟓 =2,𝒚 = 𝟏+𝟑+𝟓+𝟓+𝟔 𝟓 =4. 因为经验回归直线必过样本点的中心(𝒙, 𝒚), 所以y关于x的经验回归直线一定经过的点是(2,4)

导 (2)若一组观测值(化1y1),(2y2),…,化yn)之间满足ybx++e (i1,2,,n),且e恒为0,则R2为 答案:1 解标:由台恒为0,知即r90故-=1盛0 n =1-0=1 B0-列2
导航 (2)若一组观测值(x1 ,y1 ),(x2 ,y2 ),…,(xn ,yn )之间满足yi =bxi+a+ei (i=1,2,… ,n),且ei恒为0,则R2为 . 答案:1 解析:由 ei恒为 0,知 yi=𝒚 ^ 𝐢 ,即 yi-𝐲 ^ 𝒊 =0,故 R2 =1- ∑ 𝒊=𝟏 𝒏 (𝒚𝒊 -𝒚 ^ 𝒊 ) 𝟐 ∑ 𝒊=𝟏 𝒏 (𝒚𝒊 -𝒚) 𝟐 =1-0=1

导期 课堂·重难突破 线性回归分析 典例剖析 1某种产品的广告费用支出x(单位:百万元)与销售额(单位: 百万元)之间有如下的对应数据: x/ ()画出散点图; 万元 4 5 6 8 (2)求经验回归方程; y/ 3)试预测广告费用支出为10 万元 30 40 60 50 70 百万元时的销售额
导航 一 线性回归分析 典例剖析 1.某种产品的广告费用支出x(单位:百万元)与销售额y(单位: 百万元)之间有如下的对应数据: (1)画出散点图; (2)求经验回归方程; (3)试预测广告费用支出为10 百万元时的销售额. 课堂·重难突破 x/百 万元 2 4 5 6 8 y/百 万元 30 40 60 50 70
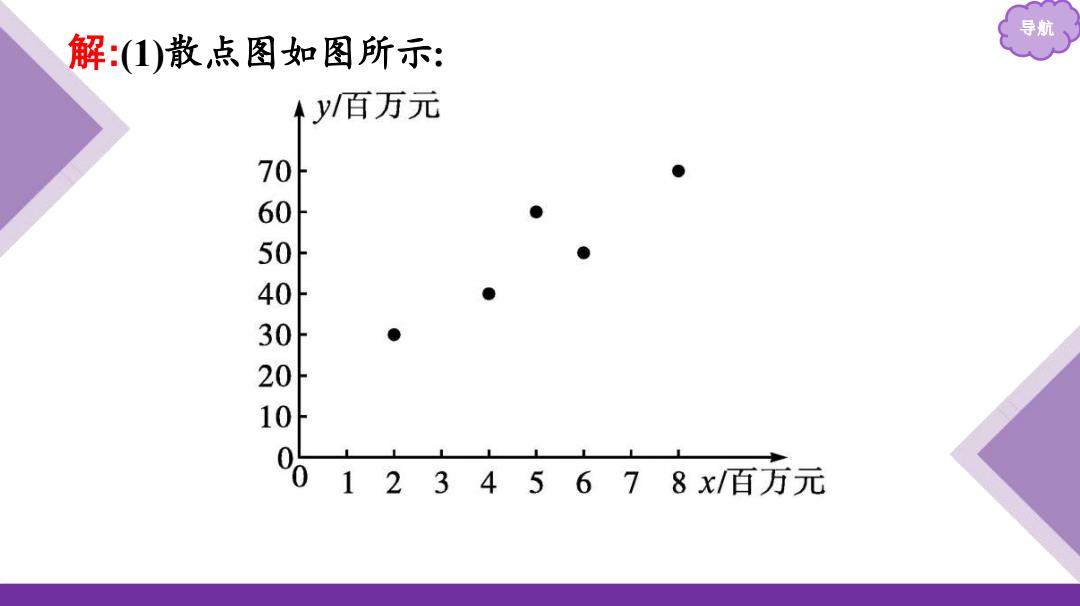
导航 解:1)散点图如图所示: y百万元 ● 00000010 ● 12345678x/百万元
导航 解 :(1)散点图如图所示:

(2)列出下表,并用科学计算器进行有关计算: 导航 2 5 合计 4 5 6 8 25 Yi 30 40 60 50 70 250 计算得x = 5= 50, 250 5 于是可得6=盛0 5 =6.5, 8-2 a=-bx=50-6.5×5=17.5.即经验回归方程为y=6.5x+17.5
导航 (2)列出下表,并用科学计算器进行有关计算: i 1 2 3 4 5 合计 xi 2 4 5 6 8 25 yi 30 40 60 50 70 250 计算得𝒙 = 𝟐 𝟓𝟓 =5, 𝒚 = 𝟐 𝟓 𝟎 𝟓 =50, 于是可得 𝒃^ = ∑𝐢=𝟏𝟓 (𝒙𝒊-𝒙)(𝒚𝒊-𝒚) ∑𝒊=𝟏𝟓 (𝒙𝒊-𝒙)𝟐 = 6.5, 𝒂^ = 𝒚 − 𝒃^ 𝒙 =50-6.5 × 5 =17.5.即经验回归方程为𝒚^ = 6.5x+17.5