
利用边界条件:p=ul=0[C, Ina+C, =U求得C, In b+C, = 0UU ln baaInInbb最后求得6UapeE=ararInb1ou1QuQugradu= Vu=aa-arra0rsin ap球坐标系
利用边界条件: r a U = = r=b = 0 + = + = ln 0 ln 1 2 1 2 C b C C a C U 求得 = b a U C ln 1 = − b a U b C ln ln 2 = b a b r U ln ln = − = − = − b a U r r r r ln e E e 最后求得 + + = = u r a u r a r u gradu u ar sin 1 1 球坐标系

由上例可见,为了利用给定的边界条件以便确定求解过程中出现的积分常数,选择适当的坐标系是非常重要的。此外,由于同轴线中的电位函数仅与一个坐标变量r有关,因此原先的三维拉普拉斯方程简化为一维微分方程,因而可采用直接积分方法求解这类边值问题。一般说来,静电场的边值问题与空间三个坐标变量有关。为了求解三维拉普拉斯方程,一种有效的方法就是分离变量法?分离变量法是将原先的三维偏微分方程通过变量分离简化为三个独立的常微分方程,从而使求解过程比较简便。分离变量法对于11种坐标系都是行之有效的
由上例可见,为了利用给定的边界条件以便确定 求解过程中出现的积分常数,选择适当的坐标系是非 常重要的。 此外,由于同轴线中的电位函数仅与一个坐标变 量 r 有关,因此原先的三维拉普拉斯方程简化为一维 微分方程,因而可采用直接积分方法求解这类边值问 题。 分离变量法是将原先的三维偏微分方程通过变量分 离简化为三个独立的常微分方程,从而使求解过程比较 简便。分离变量法对于11种坐标系都是行之有效的。 一般说来,静电场的边值问题与空间三个坐标变 量有关。为了求解三维拉普拉斯方程,一种有效的方 法就是分离变量法

3-3镜像法实质:是以一个或几个等效电荷代替边界的影响,将原来具有边界的非均匀空间变成无限大的均匀自由空间,从而使计算过程大为简化。这些等效电荷通常处于原电荷的镜像位置,因此称为镜像电荷,而这种方法称为镜像法依据:惟一性定理。等效电荷的引入不能改变原来的边界条件。关键:确定镜像电荷的大小及其位置。局限性:仅仅对于某些特殊的边界以及特殊的电荷分布才有可能确定其镜像电荷
3-3 镜像法 实质: 是以一个或几个等效电荷代替边界的影响, 将原来具有边界的非均匀空间变成无限大的均匀自由空 间,从而使计算过程大为简化。 依据:惟一性定理。等效电荷的引入不能改变原来的 边界条件。 关键:确定镜像电荷的大小及其位置。 局限性:仅仅对于某些特殊的边界以及特殊的电荷 分布才有可能确定其镜像电荷。 这些等效电荷通常处于原电荷的镜像位置,因此称为 镜像电荷,而这种方法称为镜像法
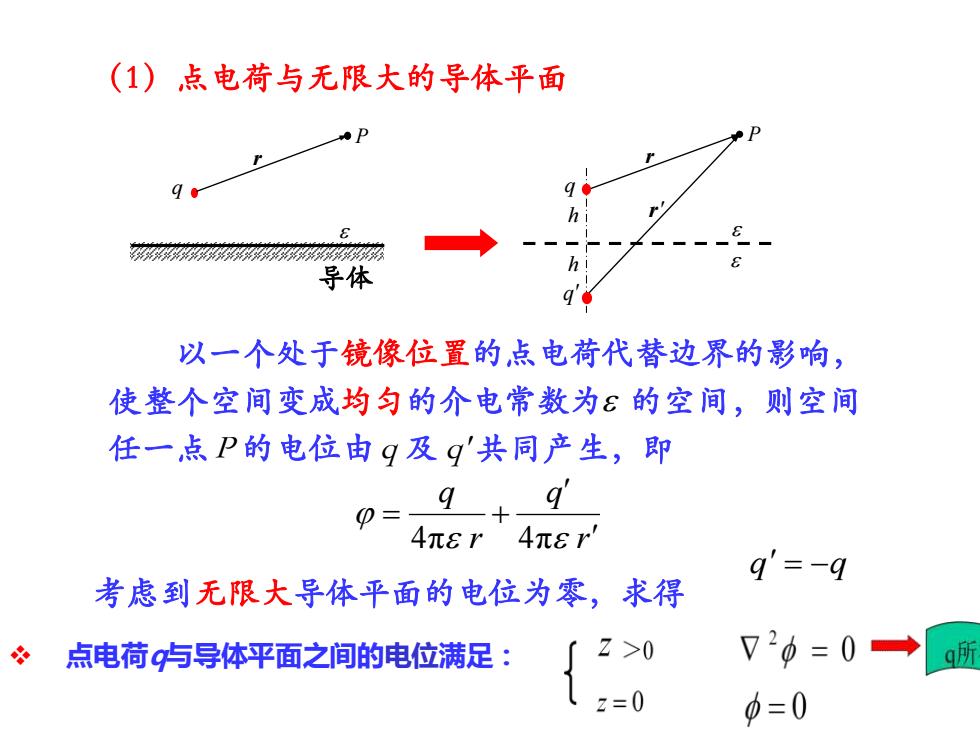
(1)点电荷与无限大的导体平面qh813666995699555955956959999669563h导体q以一个处于镜像位置的点电荷代替边界的影响,使整个空间变成均匀的介电常数为8的空间,则空间任一点P的电位由q及q共同产生,即q'9P:4元r4元8q'=-q考虑到无限大导体平面的电位为零,求得V?0=0Z >0g所点电荷9与导体平面之间的电位满足:z=0Φ=0
(1)点电荷与无限大的导体平面 导体 q r P q r P h h r q 以一个处于镜像位置的点电荷代替边界的影响, 使整个空间变成均匀的介电常数为 的空间,则空间 任一点 P 的电位由q 及 q' 共同产生,即 r q r q = + 4π 4π 考虑到无限大导体平面的电位为零,求得 q = −q ❖ 点电荷q与导体平面之间的电位满足:
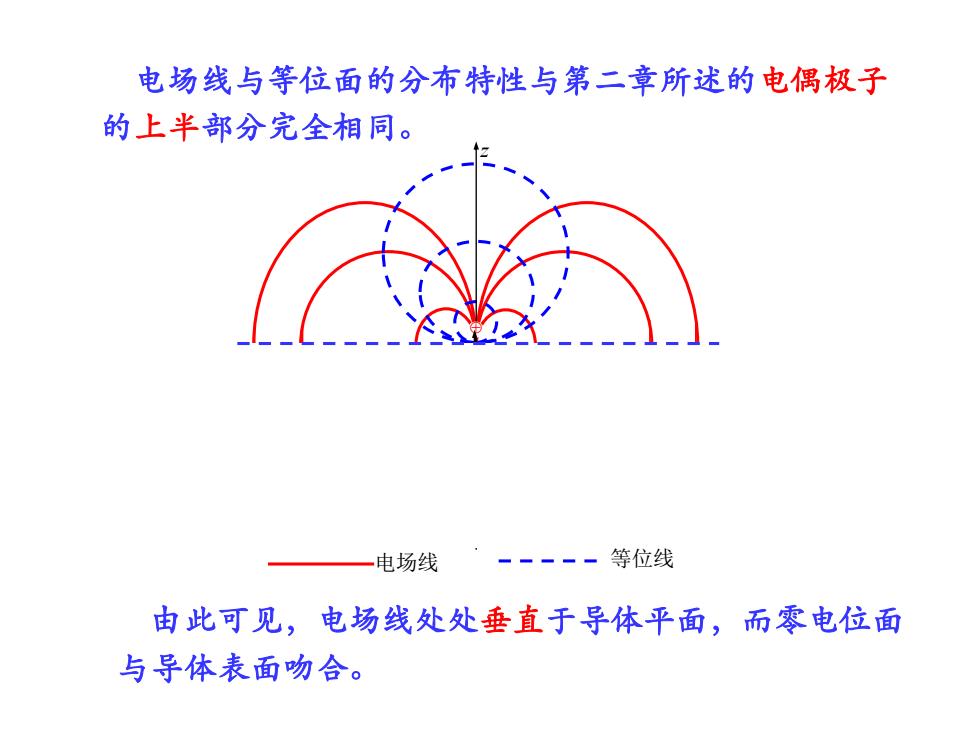
电场线与等位面的分布特性与第二章所述的电偶极子的上半部分完全相同。等位线电场线由此可见,电场线处处垂直于导体平面,而零电位面与导体表面吻合
电场线与等位面的分布特性与第二章所述的电偶极子 的上半部分完全相同。 由此可见,电场线处处垂直于导体平面,而零电位面 与导体表面吻合。 电场线 等位线 z