例题2-1已知F=10kN;F=20kN;13F=35kN:F=25kN:试画出图示杆件的轴力图13解:1、计算各段的轴力。FNZF=0AB段Fw =F =10kNN2ZF=0FN2+F=FBC段FN2EF-F=FN310-20=-10kN25ZF=0CD段F (kN)10Fna =F =25kNX2、绘制轴力图10
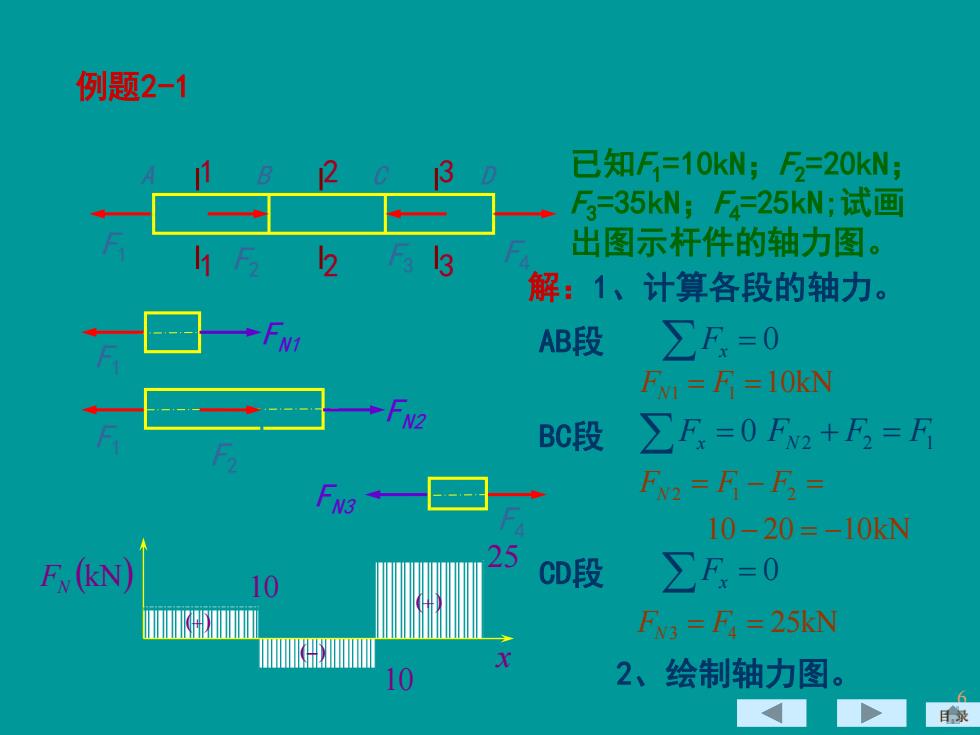
6 已知F1=10kN;F2=20kN; F3=35kN;F4=25kN;试画 出图示杆件的轴力图。 1 1 Fx = 0 FN1 = F1 =10kN 例题2-1 解:1、计算各段的轴力。 AB段 10 20 10kN 2 1 2 − = − FN = F − F = BC段 2 2 3 3 FN2 F1 F2 Fx = 0 FN2 + F2 = F1 Fx = 0 FN3 = F4 = 25kN CD段 2、绘制轴力图。 (kN) FN x 10 25 10 (+) (−) (+) 目 录 F1 F2 F3 F4 A B C D FN1 F1 FN3 F4

讨论题以下关于轴力的说法中,哪一个是错误的拉压杆的内力只有轴力;AOB轴力的作用线与杆轴重合;轴力是沿杆轴作用的外力;C轴力与杆的横截面和材料无关D目录
7 目 录

2、横截面上的应力杆件1轴力=1N,截面积=0.1cm杆件2—轴力=100N,截面积=100cm2哪个杆工作“累”?应力不能只看轴力,要看单位面积上的力怎样求出应力?(内力集度)思路应力是内力延伸出的概念,应当由内力一→应力
8 2 、 横截面上的应力 杆件1 —— 轴力 = 1N, 截面积 = 0.1 cm2 杆件2 —— 轴力 = 100N, 截面积 = 100 cm2 哪个杆工作“累”? 不能只看轴力,要看单位面积上的力—— 应力 • 怎样求出应力?(内力集度) 思路——应力是内力延伸出的概念,应当由 内力 应力

1)静力平衡由 dN=dA积分得N=[odA截面各点应力的分布?因不知道,故上式求不出应力要想另外的办法
9 由 dN = dA 积分得 = A N d A 1)静力平衡 截面各点应力的分布? 因不知道,故 上式求不出应力 要想另外的办法 F

baFEab2)几何变形ddC实验结果变形后,外表面垂线保持为直线平面假设一变形后,截面平面仍垂直于杆轴推得:同一横截面上各点的正应力?相等,即正应力均匀分布于横截面上,等于常量。于是有:N=[dA=O dA=OAtN得应力:0=FNA10
10 2)几何变形 实验结果——变形后,外表面垂线保持为直线 平面假设——变形后,截面平面仍垂直于杆轴 推得:同一横截面上各点的正应力σ相等,即正应 力均匀分布于横截面上,σ等于常量。于是有: 得应力: N A A A A A = d = d = A N = a b F a` b ` F c ` d ` c d F FN σ