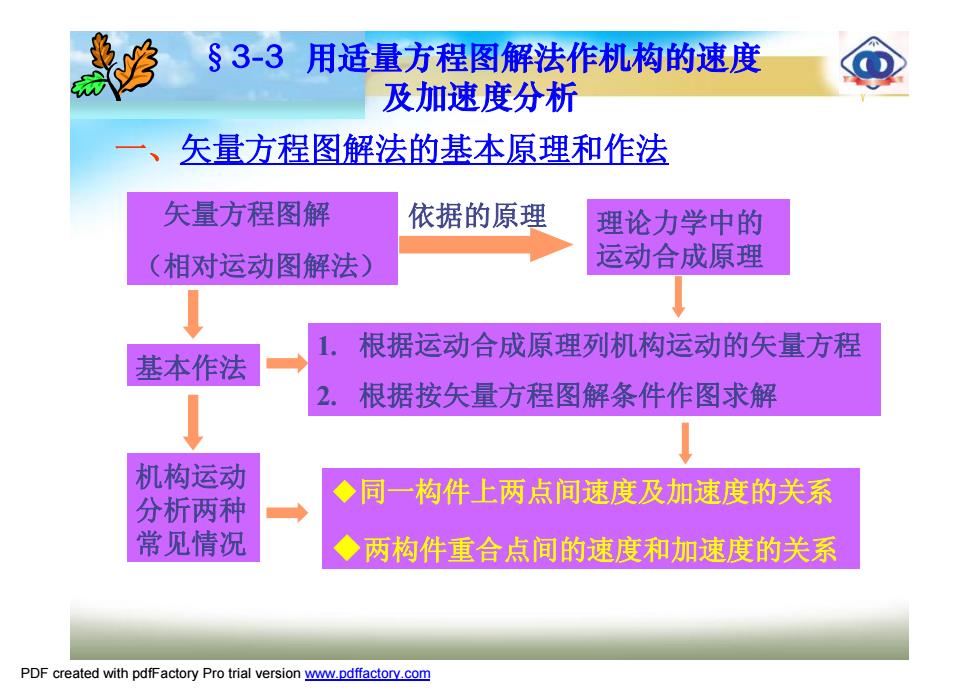
§3-3用适量方程图解法作机构的速度 及加速度分析 矢量方程图解法的基本原理和作法 矢量方程图解 依据的原理 理论力学中的 (相对运动图解法) 运动合成原理 根据运动合成原理列机构运动的矢量方程 基本作法 根据按矢量方程图解条件作图求解 机构运动 ◆同一构件上两点间速度及加速度的关系 分析两种 常见情况 ◆两构件重合点间的速度和加速度的关系 PDF created with pdfFactory Pro trial version www.pdffactory.com
§3-3 用适量方程图解法作机构的速度 及加速度分析 一、矢量方程图解法的基本原理和作法 矢量方程图解 (相对运动图解法) 依据的原理 理论力学中的 运动合成原理 1. 根据运动合成原理列机构运动的矢量方程 2. 根据按矢量方程图解条件作图求解 基本作法 ◆同一构件上两点间速度及加速度的关系 ◆两构件重合点间的速度和加速度的关系 机构运动 分析两种 常见情况 PDF created with pdfFactory Pro trial version www.pdffactory.com
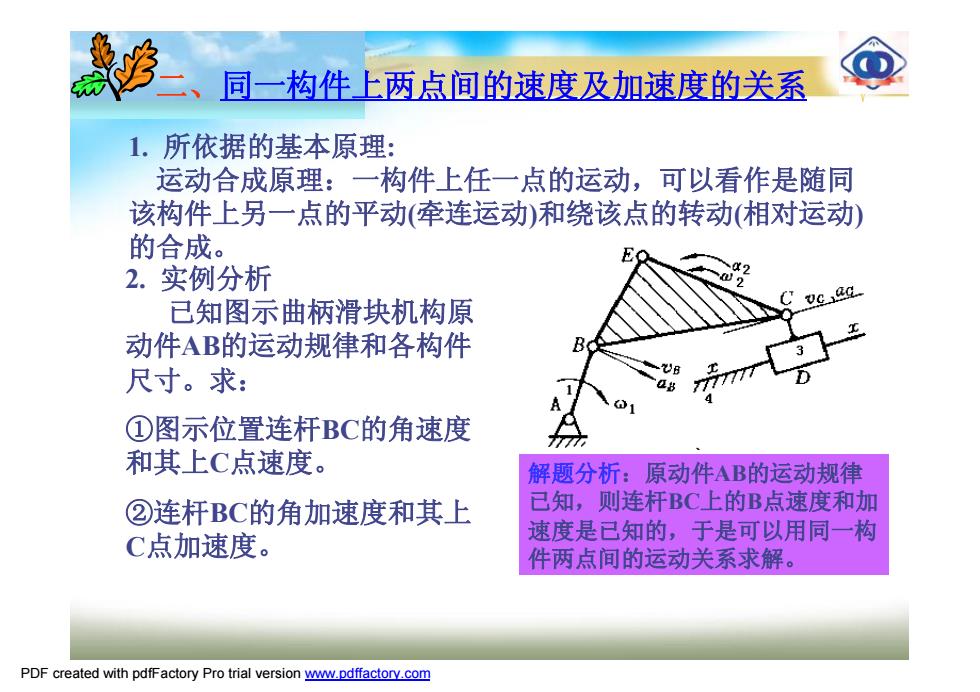
惑多、目—构件上两点间的速度及加速度的关系 1. 所依据的基本原理: 运动合成原理:一构件上任一点的运动,可以看作是随同 该构件上另一点的平动(牵连运动)和绕该点的转动(相对运动) 的合成。 E 2.实例分析 已知图示曲柄滑块机构原 动件AB的运动规律和各构件 尺寸。求: ①图示位置连杆BC的角速度 和其上C点速度。 解题分析:原动件AB的运动规律 ②连杆BC的角加速度和其上 已知,则连杆BC上的B点速度和加 C点加速度。 速度是已知的,于是可以用同一构 件两点间的运动关系求解。 PDF created with pdfFactory Pro trial version www.pdffactory.com
二、同一构件上两点间的速度及加速度的关系 1. 所依据的基本原理: 运动合成原理:一构件上任一点的运动,可以看作是随同 该构件上另一点的平动(牵连运动)和绕该点的转动(相对运动) 的合成。 2. 实例分析 已知图示曲柄滑块机构原 动件AB的运动规律和各构件 尺寸。求: ①图示位置连杆BC的角速度 和其上C点速度。 ②连杆BC的角加速度和其上 C点加速度。 解题分析:原动件AB的运动规律 已知,则连杆BC上的B点速度和加 速度是已知的,于是可以用同一构 件两点间的运动关系求解。 PDF created with pdfFactory Pro trial version www.pdffactory.com
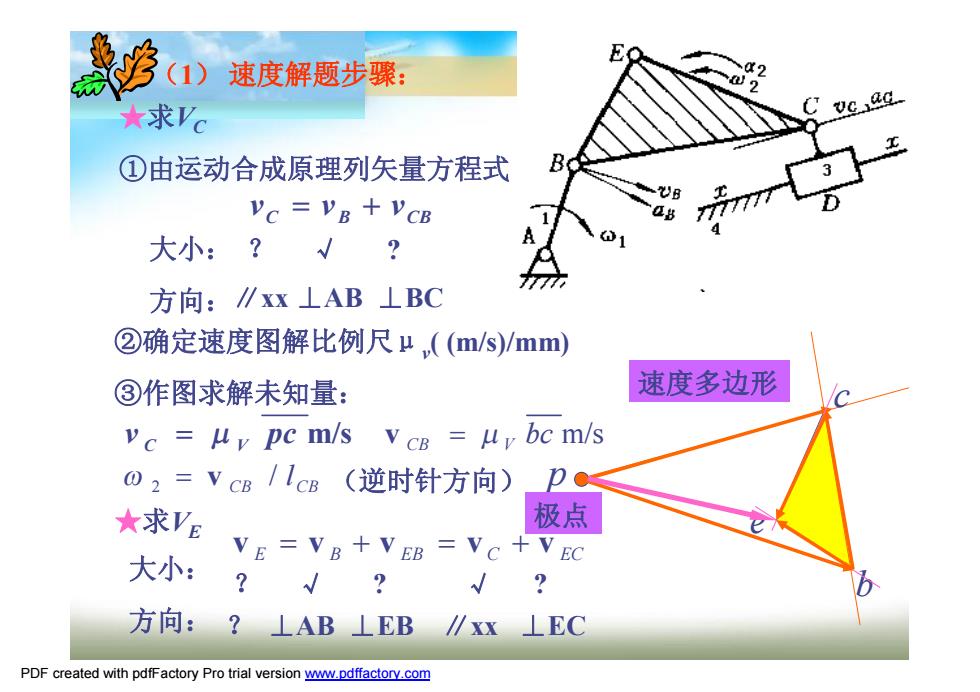
速度解题步骤: ★求' vc ag ①由运动合成原理列矢量方程式 VC VB+VCB 大小:?√ 方向:∥xx⊥AB⊥BC ②确定速度图解比例尺μ((m/s)/mm) ③作图求解未知量: 速度多边形 vc=uy pc m/s V CB uv bc m/s O2=vcB/IcB(逆时针方向) ★求VE 极点 VE=VB+VEB -VC+VEC 大小: √ 2 方向:?⊥AB⊥EB ∥xx⊥EC PDF created with pdfFactory Pro trial version www.pdffactory.com
C B CB v = v + v (1) 速度解题步骤: 大小: 方向: ? √ ? ∥xx ⊥AB ⊥BC c p b e ②确定速度图解比例尺μv ( (m/s)/mm) ③作图求解未知量: v pc m/s C = m V bc m/s CB = m V v v E = v B + v EB = v C + v EC CB CB / l 2 w = v (逆时针方向) ★求VE 大小: 方向: ? √ ? ? ⊥AB ⊥EB ∥xx ⊥EC √ ? 速度多边形 极点 ★求VC ①由运动合成原理列矢量方程式 PDF created with pdfFactory Pro trial version www.pdffactory.com
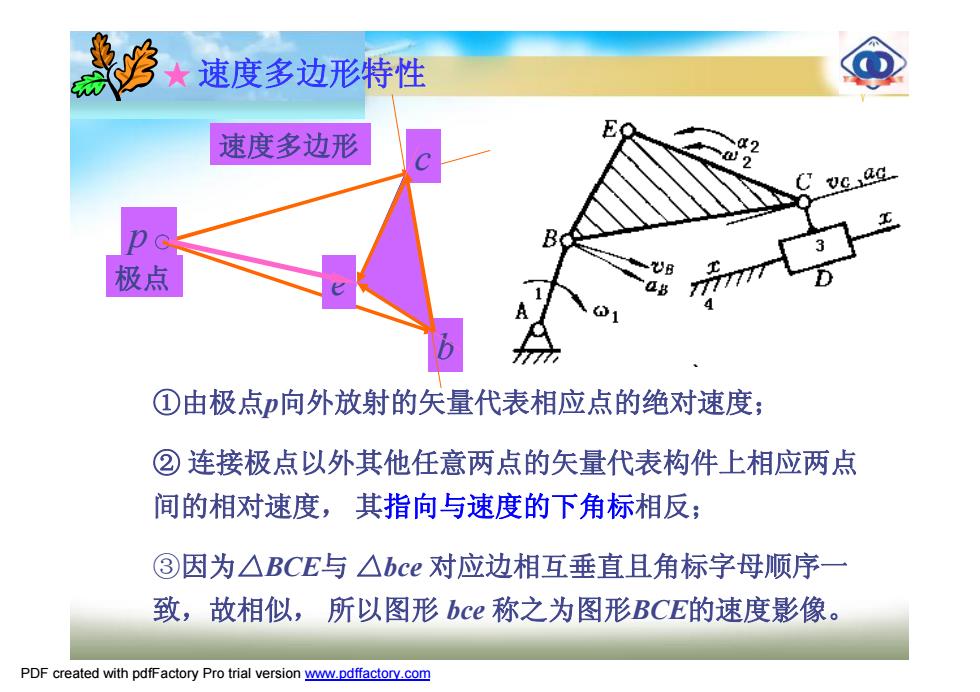
★速度多边形特性 速度多边形 极点 ①由极点向外放射的矢量代表相应点的绝对速度; ②连接极点以外其他任意两点的矢量代表构件上相应两点 间的相对速度,其指向与速度的下角标相反; ③因为△BCE与△bce对应边相互垂直且角标字母顺序一 致,故相似,所以图形bce称之为图形BCE的速度影像。 PDF created with pdfFactory Pro trial version www.pdffactory.com
①由极点p向外放射的矢量代表相应点的绝对速度; ② 连接极点以外其他任意两点的矢量代表构件上相应两点 间的相对速度, 其指向与速度的下角标相反; ③因为△BCE与 △bce 对应边相互垂直且角标字母顺序一 致,故相似, 所以图形 bce 称之为图形BCE的速度影像。 c p b e 速度多边形 极点 ★ 速度多边形特性 PDF created with pdfFactory Pro trial version www.pdffactory.com