1、DF检验(Dicky-Fuller Test) X,=X+4, 随机游走,非平稳 对该式回归,如果确实 X,=pX-+4, 发现p=1,则称随机变 量Xt有一个单位根。 △X,=(p-1)X1+4, 等价于通过该式判断 =δX-1+4, 是否存在δ=0。 。 通过上式判断Xt是否有单位根,就是时间序列 平稳性的单位根检验
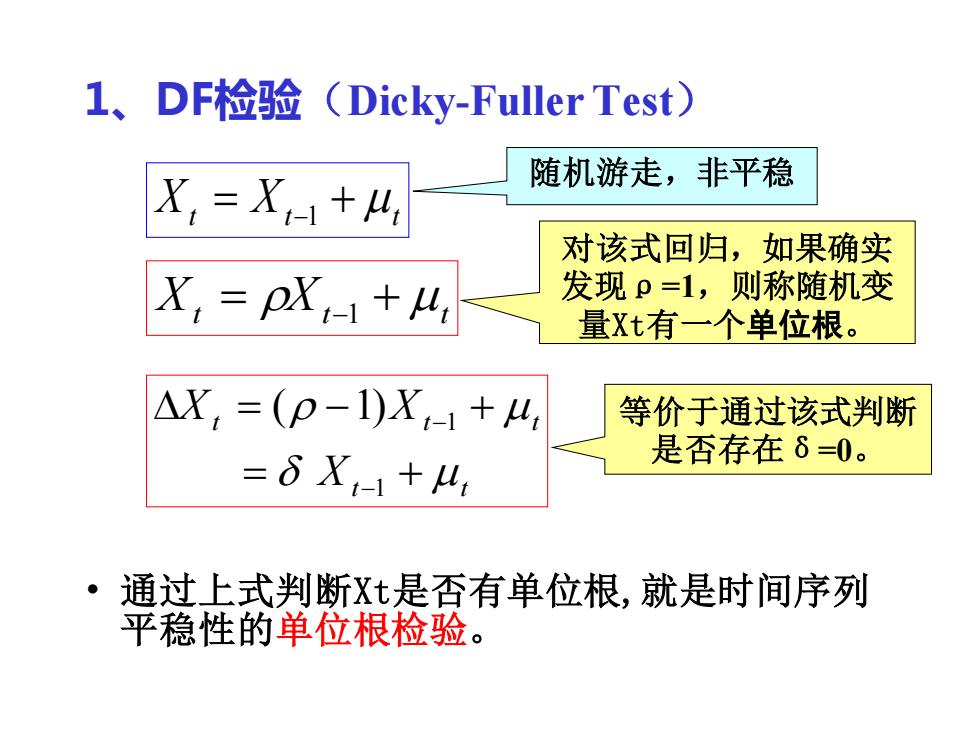
1、DF检验(Dicky-Fuller Test) • 通过上式判断Xt是否有单位根,就是时间序列 平稳性的单位根检验。 Xt = Xt−1 + t Xt = Xt−1 + t t t t t t X X X = + = − + − − 1 1 ( 1) 随机游走,非平稳 对该式回归,如果确实 发现ρ=1,则称随机变 量Xt有一个单位根。 等价于通过该式判断 是否存在δ=0

·一般检验模型 X=a+pX+u △X,=C+X-1+4, 零假设 H0:6=0 备择假设H1:δ<0 可通过OLS法下的检验完成
• 一般检验模型 Xt = + Xt−1 + t Xt = +Xt−1 + t 零假设 H0:=0 备择假设 H1:<0 可通过OLS法下的t检验完成

·但是,在零假设(序列非平稳)下,即使在大样 本下统计量也是有偏误的(向下偏倚),通常的 t检验无法使用。 ·Dicky和Fuller-于1976年提出了这一情形下t统计 量服从的分布(这时的统计量称为τ统计量), 即DF分布。 ·由于统计量的向下偏倚性,它呈现围绕小于零均 值的偏态分布
• 但是,在零假设(序列非平稳)下,即使在大样 本下t统计量也是有偏误的(向下偏倚),通常的 t 检验无法使用。 • Dicky和Fuller于1976年提出了这一情形下t统计 量服从的分布(这时的t统计量称为统计量), 即DF分布。 • 由于t统计量的向下偏倚性,它呈现围绕小于零均 值的偏态分布

样本容量 显著性水平 25 50 100 500 分布临界值 (n=) 0.01 -3.75 -3.58 -3.51 -3.44 -3.43 -2.33 0.05 -3.00 -2.93 -2.89 -2.87 -2.86 -1.65 0.10 -2.63-2.60 -2.58 -2.57 -2.57 -1.28 如果长临界值,则拒绝零假设Ho:δ=0,认为 时间序列不存在单位根,是平稳的。 单尾检验
• 如果t<临界值,则拒绝零假设H0: =0,认为 时间序列不存在单位根,是平稳的。 单尾检验 样 本 容 量 显著性水平 25 50 100 500 ∝ t分布临界值 (n=∝) 0.01 -3.75 -3.58 -3.51 -3.44 -3.43 -2.33 0.05 -3.00 -2.93 -2.89 -2.87 -2.86 -1.65 0.10 -2.63 -2.60 -2.58 -2.57 -2.57 -1.28

2、ADF检验(Augment Dickey-Fuller test) ·为什么将DF检验扩展为ADF检验? DF检验假定时间序列是由具有白噪声随机误差 项的一阶自回归过程AR1)生成的。但在实际检 验中,时间序列可能由更高阶的自回归过程生 成,或者随机误差项并非是白噪声,用OLS法 进行估计均会表现出随机误差项出现自相关, 导致DF检验无效。 ·如果时间序列含有明显的随时间变化的某种趋 势(如上升或下降),也容易导致DF检验中的 自相关随机误差项问题
2、ADF检验(Augment Dickey-Fuller test) • 为什么将DF检验扩展为ADF检验? • DF检验假定时间序列是由具有白噪声随机误差 项的一阶自回归过程AR(1)生成的。但在实际检 验中,时间序列可能由更高阶的自回归过程生 成,或者随机误差项并非是白噪声,用OLS法 进行估计均会表现出随机误差项出现自相关, 导致DF检验无效。 • 如果时间序列含有明显的随时间变化的某种趋 势(如上升或下降),也容易导致DF检验中的 自相关随机误差项问题