
·ADF检验模型 AX,8X+2 BAX+5 模型1 i=1 △X,=u+X,-1+∑B,AX-,+8 模型2 i=1 △X,=a+Bm+Y,1+∑B,AX,-+s 模型3 i=1 零假设 H0:δ=0 备择假设H1:6<0
• ADF检验模型 t m i Xt Xt i Xt i = + + = − − 1 1 t m i Xt Xt i Xt i = + + + = − − 1 1 t m i t Xt i Xt i X = + t + + + = − − 1 1 零假设 H0:=0 备择假设 H1:<0 模型1 模型2 模型3

·检验过程 -实际检验时从模型3开始,然后模型2、模型1。 -何时检验拒绝零假设,即原序列不存在单位根,为 平稳序列,何时停止检验。 -否则,就要继续检验,直到检验完模型1为止。 ·检验原理与DF检验相同,只是对模型1、2、3 进行检验时,有各自相应的临界值表。 ·检验模型滞后项阶数的确定:以随机项不存在 序列相关为准则
• 检验过程 –实际检验时从模型3开始,然后模型2、模型1。 –何时检验拒绝零假设,即原序列不存在单位根,为 平稳序列,何时停止检验。 –否则,就要继续检验,直到检验完模型1为止。 • 检验原理与DF检验相同,只是对模型1、2、3 进行检验时,有各自相应的临界值表。 • 检验模型滞后项阶数的确定:以随机项不存在 序列相关为准则
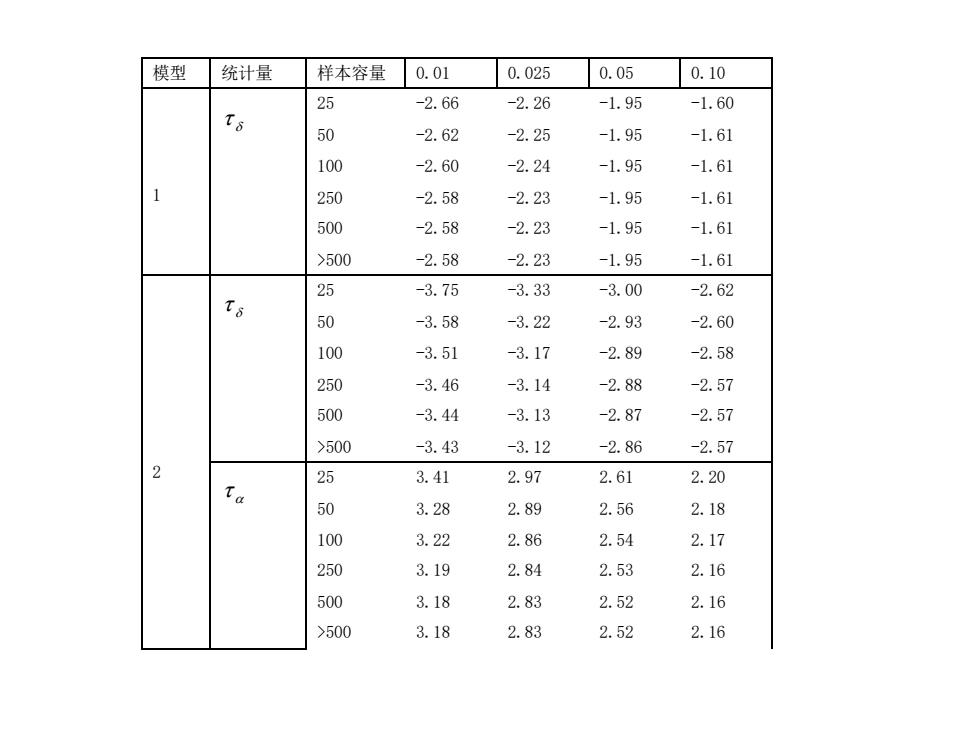
模型 统计量 样本容量 0.01 0.025 0.05 0.10 25 -2.66 -2.26 -1.95 -1.60 0 -2.62 -2.25 -1.95 -1.61 100 -2.60 -2.24 -1.95 -1.61 1 250 -2.58 -2.23 -1.95 -1.61 500 -2.58 -2.23 -1.95 -1.61 >500 -2.58 -2.23 -1.95 -1.61 25 人6 -3.75 -3.33 -3.00 -2.62 50 -3.58 -3.22 -2.93 -2.60 100 -3.51 -3.17 -2.89 -2.58 250 -3.46 -3.14 -2.88 -2.57 500 -3.44 -3.13 -2.87 -2.57 >500 -3.43 -3.12 -2.86 -2.57 2 25 3.41 2.97 2.61 2.20 50 3.28 2.89 2.56 2.18 100 3.22 2.86 2.54 2.17 250 3.19 2.84 2.53 2.16 500 3.18 2.83 2.52 2.16 >500 3.18 2.83 2.52 2.16
模型 统计量 样本容量 0.01 0.025 0.05 0.10 25 -2.66 -2.26 -1.95 -1.60 50 -2.62 -2.25 -1.95 -1.61 100 -2.60 -2.24 -1.95 -1.61 250 -2.58 -2.23 -1.95 -1.61 500 -2.58 -2.23 -1.95 -1.61 1 >500 -2.58 -2.23 -1.95 -1.61 25 -3.75 -3.33 -3.00 -2.62 50 -3.58 -3.22 -2.93 -2.60 100 -3.51 -3.17 -2.89 -2.58 250 -3.46 -3.14 -2.88 -2.57 500 -3.44 -3.13 -2.87 -2.57 >500 -3.43 -3.12 -2.86 -2.57 25 3.41 2.97 2.61 2.20 50 3.28 2.89 2.56 2.18 100 3.22 2.86 2.54 2.17 250 3.19 2.84 2.53 2.16 500 3.18 2.83 2.52 2.16 2 >500 3.18 2.83 2.52 2.16