
1.2复数序列 5 元,-π/2≤B≤π/2,则 A= cos a +i sin a cos B sina sin月. -sin a sin B cosa-isina cosB 10 i cos B sin B cos a 01/ +sina -sin B -i cosB E(099A -sinB -i cosB 即A=E cosa+I sina.其中E是恒等矩阵 E2=E,EI=IE=I; 而且容易验证,矩阵I就是2×2矩阵中的“虚单位”, I2=-E 因此,引用例1.1中的结果就可以得到 m/2 B(1()coa ina k=0 【n-)/☒ +I∑ =E cosna+I sin no. 1.2复数序列 按照一定顺序排列的复数 zn=xn+ih,n=1,2,3,., 称为复数序列,记为{ 一个复数序列完全等价于两个实数序列. 聚点给定序列{n},若存在复数z,e>0,恒有无穷多个n满足n-<e, 则称z为{z}的一个聚点(或极限点)

6 第一章复数和复变函数 一个序列可以有不止一个聚点,例如序列 京景景后8月. (1.15) 就有两个聚点,士1. 特别是,对于实数序列工n的聚点(也必然是实数),其中数值最大的,称为 n}的上极限,记为画:而数值最小的,称为{红n}的下极限,记为巴 上面的序列(1.15)中,士1就分别是它的上、下极限. 由序列上(下)极限的定义,不难证明,当xn≥0,n≥0时,有 n工n'h≤xn·四n, (1.16a) nh≥n·细h (1.16b) 有界序列和无界序列给定序列{n},如果M>0,使n,都有<M, 则序列称为有界的:否则就是无界的 波尔查诺外尔斯特拉斯定理一个有界的无穷序列至少有一个聚点。 极限给定序列{an},如果存在复数z,e>0,N(e)>0,使当n>N(e) 时,有|n-<c,则称{2n}收敛于z,记为 lim in =2. 一个序列的极限必然是此序列的聚点,而且是唯一的聚点. 序列极限存在(序列收敛)的柯西充要条件e>0,3正整数N(),使对于 任意正整数p,有 |2N+p-2N<e. 一个无界序列不可能是收敛的. 1.3复变函数 本节讨论定义在复数平面上的一定区域内的复变函数 为了建立区域的概念,先要定义点集的内点. 如果以某一点为圆心作一个圆,只要半径足够小,使得圆内的所有的点都属 于该点集,则称此点为点集的内点。 区域是满足下列两个条件的点集:(1)全部都由内点组成:(②)具有连通性,即 点集中任意两点,都可以用一条折线连接起来,折线上的点全都属于此点集。 图1.3(a)和(b)中的图形都是区域,但(c)不构成区域. 按照连通性质的不同,还可以将区域分为两类,即
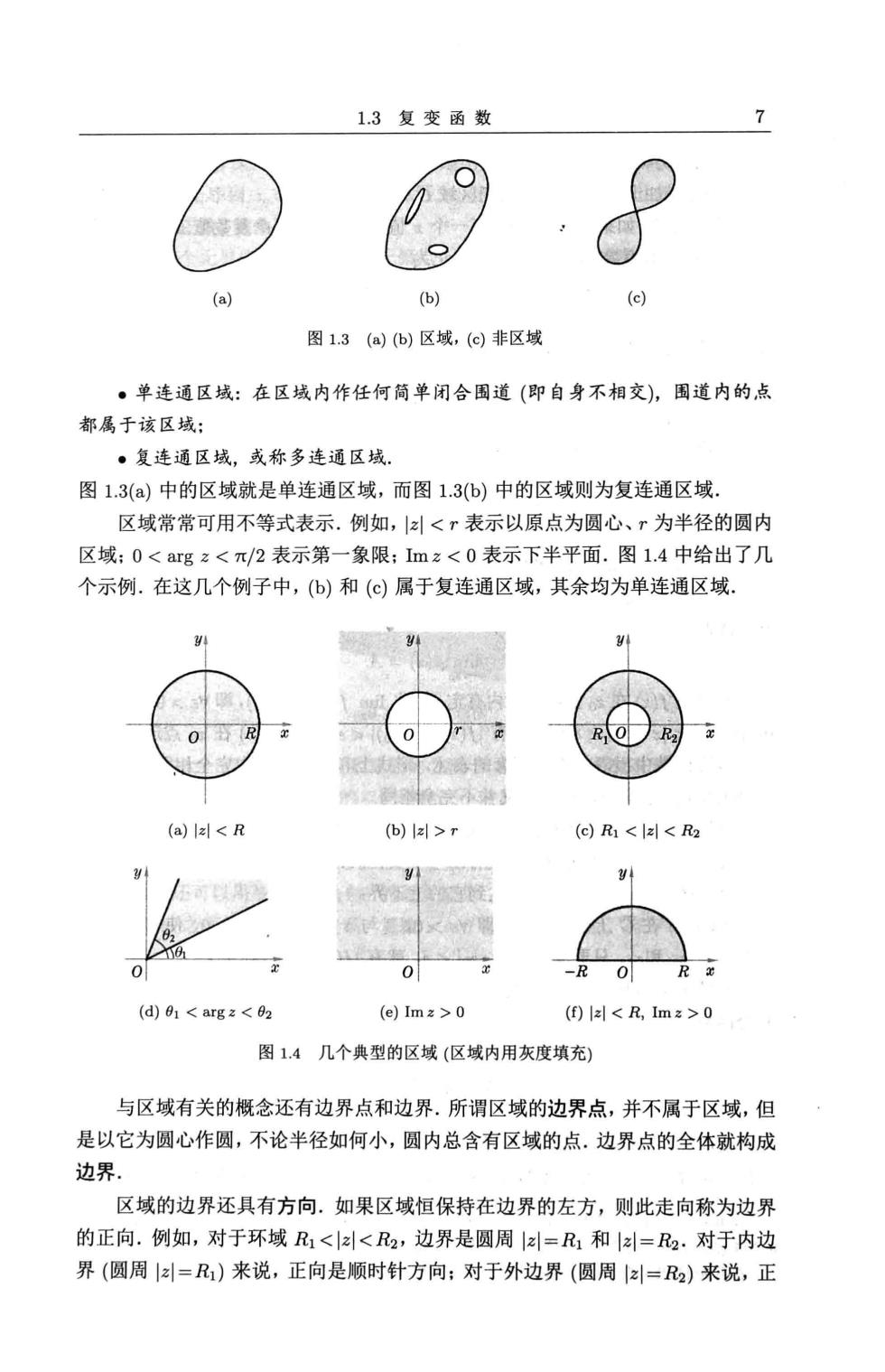
13复变函数 7 O (a) 6 图1.3(a)(b)区域,(c)非区域 。单连通区域:在区域内作任何简单闭合围道(即自身不相交),围道内的点 都属于该区域: 。复连通区域,或称多连通区域. 图1.3(a)中的区域就是单连通区域,而图1.3(b)中的区域则为复连通区域. 区域常常可用不等式表示.例如,z<r表示以原点为圆心、r为半径的圆内 区域:0<argz<π/2表示第一象限:1mz<0表示下半平面.图1.4中给出了几 个示例.在这几个例子中,(b)和(©)属于复连通区域,其余均为单连通区域. (a)<R ()>r ()R<ld<R2 0 0 (d)01 argz<02 (e)Im2>0 (f)<R,Im2 >0 图1.4几个典型的区域(区域内用灰度填充) 与区域有关的概念还有边界点和边界.所谓区域的边界点,并不属于区域,但 是以它为圆心作圆,不论半径如何小,圆内总含有区域的点.边界点的全体就构成 边界. 区域的边界还具有方向.如果区域恒保持在边界的左方,则此走向称为边界 的正向.例如,对于环域R1<<R2,边界是圆周=R1和=2·对于内边 界(圆周=凡)来说,正向是顺时针方向:对于外边界(圆周=2)来说,正

8 第一章复数和复变函数 向是逆时针方向。 区域G加上边界C就构成闭区域G.G=G+C. 设G∈C,如果对于G内的每一个z值,有一个或多个复数值w与之对应, 则称w为:的函数一复变函数,记为 w=f(z). 定义域为G.因为z=x+iy,所以 w=f(z)=u(z,)+iv(,) 一个复变函数只不过是两个二元实变函数的有序组合。 1.4复变函数的极限和连续 设函数f()在0点的空心邻域①内有定义,若存在复数A,e>0,3(e)> 0,使当0<z-20l<6时,恒有f(2)-A<e,则称z→0时f(2)的极限(=A)存 在,且表示为 lim f()=A. 设函数fa)在0点的邻域内有定义,且mf八)=(2o,即e>0,36e)> 0,使当0<z-0l<6时,恒有f(a)-f(2ol<e,则称f(2)在0点连续. 复变函数中极限和连续概念的表述,形式上和实变函数中完全相同.但由于 涉及的数域不同,因此实际含义并不完全相同. 函数在区域G内每一点都连续,称为在G内连续 在闭区域G上连续的函数具有两个重要性质: (1)f(z训在G上有界,并达到它的上下界: (②)f()在G上一致连续,即E>0,3与z无关的6阳)>0,使G上的任 何两个点和2,只要满足名-2<6,就有f(a)-f(22训<. 连续函数的和、差、积、商(在分母不为零的点)仍为连续函数,连续函数的 复合函数也仍为连续函数. 1.5无穷远点 前面1.3节中已经介绍过有界序列必有聚点的结论.对于无界序列{z,给 定任意正数M,不存在正整数N,使当n>N时,l2<M.换句话说,总有无穷 ①所谓0点的空心邻域,指的是以0点为圆心的环域0<2一0<6.相关的概念还有0点的 香邻拔(简称邻域,则是以0点为圆心的圆域:-01<:有时也称作0点及其邻城,以示强调。 在不易引起歧义的情况下,有时也将空心邻域称作邻域

1.6阅读材料:正十七边形的规尺作图原理 9 多个n满足n>M.这时我们就说0是无界序列的(一个)聚点.例如z=1 和z=0就是序列n=1,2,1,4,1,6,1,8,.的两个聚点.0∞也是一个数:其日拾遗补阙 模大于任何正数,辐角不定。 对o∞的理解 如果一个无界序列在有限远处无聚点,那么,∞就是它的唯一的聚点,或称 无界序列收敛于o∞. ∞也对应于复数平面上的一点(称为无穷远点):以任意方式无限地远离原点 即可到达无穷远点.包含有无穷远点的复数平面称为扩充了的复数平面,记作C. 为了更直观地表现无穷远点,还可以引进复数球面.过复数平面C上的原点 (0,0)作直径为1的球面,使与C相切,切点称为南极.过南极的直径的另一端称 为北极N.此球面就称为复数球面,如图1.5. 图1.5复数球面 对于C,上一点z,将它和复数球面的北极N相连,此连线和球面必有一交点, 因此,复数球面上的点和C上的点也存在一一对应关系.于是就可以用复数球面 上的交点来表示复数z,例如南极对应于复数0,赤道对应于C上的单位圆周.令 C上的点无限远离原点,就得到∞点在复数球面上的对应点一北极N.对于 无穷远点,还可以用变换(或映射)的语言定义.例如变换w=1/z就建立了复数 z和复数w之间的一一对应关系.复数z=0对应于w=0,而:=0对应于 w=0. 1.6阅读材料:正十七边形的规尺作图原理 本节用复数方法讨论一个几何学问题:正十七边形的圆规直尺作图问题.设 有正十七边形,内接于单位圆.下面就来求出a=2si血(π/17)的代数表达式. 设z=e2m17,由于20,2,2子,.,216都是方程17-1=0的根,0+z+22+ .+z16=0,即z2+2+23+.+216=-1.令 8=2+29+29”+.+291 =z2+z9+z18+215+z16+28+z4+2