
1.写出下列复数的实部,虚部,模和幅角: (1)1+W3:(2)1-cosa+isina,0≤a<2π:(3)emx,x为实数:(4)e: 0d:6:):0哥o产:0em,p是实 的实函数。 we=1.m=5,Aa=c+m-2.Ag=02-号+2a (2)Re=1-cosa,Im=sina,Am=(1-cosa)'+sina=2-2cosa=2sin tan(Arg)-singr2sin cos =o所以Ag-+2r 2sin号 2 (3)Am=1,Arg=sinx+2kz,Re=cos(sinx),Im=sin(sinx): (4)z=x+y,e=e“,Am=ey,Arg=x+2kπ,Re=e'cosx,m=e'sinx (5)Am=e,Arg=y+2kπ,Re=e'cosy,Im=e'siny: o-e-e学,a=2外Aa=1.Ng2n+2, Re-ow im-sin )i=5em泸-5ef传-,m=0.wAm-5,Ag-g+m+2a Re2cosc Im-(sin m周-于学.子 Re=” (9)Am=e,Arg=l+2kπ,Re=ecos1,Im=esinl (10)Am=1,Arg=(x)+2kz,Re=cos[o(x)].Im=sin[o(x)]:
1.写出下列复数的实部,虚部,模和幅角: (1)1 3 + i ;(2)1 cos sin − + α i α ,0 2 ≤α < π ;(3) i x sin e , x 为实数;(4) iz e ; (5) z e ;(6) 4 −1;(7) 1+ i ;(8) 1 1 i i + − ;(9) 1 i e + ;(10) i x( ) e ϕ ,ϕ ( ) x 是实变数 x 的实函数。 (1)Re 1 = ,Im 3 = , 2 2 Am Re Im 2 = + = , Im Arg arctan 2 2 Re 3 k k π π π ⎛ ⎞ ⎜ ⎟ + =+ ⎝ ⎠ = ; (2)Re 1 cos = − α ,Im sin = α , ( )2 2 Am 1 cos sin 2 2cos 2sin 2 = α − + =− = αα α , ( ) 2 2sin cos sin 2 2 tan Arg cot 1 cos 2 2sin 2 α α α α α α == = − ,所以 Arg 2 2 = k π α π − + ; (3)Am 1 = , Arg sin 2 =xk + π , Re cos sin = ( x) ,Im sin sin = ( x) ; (4)z x iy = + , iz y ix e e− + = ,Am y e− = ,Arg 2 =x k + π ,Re cos y e x − = ,Im sin y e x − = ; (5)Am x = e , Arg 2 =y k + π , Re cos x = e y , Im sin x = e y ; (6) ( ) 1 2 1 4 2 4 4 1 n i i n e e π π π + + −= = ⎡ ⎤ ⎣ ⎦ ,( n = 0,1,2,3),Am 1 = , 2 1 Arg 2 4 n = k π π + + , 2 1 Re cos 4 n = π ⎛ ⎞ + ⎜ ⎟ ⎝ ⎠, 2 1 Im sin 4 n = π ⎛ ⎞ + ⎜ ⎟ ⎝ ⎠; (7) 2 2 4 4 4 8 12 2 i n in ie e π π π π ⎛ ⎞ ⎛⎞ ⎜ ⎟ ⎜⎟ + + ⎝ ⎠ ⎝⎠ += = ,( n = 0,1), 4 Am 2 = ,Arg 2 8 =n k π + + π π , ( ) 4 4 Re 2 cos 1 2 cos 8 8 n n π π π ⎛ ⎞ = + =− ⎜ ⎟ ⎝ ⎠ , ( ) 4 Im 1 2 sin 8 n π = − ; (8) ( ) 1 4 2 2 2 2 2 4 4 1 2 1 2 i n n i i n i i e e e i e π π π π π π π + + ⎛ ⎞ ⎜ ⎟ + ⎝ ⎠ − + ⎡ ⎤ = == ⎢ ⎥ − ⎣ ⎦ ,( n = 0,1),Am 1 = ,Arg 2 4 =n k π + + π π , ( ) 1 Re 2 n − = , ( ) 1 Im 2 n − = ; (9)Am = e , Arg 1 2 = + kπ , Re cos1 = e ,Im sin1 = e ; (10)Am 1 = , Arg 2 =x k ϕ ( ) + π , Re cos = ⎡ϕ ( x)⎤ ⎣ ⎦ , Im sin = ⎡ϕ ( x)⎤ ⎣ ⎦ ;

2.把下列关系用几何图形表示出来: )<2,H-=2,2:(2)Re>,1<m<2:(3)ag-)=0, ag+)-了,a照e+1-小-7:(4)0<g0-水牙,0<ag+小<4 子<g(el-2<胥:6a<a吗:<月与7<Re:<6的公共区城a,A.7,6 均为常数:(6)上-<1,1<-<反:(7)-d=上-,a,b为常数:(8) -d+-l=c,其中a,b,c,为常数,且c>a-b:(9)+Rez<l:(10) 0<号 (1) (3)arg(1-)=arg(1-x-y)=0台1-x>0且y=0,即x<1,y=0 ag(+)=arg1+x+)=台1+x>0且y=51+x: rg(e+1-)=arg[x+1+i(y-l)]=5x+1=0且y-1>0
2.把下列关系用几何图形表示出来: (1) z < 2 , z = 2 , z > 2 ;(2) 1 Re 2 z > ,1 Im 2 < z < ;(3) arg 1 0 ( ) − = z , arg 1( ) 3 z π + = , arg 1 ( ) 2 z i π +− = ;(4 ) 0 arg 1( ) 4 z π < − < , 0 arg 1( ) 4 z π < + < , arg 1 2 ( ) 4 3 z i π π < −− < ;(5)α < < arg z β 与γ < Re z < δ 的公共区域,α ,β ,γ ,δ 均为常数;(6) z i − <1,1 2 < −< z i ;(7) za zb − = − , a , b 为常数;(8) za zb c −+−= ,其中 a , b , c ,为常数,且 c ab > − ;(9) z z + Re 1 < ;(10) 0 arg 4 z i z i ⎛ ⎞ − π < < ⎜ ⎟ ⎝ ⎠ + 。 (1) (2) (3)arg 1 arg 1 0 () ( ) − = −− = z x iy ⇔ 1 0 − x > 且 y = 0,即 x <1, y = 0; arg 1 arg 1 1 0 () ( ) 3 z x iy x π + = + + = ⇔+ > 且 y x = 3 1( + ) ; arg 1 arg 1 1 1 0 ( ) () 2 z i x iy x π +− = ++ − = ⇔ += ⎡ ⎤ ⎣ ⎦ 且 y −1 0 >
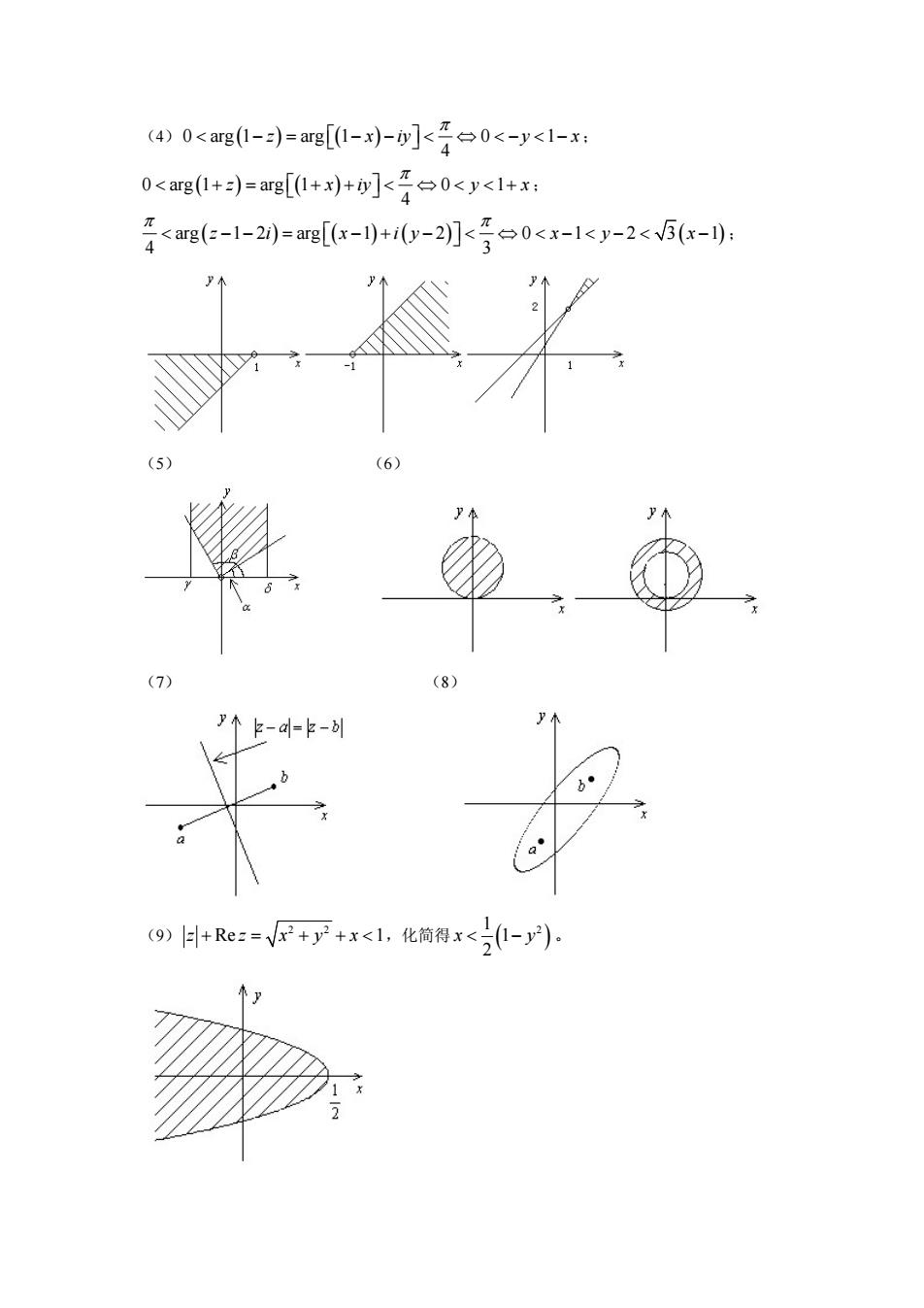
(4)0<arg-)=arg[-x-]<年台0<-y<l-x: 0<agl+)=arg[0+x+]<平台0<y<1+x: 牙<a8e-1-2)=ag[0x-+i0y-2]小<号台0<x-1<y-2<V5(x-): 5 (9)+Re:=V++x<1,化简得x<(1-y2)
(4)0 arg 1 arg 1 0 1 () () 4 z x iy y x π < − = − − < ⇔ <− < − ⎡ ⎤ ⎣ ⎦ ; 0 arg 1 arg 1 0 1 () () 4 z x iy y x π < + = + + < ⇔ < <+ ⎡ ⎤ ⎣ ⎦ ; arg 1 2 arg 1 2 0 1 2 3 1 ( ) ( )( ) ( ) 4 3 z i x iy x y x π π < −− = − + − < ⇔ < −< − < − ⎡ ⎤ ⎣ ⎦ ; (5) (6) (7) (8) (9) 2 2 z z xyx + = + +< Re 1,化简得 ( ) 1 2 1 2 x < − y

w计周所0 0<-2x<x2+y2-1,即x<0且(x+1)2+y2>2。 3已陶-复数,面出,-,三,是上并指出它们之的儿何关系 把:写成pe”,则正=pe0+n,即把:逆时针旋转90度。-z=peo),即把:逆时到 装转0度。三=心,即:关于实箱的对称点。},即:关于华位圆的对称点· 41流证到医部1,a,6为任室复数 医-传阁谱
(10) ( ) ( ) ( ) 2 2 2 2 1 1 2 1 1 z i x y ix x iy z i x iy x y − + −− + − = = + ++ + + ,所以0 arg 4 z i z i ⎛ ⎞ − π < ⎜ ⎟ < ⎝ ⎠ + ⇔ 2 2 02 1 <− < + − xx y ,即 x < 0 且( )2 2 x y +1 2 + > 。 3.已知一复数 z ,画出iz , −z , z , 1 z , 1 z ,并指出它们之间的几何关系。 把 z 写成 i e ϕ ρ ,则 i( 2) iz e ϕ π ρ + = ,即把 z 逆时针旋转 90 度。 i( ) z e ϕ π ρ + − = ,即把 z 逆时针 旋转 180 度。 i z e ϕ ρ − = ,即 z 关于实轴的对称点。 1 1 i e z ϕ ρ = ,即 z 关于单位圆的对称点。 1 1 i e z ϕ ρ − = ,即 z 关于单位圆的对称点。 4.若 z =1,试证明 1 az b bz a + = + , a ,b 为任意复数。 ( )( ) ( )( ) 2 2 2 2 2 1 az b az b az b a abz abz b bz a bz a bz a b abz abz a + + + +++ == = + + + +++ ,所以 1 az b bz a + = +

5.证明下列各式: (1 -1s-1+arg: o补-产-即子 D先证5 记:=p, -1"2-2cs-2sin 2slol-larg=. -H*-s-后g (2) 国。与在得一圆周上、《=野等B=子,由于同所对周周角是 风6角价-卡所-,事ag浮-子 6.用复数:表示曲线上的变点。(I)写出经过点α且与复数b所代表的矢量平行的直线方 程:(2)写出以d和-d为焦点,长轴长2a的椭圆方程(a>d)。 (1)矢量:-a与矢量b平行,所以:-a=kb,k为实数: (2)由椭圆定义得-d+上+d=2a. 7.用复数运算法则推出:(1)平面直角坐标平移公式:(2)平面直角坐标旋转公式
5.证明下列各式: (1) z z zz −≤ −+ 1 1 arg ; (2)若 123 zz z = = ,则 3 2 2 31 1 1 arg arg 2 z z z zz z − = − 。 (1)先证 1 arg z z z − ≤ 。 记 i z e ϕ = ρ , 1 1 2 2cos 2 sin arg 2 z i e z z ϕ ϕ −= −= − = ≤ = ϕ ϕ 。 1 1 1 1 1 1 arg z z zz z zz z z z z z z z −= − + −≤ − + −= −+ −≤ −+ 。 (2) 如图, 1z , 2 z , 3 z 在同一圆周上, 3 2 3 1 arg z z z z α − = − , 2 1 arg z z β = 。由于同弧所对圆周角是 圆心角的一半,所以 1 2 α = β ,即 3 2 2 31 1 1 arg arg 2 z z z zz z − = − 。 6.用复数 z 表示曲线上的变点。(1)写出经过点 a 且与复数b 所代表的矢量平行的直线方 程;(2)写出以 d 和 −d 为焦点,长轴长 2a 的椭圆方程( a d > )。 (1)矢量 z a − 与矢量b 平行,所以 z a kb − = , k 为实数; (2)由椭圆定义得 zd zd a −++ = 2 。 7.用复数运算法则推出:(1)平面直角坐标平移公式;(2)平面直角坐标旋转公式