
9.2弯曲正应力的强度条件及其应用 1、变形几何关系 综合考虑 2、物理关系 3、静力学关系
综合考虑 1、变形几何关系 2、物理关系 3、静力学关系 9.2 弯曲正应力的强度条件及其应用

(p+y)a服-pd m 、y n p昶 p m n 合形见回关系 M M 中性轴 静矩 n R=小12片胸理关系 m 0 dA M,=jFom=」,34=0 惯性积 m =M dx 曲率半径P 曲率 惯性矩 y 曲率 3、静力学关系 p 抗弯刚度
dx m m n n o z y ρ dθ m m n n F F y ( ) yd d d ρ θ ρθ ε ρ θ + − = y ρ = σ ε = E y E ρ = M M 中性轴 y z dA σ ∫A FN = σdA ∫A Miy = zσdA ∫A Miz = yσdA A E ydA ρ = ∫ = 0 A E zydA ρ = ∫ = 0 2 A E y dA ρ = ∫ EI z ρ = 1 z M ρ EI = 1、变形几何关系 2、物理关系 = M 3、静力学关系 惯性矩 抗弯刚度 曲率半径 ρ 曲率 1 ρ 静矩 惯性积 曲率 m n m n dx d = ρ θ z My I σ =
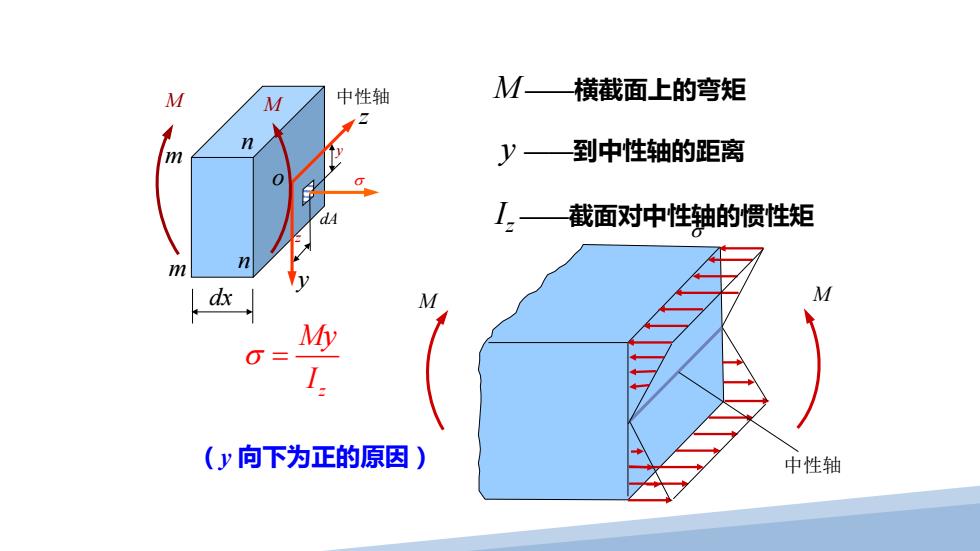
M M 中性轴 M一横截面上的弯矩 n y 到中性轴的距离 截面对中性轴的惯性矩 m n dx M M My (y向下为正的原因) 中性轴
M ——横截面上的弯矩 y ——到中性轴的距离 Iz ——截面对中性轴的惯性矩 M σ 中性轴 M (y 向下为正的原因) dx m m n n o z y M M 中性轴 y z dA σ z My I σ =

Tianiin yai P a a a anmn Inversity Mvecha e5ya©a0Cs Tianiin Univers海w Tan通 aniin University Mechanics Fianiin Univers lecnanics wGa0图 Tianiin Universiy aity Me

My 横截面上正应力的画法:σ= Omin M 性 公式适用范围: ①线弹性范围一正应力小于比例极限σ,; ②精确适用于纯弯曲梁; ③对于横力弯曲的细长梁(跨度与截面高度比L>5),上述公式的误差不 天,但公式中的应为所研究截面上的弯矩,即为截面位置的函数。 M(x)y 1 M(x) O= (x) EI
横截面上正应力的画法: σmin M σmax σmin M σmax ①线弹性范围—正应力小于比例极限σp; ②精确适用于纯弯曲梁; ③对于横力弯曲的细长梁(跨度与截面高度比L/h>5),上述公式的误差不 大,但公式中的M应为所研究截面上的弯矩,即为截面位置的函数。 公式适用范围: () 1 () ( ) z z Mxy M x I x EI σ ρ = = M σ 中性轴 M z My I σ =