
一、广义胡克定律 1、单拉压的应力-应变关系 -E 8 8'=-l8 2、纯剪的应力-应变关系 Y=- ,0(i=x,y,z) Y=Y0
1、单拉压的应力--应变关系 ε µε σ ε ′ = − = E 2、纯剪的应力--应变关系 G τ γ = 0 (i x,y,z) ε i≈ = γ yz =γ zx ≈0 σ x y z τx y 一、 广义胡克定律

3、复杂状态下的应力--应变关系 共有六个独立得分量 小变形情况下,认为o引起6,x引起y Ox 2 依叠加原理,得: 61 X
3、复杂状态下的应力 --- 应变关系 依叠加原理,得: x y z σz σy τxy σx 小变形情况下,认为σ引起ε, τ 引起γ x y z τxy x y z σz σy σx = + 共有六个独立得分量
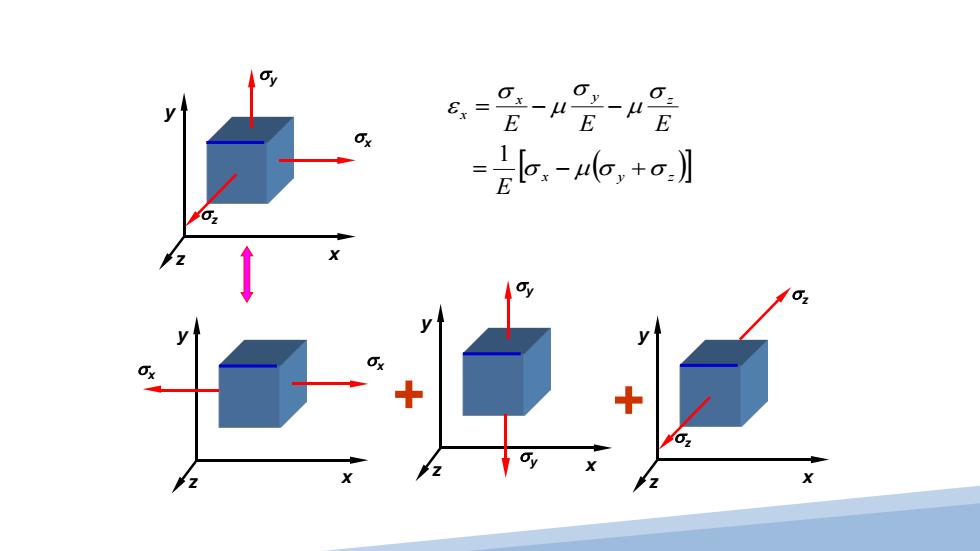
8x= E E 2k.-6,+a】 y
[ ( )] x y z x y z x EE E E σ µ σ σ σ µ σ µ σ ε = − + = − − 1 x y z σz σx σy + + x y z σ σx x x y z σyσy x y z σz σz
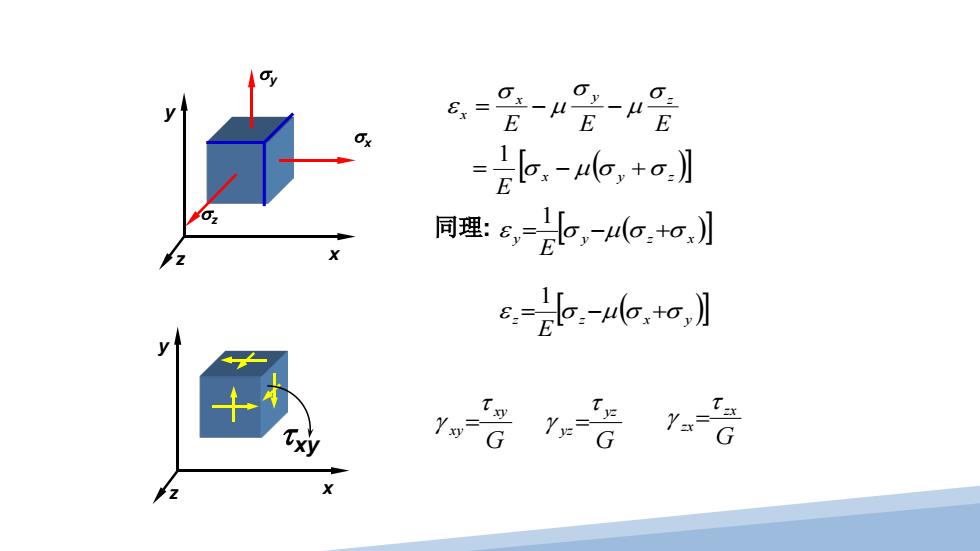
8x= E =2-h6,+o】 同理:£,,6o小 e--o,o,月 ro= G G
[ ( )] x y z x y z x E E E E σ µ σ σ σ µ σ µ σ ε = − + = − − 1 x y z τxy x y z σz σx σy [ ( )] y y z x E ε = σ −µ σ +σ 1 [ ( )] z z x y E ε = σ −µ σ +σ 1 G xy xy τ γ = G yz yz τ γ = G zx zx τ γ = 同理:
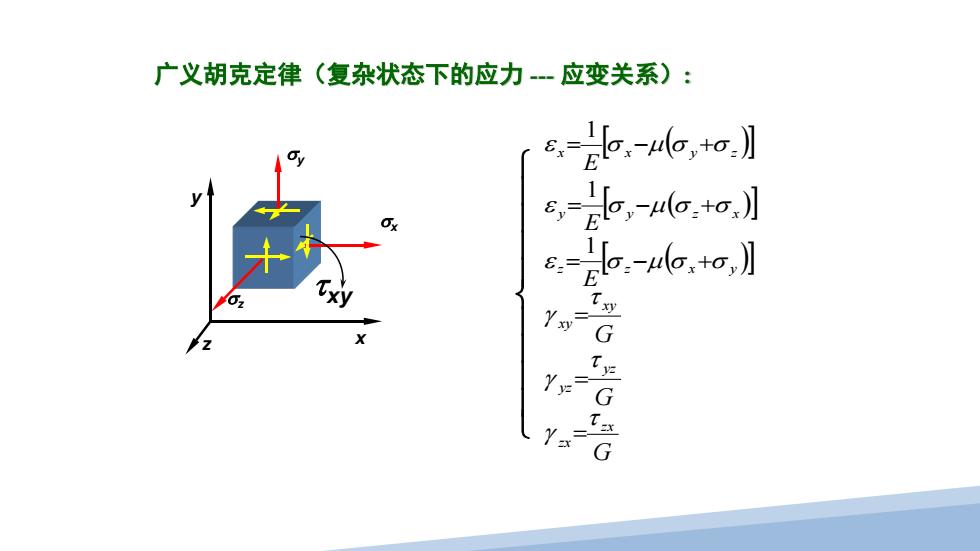
广义胡克定律(复杂状态下的应力--应变关系): 8,l,a】 -g,hao】 c-o+o,】 G Y= G Y G
广义胡克定律(复杂状态下的应力 --- 应变关系): [ ( )] y y z x E ε = σ −µ σ +σ 1 [ ( )] z z x y E ε = σ −µ σ +σ 1 G xy xy τ γ = G yz yz τ γ = G zx zx τ γ = [ ( )] x x y z E ε = σ −µ σ +σ 1 x y z σz σy τxy σx