
目录 CONTENTS 人 稳定安全系数 2 稳定条件与强度条件比较 3 例题 4 提高压杆稳定性措施
1 2 3 稳定安全系数 稳定条件与强度条件比较 例题 目录 CONTENTS 4 提高压杆稳定性措施

1.稳定安全系数 理想压杆:1)材料均匀;2)轴线笔直;3)载荷无偏心 实际压杆:1)材料缺陷;2)轴线初弯;3)载荷偏心 稳定条件:安全系数法 稳定工作安全系数:n= 许用的稳定安全系数” P 稳定条件 n= 满足稳定性要求
1. 稳定安全系数 理想压杆:1)材料均匀; 2)轴线笔直; 3) 载荷无偏心 实际压杆: 1)材料缺陷 ;2)轴线初弯;3)载荷偏心 稳定条件:安全系数法 稳定工作安全系数: 许用的稳定安全系数 稳定条件 满足稳定性要求 P P n cr = st n P P n cr = st ≥ n
2.稳定条件与强度条件比较 1)稳定条件 n之nst 2)强度条件 0之0max 稳定安全系数与强度安全系数的取值: 强度安系数取值1.2~2.5,有时可达3.5: ⊕ 稳定安全全系数取值2~5,有时可达8~10。 3)计算横截面、惯性矩时 稳定:不考虑局部削弱面积 强度:必须考虑
2. 稳定条件与强度条件比较 1)稳定条件 2)强度条件 3)计算横截面、惯性矩时 稳定:不考虑局部削弱面积 强度:必须考虑 st n ≥ n σ ≥ σ max 稳定安全系数与强度安全系数的取值: 强度安系数取值 1.2 ~ 2.5,有时可达 3.5; 稳定安全全系数取值 2 ~ 5,有时可达 8 ~10

1500 500 D 3.例题 30° 已知托架D处承受荷载F=10kN。AB杆外径D=50mm, A 内径d=40mm,材料Q235钢,E=200 GPa。元n=100·n=3。 1500 500 试校核AB杆的稳定性。 30 解:计算AB杆的轴力 CD梁 ∑Mc=0 F.2000=F×·sin30°.1500 得Fx=26.6kN AB杆元=叫 4=1 (两端铰支)》 i l=_ 1.5 =1.732m AB杆截面 c0s30°
CD梁 0 ∑ MC = AB 杆 i µl λ = µ = 1 1.5 1.732 m cos30 l = = 已知托架 D 处承受荷载 F = 10 kN。AB杆外径D = 50 mm, 内径 d = 40 mm,材料Q235钢,E = 200 GPa。 λ p =100 , nst = 3 。 试校核 AB 杆的稳定性。 计算 AB 杆的轴力 得 FN = 26.6 kN 2000 sin 30 1500 F FN ⋅ =⋅ ⋅ (两端铰支) 解: 3. 例题
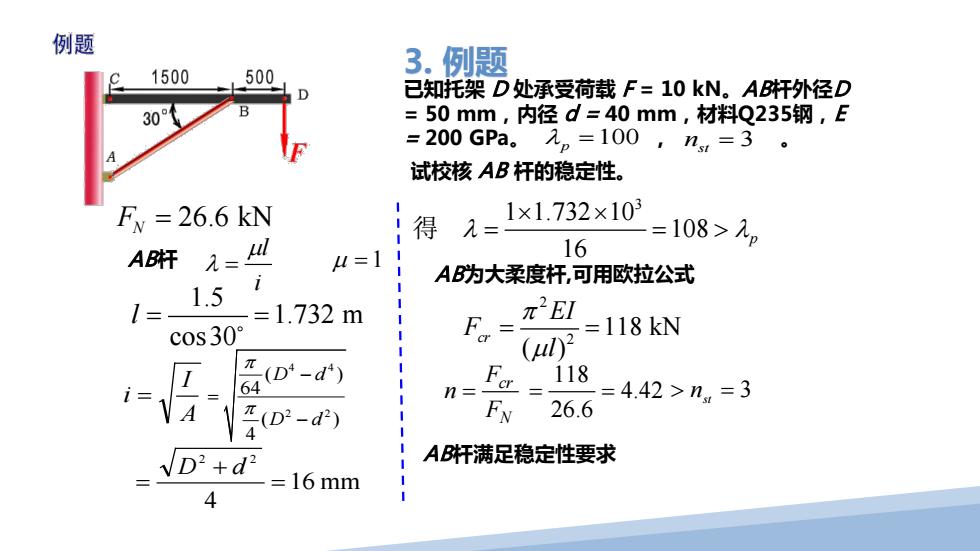
例题 1500 500 3.例题 D 已知托架D处承受荷载F=10kN。AB杆外径D 30 =50mm,内径d=40mm,材料Q235钢,E =200GPa。入p=100,nm=3· 试校核AB杆的稳定性。 Fy =26.6 kN 得 1= 1×1.732×103 =108>2 AB杆 A=ul 4=11 16 i AB为大柔度杆,可用欧拉公式 /= 1.5 =1.732m c0s30° F= π2E1 =118kN cr π (l2 1 (D4-d4) F 118 64 n= =4.42>nm=3 π(D2-d) FN 26.6 D'+d" AB杆满足稳定性要求 =16mm 4
FN = 26.6 kN AB杆 i µl λ = µ = 1 1.5 1.732 m cos30 l = = A I i = 3 1 1.732 10 108 16 λ λ p × × 得 = = > AB为大柔度杆,可用欧拉公式 2 2 118 kN ( ) cr EI F l π µ = = N cr F F n = 4.42 26.6 118 = = AB杆满足稳定性要求 > = 3 st n 4 4 2 2 ( ) 64 ( ) 4 D d D d π π − = − 16 mm 4 2 2 = + = D d 已知托架 D 处承受荷载 F = 10 kN。AB杆外径D = 50 mm,内径 d = 40 mm,材料Q235钢,E = 200 GPa。 λ p =100 , nst = 3 。 试校核 AB 杆的稳定性。 3. 例题