二向应力状态的普遍形式如图所示,单元体上有C,w和o,Tx
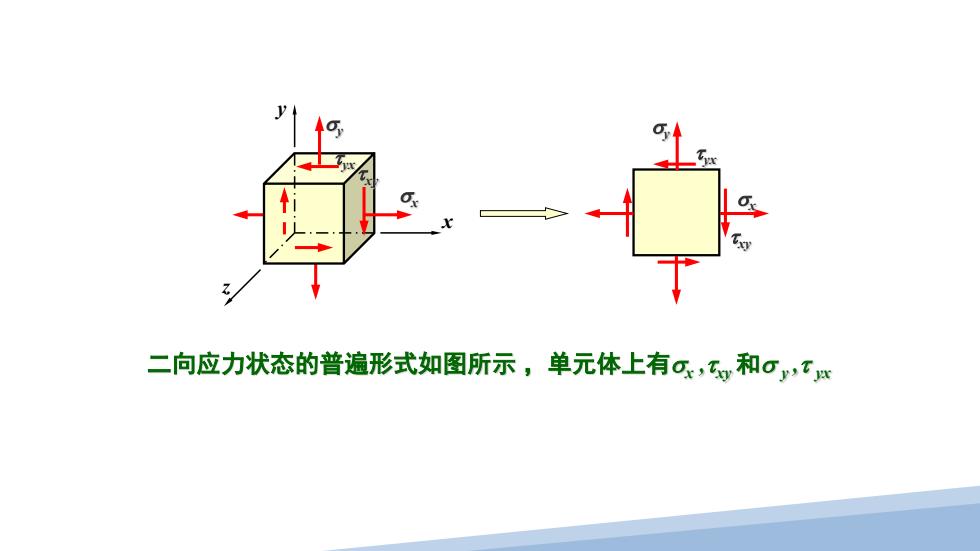
二向应力状态的普遍形式如图所示 ,单元体上有σx ,τ xy和σ y ,τ yx x σx y z σy τ xy τ yx σx σy τ xy τ yx
一、斜截面上的应力 1.截面法 假想地沿斜截面e-f将单元体截开, 留下左边部分的单体元egf作为研究对橡 n
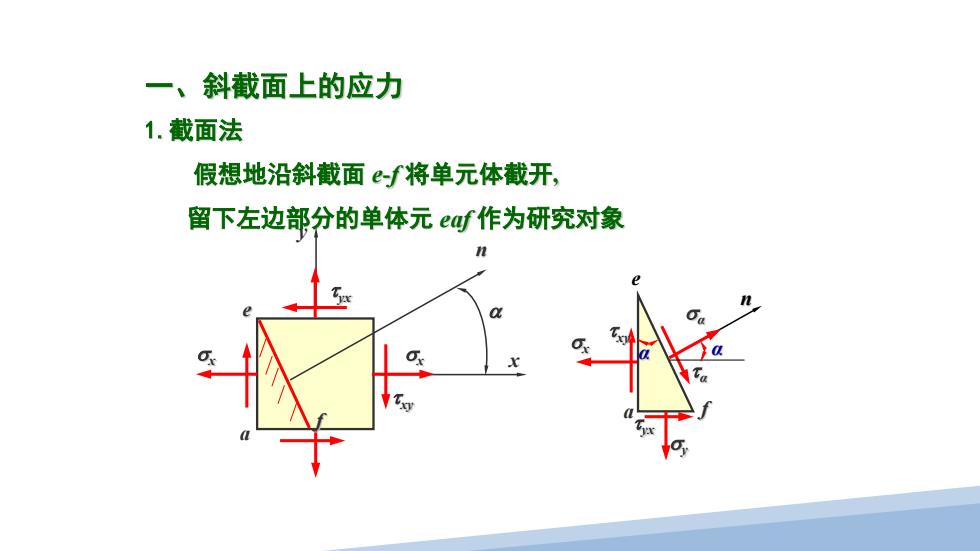
一、斜截面上的应力 1.截面法 假想地沿斜截面 e-f 将单元体截开, 留下左边部分的单体元 eaf 作为研究对象 x y a σx σx τ yx τ xy e f α n e a f σx τ xy τ yx σy σα τα α n α
-Xy L xy

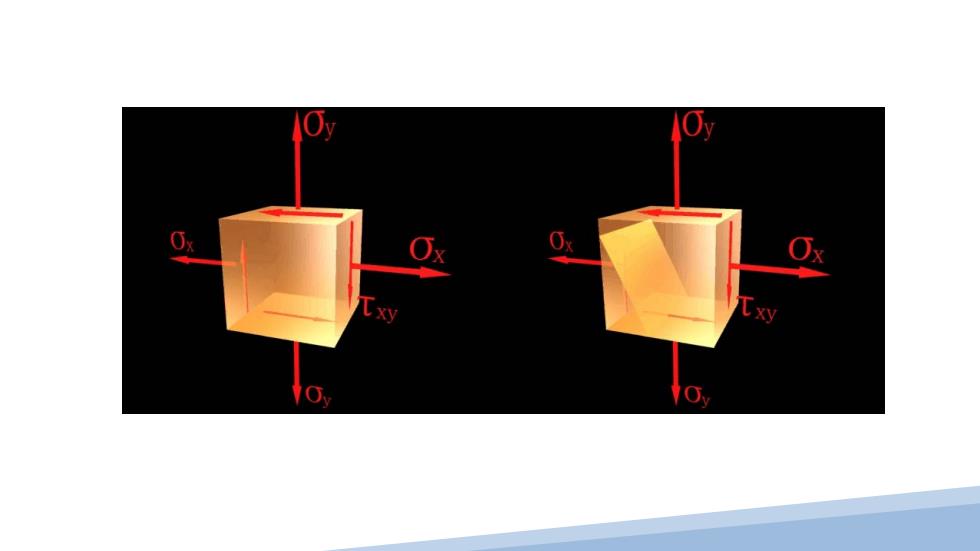
n 2.符号的确定 (1)由轴转到外法线n, X 逆时针转向时a为正 (2)正应力仍规定 拉应力o为正 o x (3)切应力对单元体内任一点取矩, 顺时针转为正 人 ⊕
(1)由x轴转到外法线n, 逆时针转向时α为正 (2)正应力仍规定 拉应力σ为正 (3)切应力对单元体内任一点取矩, 顺时针转τ为正 2.符号的确定 n τ x α α σ y σ x σ x α τ y τ x τ

dAsina 3.任意斜截面上的应力 设斜截面的面积为dA,-e的面积为dAcosa,-f的面积为 dAsina 对研究对象列n和t方向的平衡方程得 ∑Fn=0o.dA+(亿,dAcosa)sina-(o,dAcosa)cosa+ (dAsin a)cosa-(o,dAsina)sina =0
设斜截面的面积为dA , a-e的面积为dAcosα, a-f 的面积为 dAsinα e a f σx τ xy τ yx σy σα τα α n α e a f α dA dAsinα dAcosα 3.任意斜截面上的应力 对研究对象列 n和 t 方向的平衡方程得 ( d sin )cos ( d sin )sin 0 0 d ( d cos )sin ( d cos )cos − = ∑ = + − + τ α α σ α α σ α τ α α σ α α A A F A A A yx y n xy x t