
一、应力圆 将斜截面应力计算公式改写为 s+_x-Ox cos2a-Exy simn 2a 2 2 0x- Ta y 2 sin 2a+Tx cos 2a 把上面两式等号两边平方,然后相加便可消去,得 a.-y+=82y+
sin cos cos sin α τ α σ σ τ α τ α σ σ σ σ σ α α 2 2 2 2 2 2 2 xy x y xy x y x y + − = − − = + − 一、应力圆 将斜截面应力计算公式改写为 把上面两式等号两边平方,然后相加便可消去α,得 2 2 2 2 2 2 xy x y x y τ σ σ τ σ σ σ α α + − + = + ( − ) ( )

+0+=:,02+ 2 2 因为g,g,,皆为已知量,所以上式是一个以o,为变 量的圆周方程。当斜截面随方位角a变化时,其上的应力oa,Ta 在σ-x直角坐标系内的轨迹是一个圆。 1.圆心的坐标 0+0,0) 2 2.圆的半径 R=2+ 此圆习惯上称为应力圆,或称为莫尔圆
2 2 2 2 2 2 xy x y x y τ σ σ τ σ σ σ α α + − + = + ( − ) ( ) 因为σx , σy , τ xy皆为已知量,所以上式是一个以σα, τα为变 量的圆周方程。当斜截面随方位角 α 变化时,其上的应力σα , τα 在σ -τ 直角坐标系内的轨迹是一个圆。 1.圆心的坐标 ( ,0) 2 x y C σ + σ 2.圆的半径 2 2 2 xy x y R τ σ σ + − = ( ) 此圆习惯上称为 应力圆,或称为莫尔圆
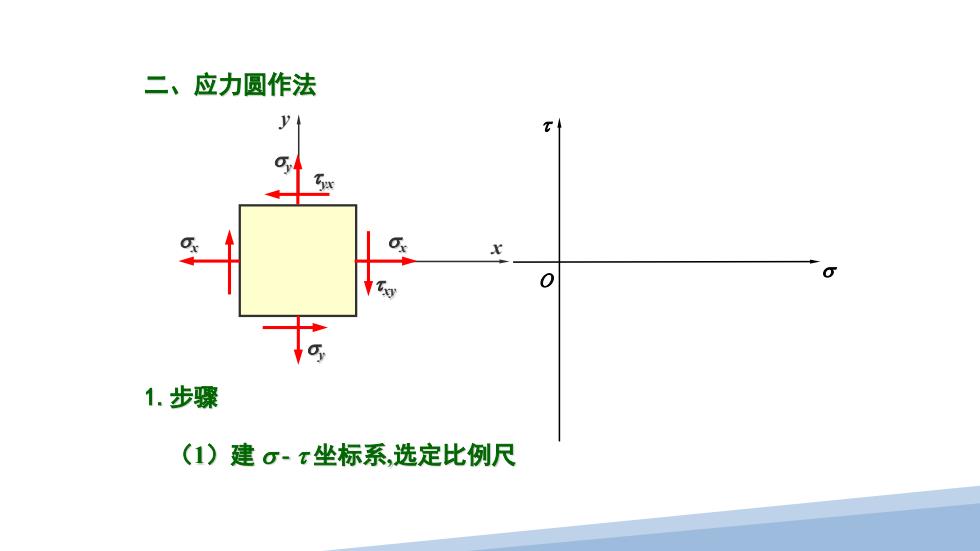
二、应力圆作法 y T Oy 0 0 1.步骤 (1)建σ~x坐标系,选定比例尺
(1)建 σ - τ 坐标系,选定比例尺 O τ σ 二、应力圆作法 1.步骤 x y σx σx τ yx τ xy σy σy
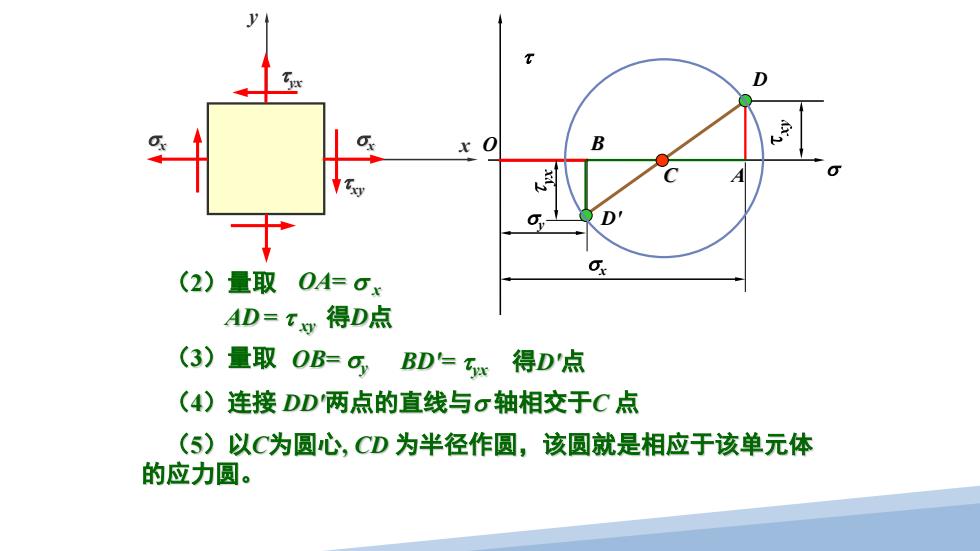
D B 人对 D' (2)量取 OA=Ox C AD=T得D点 (3)量取OB=CBD=Tx 得D点 (4)连接DD两点的直线与σ轴相交于C点 (5)以C为圆心,CD为半径作圆,该圆就是相应于该单元体 的应力圆
D O τ σ (2)量取 OA= σ x AD = τ xy 得D点 x y σx σx τ yx τ xy σx A OB= σy (3)量取 BD′= τ yx 得D′点 σy B D′ (4)连接 DD′两点的直线与σ 轴相交于C 点 (5)以C为圆心, CD 为半径作圆,该圆就是相应于该单元体 的应力圆。 C

三、应力圆的应用 1.求单元体上任一截面上的应力 从应力圆的半径CD按方位角a的转向转动2a得到半径CE, 圆周上E点的坐标就依次为斜截面上的正应力o,和切应力x。 E D 2a B 人
三、应力圆的应用 1.求单元体上任一截面上的应力 从应力圆的半径 CD 按方位角α的转向转动2α得到半径CE, 圆周上 E 点的坐标就依次为斜截面上的正应力σα和切应力τα。 D O τ σ σx A σy B D′ C E 2α x y a σx σx τ yx τ xy e f α n