
10.2梁的挠曲线近似微分方程及其积分 推导纯弯曲正应力时,得到: 1 M EI 上式中,惯性矩I省略了下标z 忽略剪力对变形的影响,此时M和二都是x的函数 p M(x) (x) EI
推导纯弯曲正应力时,得到: 1 M ρ EI = 1 () ( ) M x ρ x EI = ρ 忽略剪力对变形的影响,此时 M 和 都是 x 的函数 1 ρ 上式中,惯性矩 I 省略了下标 z 10.2 梁的挠曲线近似微分方程及其积分

由几何、数学知识推导可得: d2w dx2 挠曲线的微分方程: 73/2 d2w dx2 M 联立弯矩与曲率半径关系式 3/2 dw El 1M P El 小量 M 挠曲线的近似微分方程: d2w 或 Elw"M El
由几何、数学知识推导可得: 2 2 3 2 2 d 1 d d 1( ) d w x w x ρ = + 联立弯矩与曲率半径关系式 1 M ρ EI = 挠曲线的微分方程: 2 2 3 2 2 d d d 1( ) d w x M w EI x = + 小量 2 2 d d w M x EI 挠曲线的近似微分方程: = 或 EIw M ′′ =

挠曲线的近似微分方程为: d2w M d2w .=M dx2 EI dx 积分一次得转角方程: EI0=EI -jx+c 再积分一次得挠度方程: Ew=J∬(Mdx)dr+Cx+D C、D为积分常数,待定
挠曲线的近似微分方程为: 积分一次得转角方程: 再积分一次得挠度方程: 2 2 d d w M x EI = 2 2 d d w EI M x = d d d w EI EI M x C x θ = = + ∫ EIw M x x Cx D = ++ ( d )d ∫∫ C D 、 为积分常数,待定
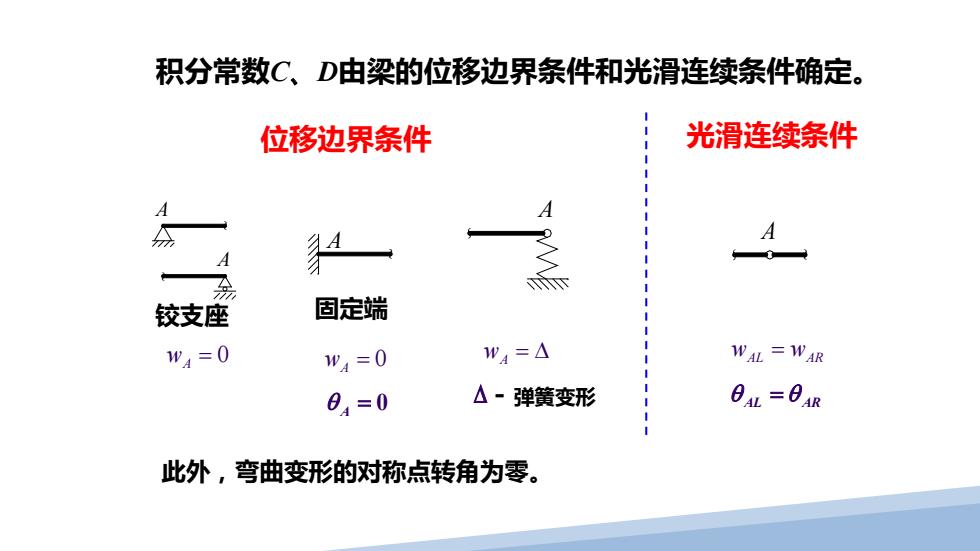
积分常数C、D由梁的位移边界条件和光滑连续条件确定。 位移边界条件 光滑连续条件 A A 分 A 铰支座 固定端 w4=0 w4=0 W4=△ WAL =WAR 04=0 △·弹簧变形 日AL=84R 此外,弯曲变形的对称点转角为零
积分常数C、D由梁的位移边界条件和光滑连续条件确定。 A A ~ ~ A ~ A ~ A 0 wA = 0 wA = = 0 θ A wA = ∆ 位移边界条件 光滑连续条件 w w AL AR = ∆-弹簧变形 θ AL = θ AR 铰支座 固定端 此外,弯曲变形的对称点转角为零

例1 求梁的转角方程和挠度方程,并求截面B处的转角和挠度,梁的EI已知。 解1)为悬臂梁,写出任意处x截面的弯矩方程 M(x)=-F(1-x)=Fx-FI 2)列挠曲线近似微分方程并积分 dw =M(x)=Fx-Fl =E16=F2-Fk+C dw 积分一次 dx 再积分一次 EhW=1Fx-1F+Cx+D 6
例1 求梁的转角方程和挠度方程,并求截面 B 处的转角和挠度,梁的 EI 已知。 解 1)为悬臂梁,写出任意处 x 截面的弯矩方程 M x F l x Fx Fl () ( ) =− − = − 2)列挠曲线近似微分方程并积分 2 2 d ( ) d w EI M x Fx Fl x = = − d 1 2 d 2 w EI EI Fx Flx C x = = −+ θ 1 1 3 2 6 2 EIw Fx Flx Cx D = − ++ 积分一次 再积分一次 θ B A B x w x l F wB