
一、弯矩、剪力与分布荷载集度间的微分关系 二、gx)、F(x)图、M(X)图三者间的关系 三、分布荷载集度、剪力和弯矩之间的积分关系
一、弯矩、剪力与分布荷载集度间的微分关系 二、q(x)、F S(x)图、M(x)图三者间的关系 三、分布荷载集度、剪力和弯矩之间的积分关系
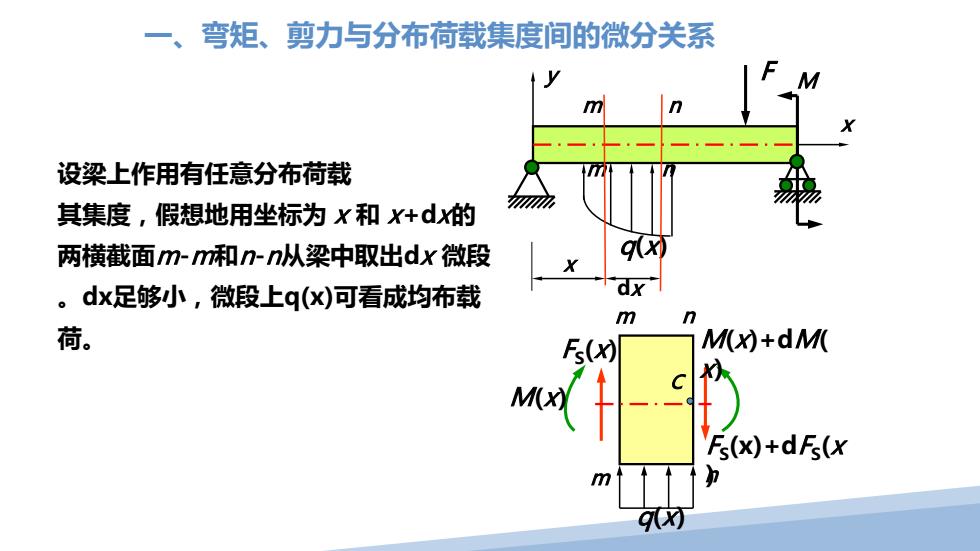
一、弯矩、剪力与分布荷载集度间的微分关系 设梁上作用有任意分布荷载 其集度,假想地用坐标为X和X+dX的 两横截面m-m和n-n从梁中取出dx微段 q(x) 。dx足够小,微段上q(x)可看成均布载 m 荷。 Fs(x) M(x)+dM( M(x) Fs(x)+dFs(x m 9材
x y q(x) F M F S(x) M(x) F S(x)+dF S(x ) M(x)+dM( x) 设梁上作用有任意分布荷载 其集度,假想地用坐标为 x 和 x+dx的 两横截面m-m和n-n从梁中取出dx 微段 。dx足够小,微段上q(x)可看成均布载 荷。 m m n n q(x) C n x m m n dx 一、弯矩、剪力与分布荷载集度间的微分关系
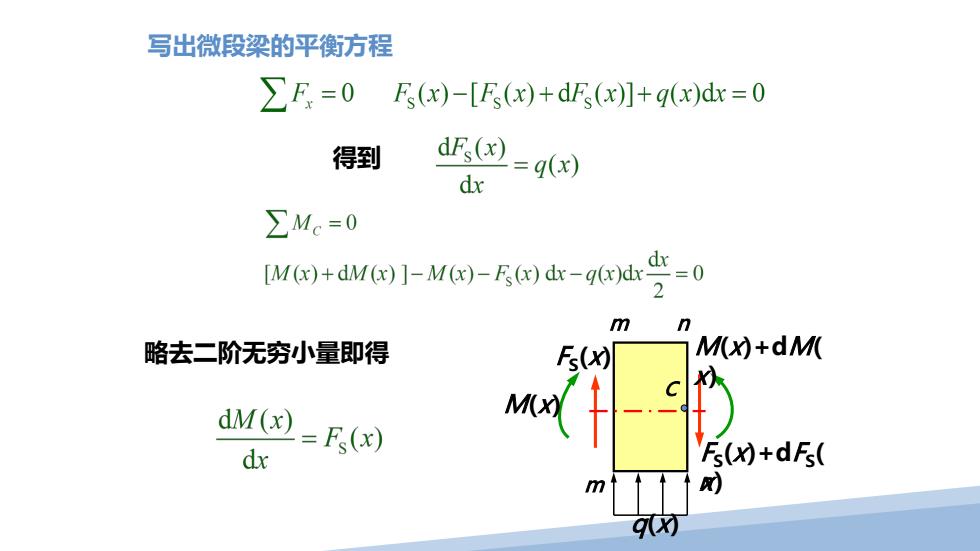
写出微段梁的平衡方程 ∑F=0 F(x)-[E(x)+dF(x)]+q(x)d=0 得到 dF(x) dx =q( ∑Me=0 [MG)+dM()]-M()-F;(x)dx-g()dx 2 m n 略去二阶无穷小量即得 Fs(x) M(x)+dM( dM(x)=Fg(x) M dx Fs(x)+dFs( m 财 9方
F S(x) M(x) F S(x)+dF S( x) M(x)+dM( x) m m n n q(x) C 写出微段梁的平衡方程 得到 略去二阶无穷小量即得

dFs(x dx .-q(x) dM(x)=Fs(x) dx d'M(x)-q(x) 公式的几何意义 dx2 (1)剪力图上某点处的切线斜率等于该点处荷载集度的大小; (2)弯矩图上某点处的切线斜率等于该点处剪力的大小; (3)根据g)>0或g)<0来判断湾矩图的凹凸性
公式的几何意义 (1)剪力图上某点处的切线斜率等于该点处荷载集度的大小; (2)弯矩图上某点处的切线斜率等于该点处剪力的大小; (3)根据q(x)>0或q(x) <0来判断弯矩图的凹凸性
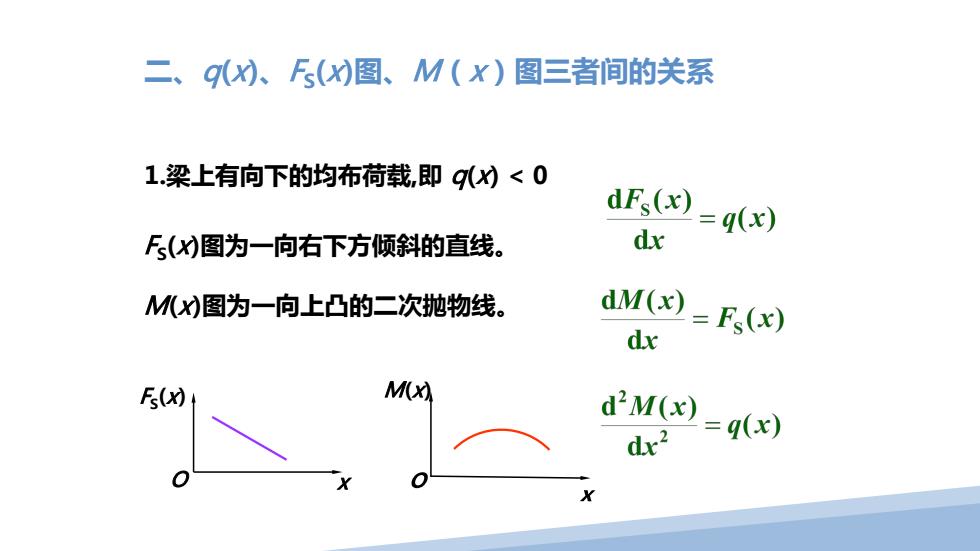
二、g)、F()图、M(x)图三者间的关系 1梁上有向下的均布荷载,即g(x)<0 dFs(x) dx =q(x) F()图为一向右下方倾斜的直线。 MX)图为一向上凸的二次抛物线。 dM(x)=Fs(x) dx Fs(x) M(x) d2M(x dx2 =q(x X
M(x)图为一向上凸的二次抛物线。 F S(x)图为一向右下方倾斜的直线。 x F S(x) O 二、q(x)、F S(x)图、M(x)图三者间的关系 1.梁上有向下的均布荷载,即 q(x) < 0 M(x)