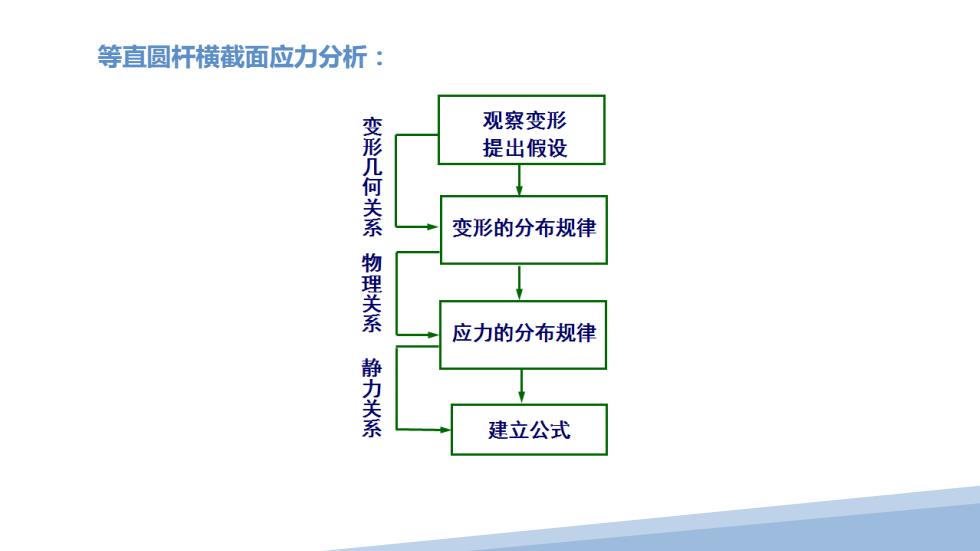
等直圆杆横截面应力分析: 观察变形 提出假设 变形几何关系物理关系 变形的分布规律 应力的分布规律 静力关系 建立公式
等直圆杆横截面应力分析:

一、等直圆杆扭转实验观察: 17 1.横截面变形后仍为平面,、 半径仍保持直线; dx 2.轴向无伸缩,两截面间距 (圆轴扭转的平面假设) 离不变;(无正应力) 3.纵向线变形后仍为平行
1. 横截面变形后仍为平面, 半径仍保持直线; 2. 轴向无伸缩,两截面间距 离不变; 3. 纵向线变形后仍为平行。 一、等直圆杆扭转实验观察: (无正应力) (圆轴扭转的平面假设)
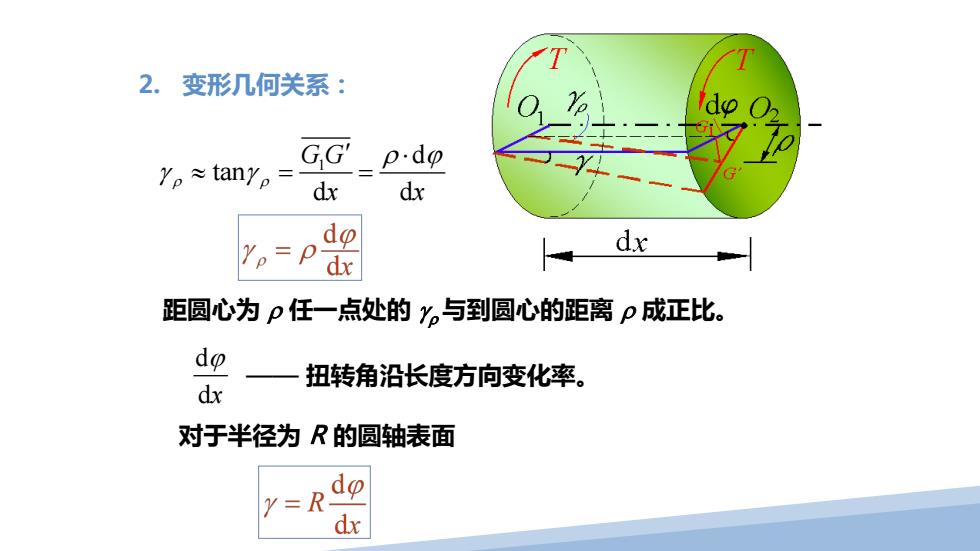
2.变形几何关系: G,G' p.do Yp≈tanye= dx dx do dx 距圆心为p任一点处的y。与到圆心的距离p成正比。 do 扭转角沿长度方向变化率。 dx 对于半径为R的圆轴表面 Y= do dx
2. 变形几何关系: 1 d tan d d G G x x ρ ρ ρ ϕ γ γ ′ ⋅ ≈ == 距圆心为 ρ 任一点处的 γρ 与到圆心的距离 ρ 成正比。 d dx ϕ —— 扭转角沿长度方向变化率。 对于半径为 R 的圆轴表面
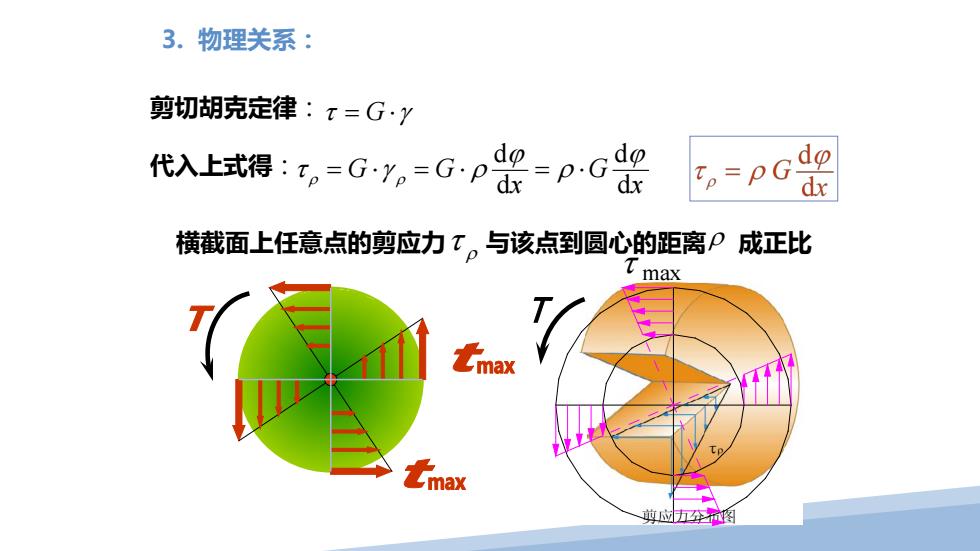
3.物理关系: 剪切胡克定律:t=G·Y pg=pG器 代入上式得:t,=G·y,=G tp=PG d dx 横截面上任意点的剪应力T。与该点到圆心的距离P成正比 T max max max 剪应☑图
3. 物理关系: 剪切胡克定律: 代入上式得: τ = G ⋅γ x G x G G d d d d ϕ ρ ϕ τ ρ = ⋅γ ρ = ⋅ ρ = ⋅ 横截面上任意点的剪应力 τ ρ 与该点到圆心的距离 ρ 成正比 τ max T
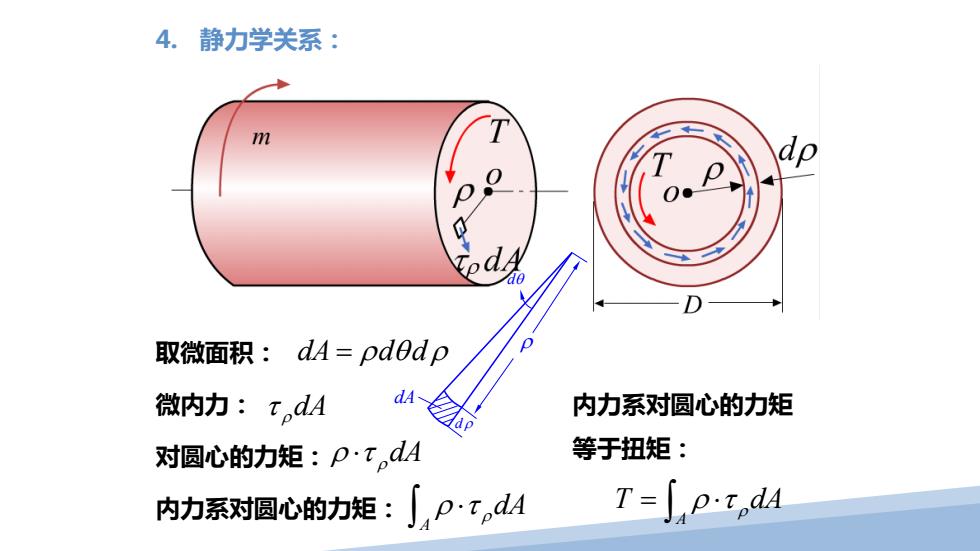
4.静力学关系: m 取微面积:dA=pdodp 微内力:t,dA 内力系对圆心的力矩 对圆心的力矩:p·t,dA 等于扭矩: 内力系对圆心的力矩:∫,ptdA T=∫pt,dA
4. 静力学关系: 取微面积: dA d d = ρθ ρ 微内力: τ ρdA 对圆心的力矩:ρ τ⋅ ρdA 内力系对圆心的力矩: A ρ τ⋅ ρdA ∫ 内力系对圆心的力矩 等于扭矩: A T dA = ⋅ ∫ ρ τ ρ dθ ρ dρ dA