
x2-y2=a2. 此轨迹为双曲线x2-v2=a2. (10)1z1+3212+|z1-22|2=2|3,2+2122{2. 解:这是一个恒等式,对于复平面上任意的之和22都成立, 因为 ,+222+121-2212=(x1+x2)2+(y1+y2)2 +(x,-x2)+(y,-y2)2 =2×12+2x22+2y12+2y22 =21z1|2+212212. 它表示平行四边形对角线的平方 和等于两邻边平方和的两倍. 此外,如把z1和z2表示成复 平面上的矢量,那么之1和2的加 减运算与相应的矢量的加减运算 (平行四边形法则)是相同的,。 这可由图1-2清楚地看出. 图1-2 2.把下列复数用代数式、三角式和指数式几种形式表示出 来。 (1)i. 解:i本身即为代数式,此时在2=x+y中,x=0、 y=1, 三角式:p=Jx2+y2=1, p=aretg()=argtg(日)=号, 所以2=i=cos+isin 指数式:2=4=e受

(2)-1. 解:一1本身即为代数式, 三角式:2=cosπ+isina, 指数式:2=e", (3)1+3 解:2=1+√3本身即为代数式, 三角式1。-+5ae2:p=arcg臣=号, 1 所以 2-2(cos子+sin牙)为 指数式:2=2e分. (4)1-cosa+isina(a是实常数), 解:2=(1-cosa)+isinax本身即为代数式, 三角式:p=J(1-cosa)2+sin2a=2(1-cosa) =2sin-2 aret uct sina (+》名, 在主值范围内0=之(a-a)(0<a<),所以 sin 2 cos(aretgetg 2) +sin(arotgetg 2-》

或 2=2sim名(cos”22+sin“22) (0≤a≤π): 指数式。=2sin兰号, 。2ie(2 (5)23. 解:代数式:z3=(×+y)3=(x3-3xy2)+i(3x2y-y) 三角式:z3=p3(cos3p+isin3p), 其中p=J2+少,m=arctg(): 指数式:23=pe". (6)e1+i. 解:指数式即为2=e1+1=ee',显然,其中p=.e,p= 1, 三角式:2=e(cos1+isin1); 代数式:2=ecos1+iesinl. ) 期,代数试g宁1-0-i 三角式:因p=1,0=aot(0)=受,所以 指数式:2=e受. 3.计算下列数值(a、b和p为实常数)·
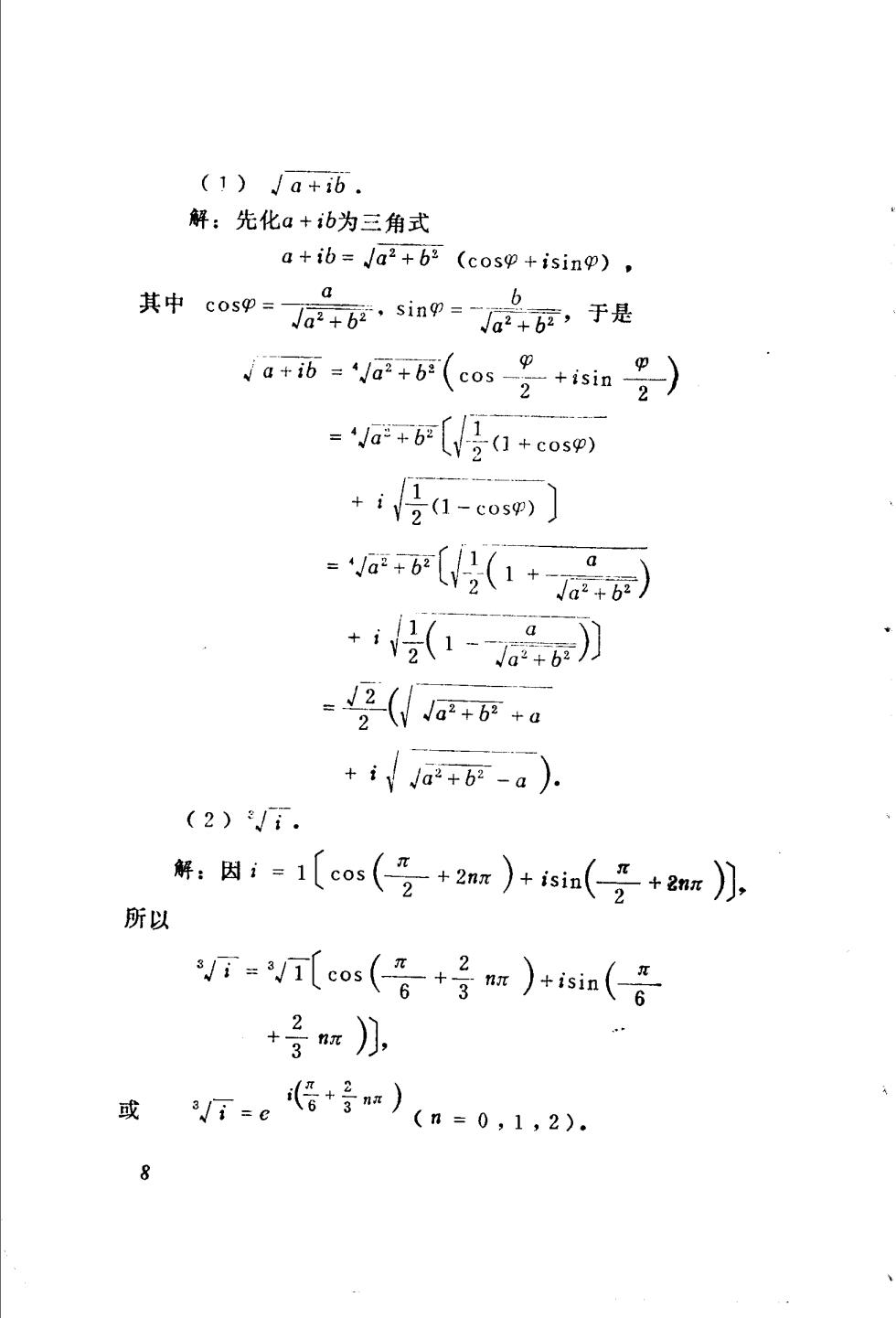
(1)Ja+b. 解:先化a+b为三角式 a+ib=Ja2+b (cosp+isin), 其中cos9=后后,sin0=a”石,于是 a*6=0+6(cog+isin) ='a+6(/经a+cosP) +i日1-e0s0)〕 o1+) +(1os》 (F+a +ia2+b-a). (2). 解:因i=1〔cos(空+2nr)+sin(交+2mr】, 所以 =可cos(g+号r)+sia(g +子m月, 或行=e6*号)(a0,1,2

(3), 解:因:=e(号+2x),所以 i=〔e(经+2m]=e-受-2mn(n=0,±1,±2,.) (4)Ji. 解:仿上题、 万e经a:e音*(n0.±1,±2,. (5)cos5. (6)sin5p. 解:由乘幂的公式 (cose +isin)"=cosno+isinnp, 及二项式定理 u+b)"=a°+ma-1hkn,1八a-62+., 21 +m-1!a6+ n! 可知 cos5o +isin50=(coso +ising) =cos5o +i5cososino -10cos3osin'g -il0cos2gsin +5cosysin'p +isinsp, 比较等式两边的实部和虚部得 cos5o coso-10cos3sin20+5cosesin'o, sin5p=5cos'sin-10cos2psin3+sino. 7 coso+cos2p+cos30+.+cosno. (8)sinp+sin2p+sin3p+.+sinng