
例:求图示电路中各方 框所代表的元件吸收或 产生的功率。已知: 0=1V,U2=-3V, U3=8V,U4=-4V, U5=7V,U6=-3V, I1=2A,I2=1A,I3=-1A 解:P1-UH=IX2=2w,户度=以3)X2=-6w P3吸=U31=8X2=16W;P4吸=U4l2=(-4)X1=-4W Ps吸=U13=7X(1)=-7W;P6吸=U63=(-3)X(-1)=3W 8对一完整电路,满足:发出的功率=吸收的功率
6 例:求图示电路中各方 框所代表的元件吸收或 产生的功率。已知: 解: U1=1V,U2= -3V, U3=8V,U4= -4V, U5=7V,U6= -3V, I1=2A,I2=1A,I3= -1A P1发=U1 I1=1×2 =2W; P2吸=U2 I1=(-3)×2 = -6W P3吸=U3 I1=8×2=16W;P4吸=U4 I2=(-4)×1 = -4W P5吸=U5 I3=7×(-1) = -7W;P6吸=U6 I3=(-3)×(-1) = 3W 对一完整电路,满足:发出的功率=吸收的功率 5 6 4 1 2 3 I2 I3 I1 + + + + + + - - - - - U6 U U5 4 U3 U2 U1

3.理想电源元件(source) 电压源 实际电源 电源 电流源 理想电压源 E①(R=0) 理想电源 理想电流源 ⊙(R一o) 受控电源
受控电源 理想电压源 电源 实际电源 理想电源 电压源 理想电流源 电流源 Is R0 U0 E + _ U0 R0 E (R0 =0) Is (R0 ∞) 3. 理想电源元件 (source)
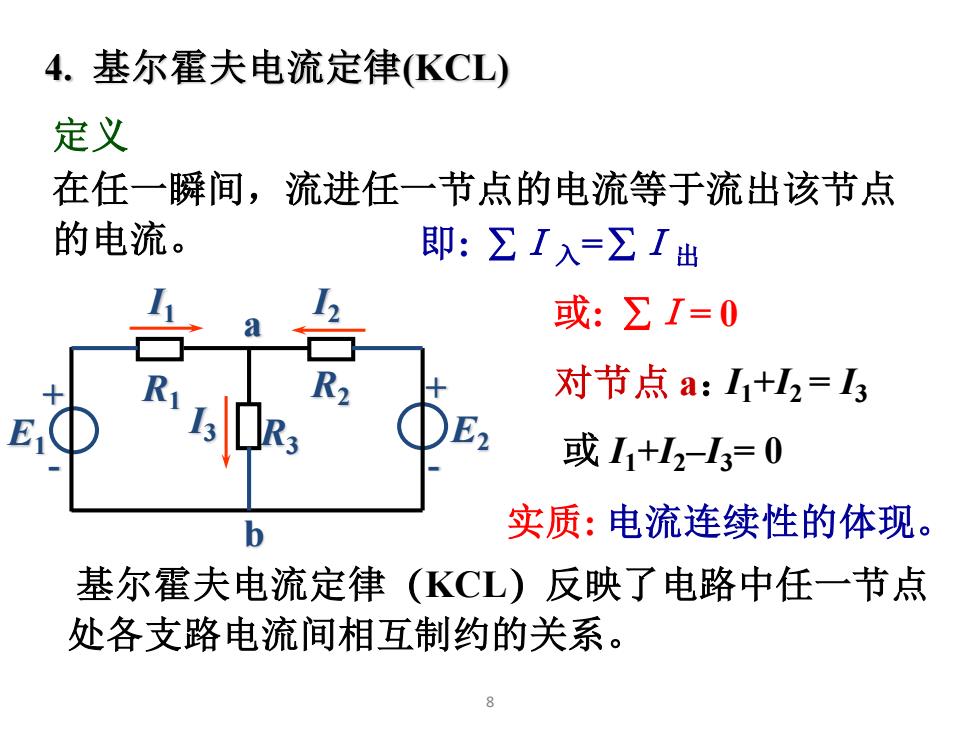
4.基尔霍夫电流定律(KCL) 定义 在任一瞬间,流进任一节点的电流等于流出该节点 的电流。 即:∑I入=∑I出 或:∑I=0 对节点a:I1+2=3 或I1+12-3=0 实质:电流连续性的体现。 基尔霍夫电流定律(KCL)反映了电路中任一节点 处各支路电流间相互制约的关系
8 4. 基尔霍夫电流定律(KCL) 定义 即: I入=I出 在任一瞬间,流进任一节点的电流等于流出该节点 的电流。 实质: 电流连续性的体现。 或: I= 0 对节点 a:I1+I2 = I3 或 I1+I2–I3= 0 基尔霍夫电流定律(KCL)反映了电路中任一节点 处各支路电流间相互制约的关系。 b a + - E2 + R2 - R3 R1 E1 I1 I2 I3
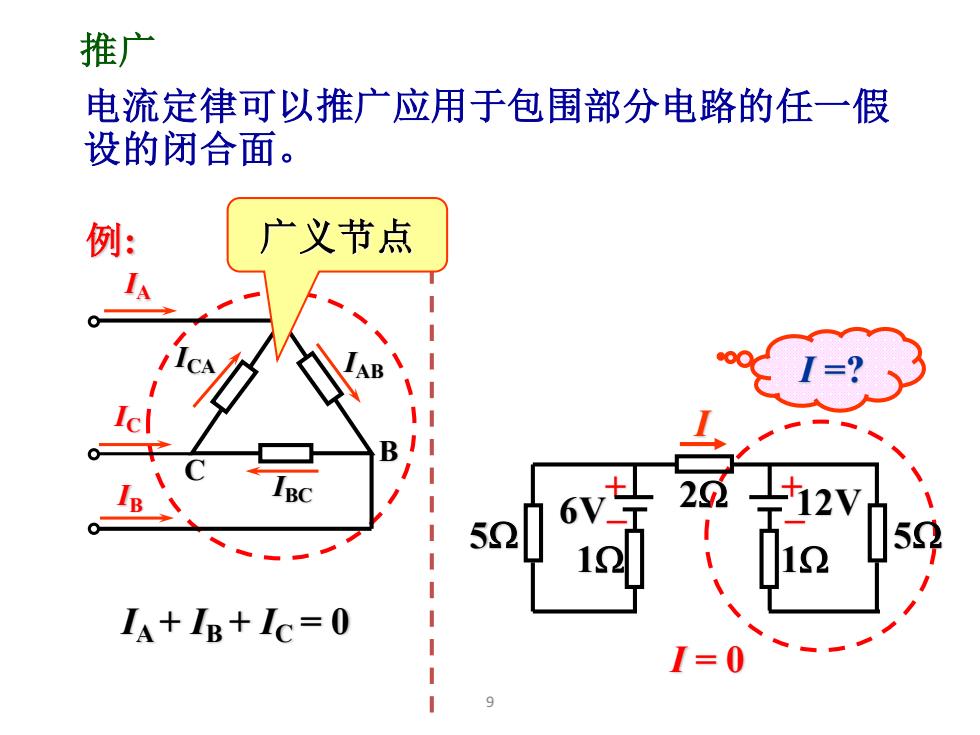
推广 电流定律可以推广应用于包围部分电路的任一假 设的闭合面。 广义节点 IA+IB+Ic=0
9 电流定律可以推广应用于包围部分电路的任一假 设的闭合面。 推广 I =? 例: I = 0 IA + IB + IC = 0 2 + _ + _ I 5 1 1 5 6V 12V IA IB ICA IBC IAB A C B IC 广义节点
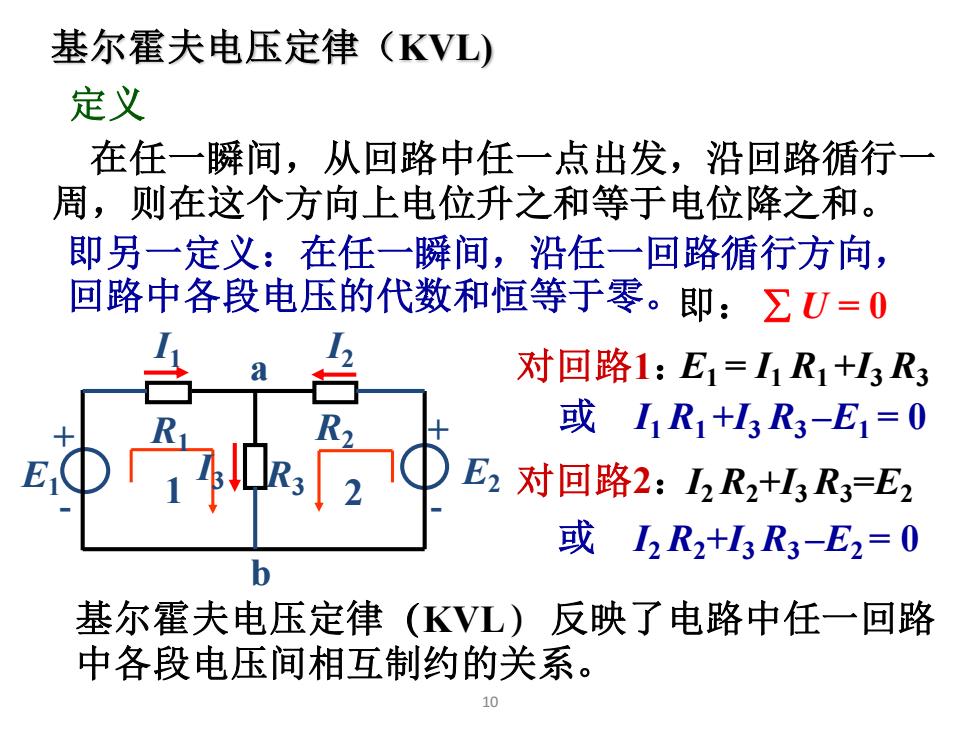
基尔霍夫电压定律(KVL) 定义 在任一瞬间,从回路中任一点出发,沿回路循行一 周,则在这个方向上电位升之和等于电位降之和。 即另一定义:在任一瞬间,沿任一回路循行方向, 回路中各段电压的代数和恒等于零。即:ΣU=0 对回路1:E1=I1R1+IR3 或I1R1+山3R3-E1=0 E2对回路2:2R2+H3R3-E2 或I2R2+I3R3-E2=0 基尔霍夫电压定律(KVL)反映了电路中任一回路 中各段电压间相互制约的关系。 10
10 即另一定义:在任一瞬间,沿任一回路循行方向, 回路中各段电压的代数和恒等于零。 基尔霍夫电压定律(KVL) 定义 即: U = 0 在任一瞬间,从回路中任一点出发,沿回路循行一 周,则在这个方向上电位升之和等于电位降之和。 对回路1: 对回路2: E1 = I1 R1 +I3 R3 I2 R2+I3 R3=E2 或 I1 R1 +I3 R3 –E1 = 0 或 I2 R2+I3 R3 –E2 = 0 1 2 基尔霍夫电压定律(KVL) 反映了电路中任一回路 中各段电压间相互制约的关系。 I1 I2 I3 b a + - E2 + R2 - R3 R1 E1