
取每火二分小区间的中点可得一个收敛序列{化片,该实教序列的极 就是方程的根。即lmXm=xo n-→+00 -a
取每次二分小区间的中点可得一个收敛序列 n i i x =1 ,该实数序列的极 就是方程的根。即 * lim x x n n = →+ 。 n n b a x x 2 * − − 若要求精度 − n x x * ,则要做等分区间的次数至少是: log 2 +1 − b a
erfengfaqiujie.m a=5;b=6,x1=a,x2=b: while abs(x1-x2)>0.000001 x3=(x1+x2)/2: f3=4*cos(x3)+4*sin(x3)+0.5*x3-2; if f3~=0 f1=4*cos(x1)+4*sin(x1)+0.5*x1-2; .12 f2=4*cos(x2)+4*sin(x2)+0.5*x2-2; 10 20 25 30 if fl*f3<0 ★计算5<0<6内的交点 X2=x3; else Matlab x1=x3; 实际上: 查看图形 end f(5)=-2.20104835679965 end end f(6)=3.72301915380576 x3 f'(0)=4(cos0-sinθ)+0.5>0 执行结果为:x3=5.37587451934814 该点的近似坐标为: (2.46346668293075,-3.15140157740808,5.37587451934814) continue
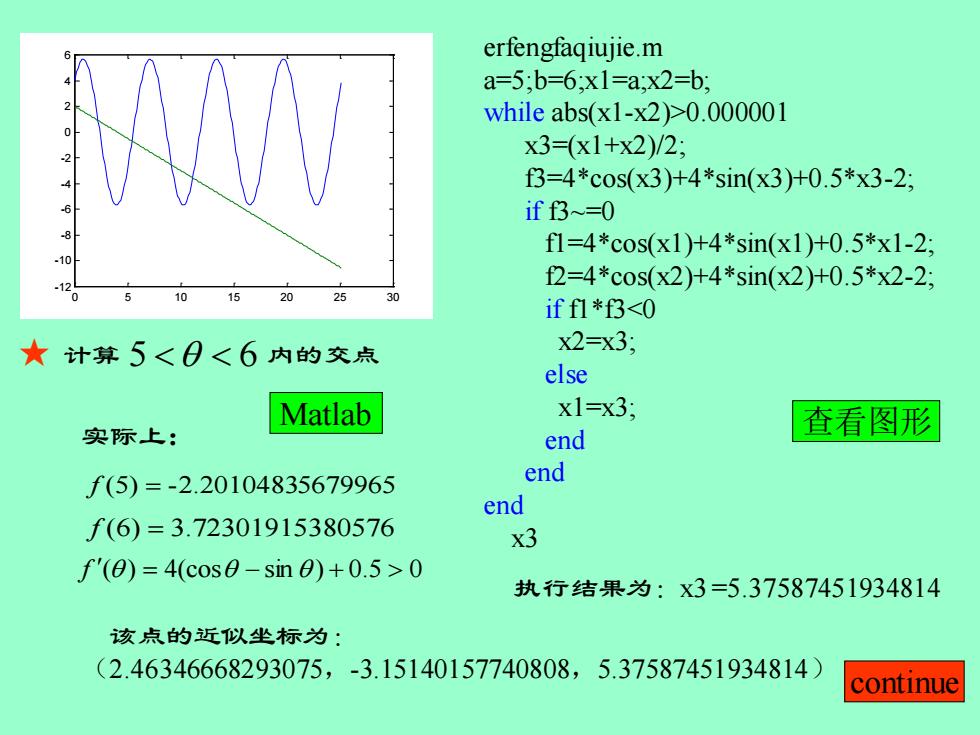
0 5 10 15 20 25 30 -12 -10 -8 -6 -4 -2 0 2 4 6 ★ 计算 5 6 内的交点 Matlab 实际上: f (5) = -2.20104835679965 f (6) = 3.72301915380576 f ( ) = 4(cos − sin ) + 0.5 0 erfengfaqiujie.m a=5;b=6;x1=a;x2=b; while abs(x1-x2)>0.000001 x3=(x1+x2)/2; f3=4*cos(x3)+4*sin(x3)+0.5*x3-2; if f3~=0 f1=4*cos(x1)+4*sin(x1)+0.5*x1-2; f2=4*cos(x2)+4*sin(x2)+0.5*x2-2; if f1*f3<0 x2=x3; else x1=x3; end end end x3 执行结果为:x3 =5.37587451934814 该点的近似坐标为: (2.46346668293075,-3.15140157740808,5.37587451934814) 查看图形 continue

30 25 20 15 10 0 0 -2 y -4 X Matlab back
back -4 -2 0 2 4 -4 -2 0 2 4 0 5 10 15 20 25 30 x轴 y轴 z轴 Matlab

(2)牛顿选代法 设方程f(x)=0有实数根,若能够将方程等价地转化成X=8(x), 取一个初始值X0代入x=8(x)的右端算得X1=8(X),依次再计算 X2=g(x),类推可得序列x’ +0 k+1=8(xk),k=0,12,. 称此序列为由迭代函数8(X)产生的迭代序列,X。为迭代初始值。 若该迭代序列收敛,则它的极限就是方程∫(x)=0的一个根。Xk 称为方程根的k次近似值.称使得迭代法收敛的初始值的取值范围为迭 代收敛域。 图示点击 例3.1容易验证方程x2+X-3=0有两个不相等的实数根。 输入MATLAB软件命令solv(x2+X-3=0)执行结果为: ans=【-1/2+1/2*13^(1/2] [1/2-1/2*13(1/2)] 该方程可等价地转化为X=3一x2,由此而决定的迭代格式为 Xk41=3-x2,k=0,12,3 continue
(2) 牛顿迭代法 设方程 f (x) = 0 有实数根,若能够将方程等价地转化成 x = g(x) , 取一个初始值 0 x 代入 x = g(x) 的右端算得 ( ) 1 0 x = g x ,依次再计算 ( ) 2 1 x = g x ,类推可得序列 ( ) k 1 k x = g x + , k = 0,1,2, + k k=1 x , 称此序列为由迭代函数 g(x) 产生的迭代序列, 0 x 为迭代初始值。 若该迭代序列收敛,则它的极限就是方程 f (x) = 0 的一个根 。 k x 称为方程根的k次近似值.称使得迭代法收敛的初始值的取值范围为迭 代收敛域。 图示点击 例3.1 容易验证方程 3 0 2 x + x − = 有两个不相等的实数根。 输入MATLAB软件命令solve(‘x^2+x-3=0’) 执行结果为: ans = [ -1/2+1/2*13^(1/2)] [ -1/2-1/2*13^(1/2)] 该方程可等价地转化为 2 x = 3 − x ,由此而决定的迭代格式为 2 k 1 3 k x = − x + ,k = 0,1,2,3 continue