
五.转动定律的应用举例 例一轻绳绕在半径r=20cm的飞轮边缘,在绳端施以F=98N 的拉力,飞轮的转动惯量J=0.5kgm,飞轮与转轴间的摩擦 不计,(见图) 之LI 求(1)飞轮的角加速度 (2)如以重量P=98N的物体挂在绳 端,试计算飞轮的角加速 解(1)F=Jβ p=乃_98×0.2 0.5 -=39.2 rad/s2 mg (2)mg-T=ma mgr 两者区别 Tr=JB +mr a=rB 98×0.2 =21.8rad/s2 0.5+10×0.22
F Or (1) 飞轮的角加速度 (2) 如以重量P =98 N的物体挂在绳 端,试计算飞轮的角加速 解 (1) Fr = J 2 39 2 rad/s 0 5 98 0 2 . . . = = = J Fr (2) mg −T = ma Tr = J a = r 两者区别 五. 转动定律的应用举例 mgT 例 求 一轻绳绕在半径r =20 cm 的飞轮边缘,在绳端施以F=98 N 的拉力,飞轮的转动惯量J=0.5 kg·m2,飞轮与转轴间的摩擦 不计, (见图) 2 J mr mgr + = 2 2 21 8 rad/s 0 5 10 0 2 98 0 2 . . . . = + =
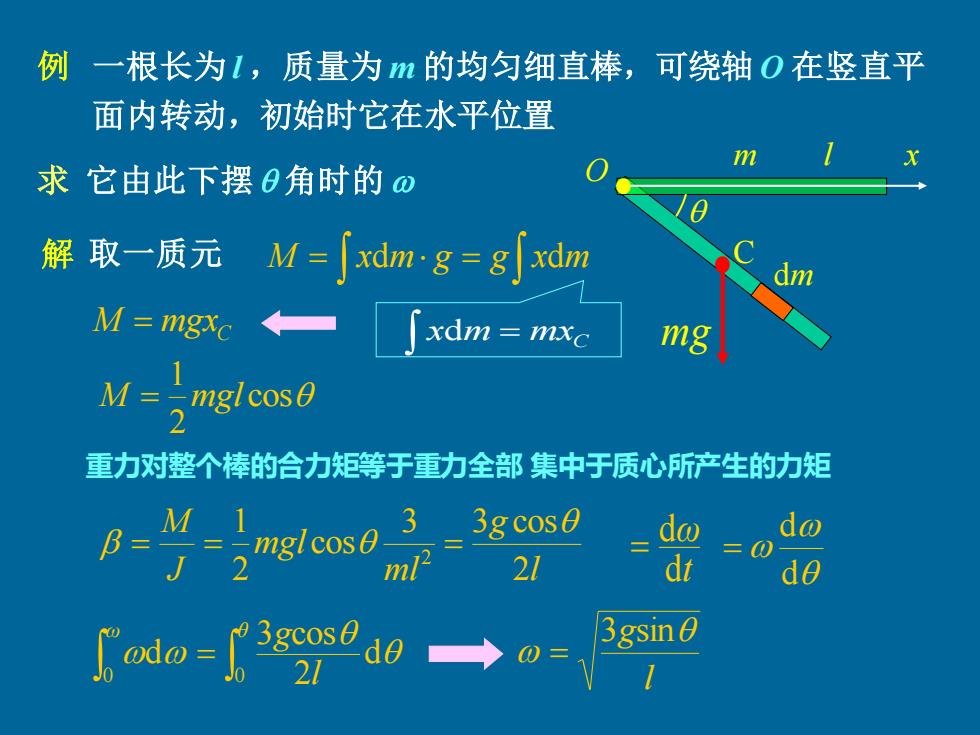
例 :一根长为1,质量为m的均匀细直棒,可绕轴O在竖直平 面内转动,初始时它在水平位置 求它由此下摆θ角时的o 解取一质元 M= xdmg=g xdm M=mgxc xdm=mxc mg M=-mgl cos0 重力对整个棒的合力矩等于重力全部集中于质心所产生的力矩 mglcos0-3 M.1 3g cos0 do =0 2 21 dt do 0do=1 3gsin 0 0三
一根长为 l ,质量为 m 的均匀细直棒,可绕轴 O 在竖直平 面内转动,初始时它在水平位置 求 它由此下摆 角时的 O m l C x 解 取一质元 M = xdm g = g xdm xdm = mxC M = mgxC 重力对整个棒的合力矩等于重力全部 集中于质心所产生的力矩 dm cos 2 1 M = mgl l g ml mgl J M 2 3 3 cos cos 2 1 2 = = = t ω d d = d d = mg = ω θ l g 0 0 d 2 3 cos d l g 3 sin = 例 • •
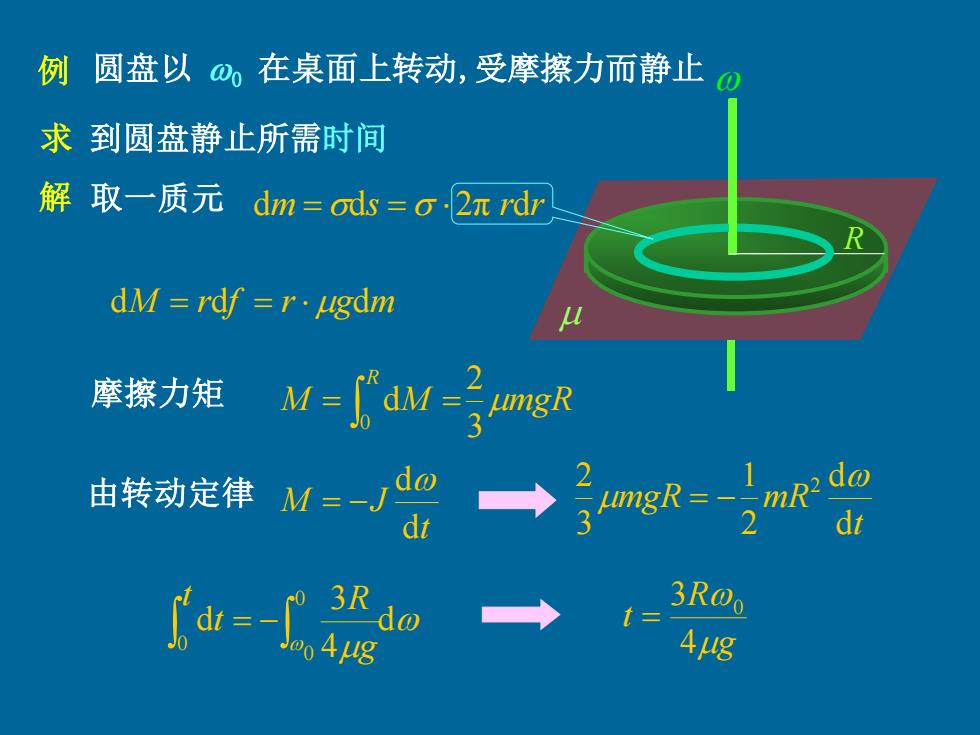
例圆盘以在桌面上转动,受摩擦力而静止心 求到圆盘静止所需时间 解取一质元dm=ods=o2πrdr dM=rdf =r.ugdm 摩擦力矩 M= dM=jmgR 由转动定律M=-J do 3tmgR-mR:do → do 3R@o Aug
圆盘以 0 在桌面上转动,受摩擦力而静止 解 dm =ds = 2π rdr dM = rdf = r gdm M M mgR R 3 2 d 0 = = t M J d d = − t mgR mR d d 2 1 3 2 2 = − d 4 3 d 0 0 0 = − g t R t g R t 4 3 0 = 例 求 到圆盘静止所需时间 取一质元 由转动定律 摩擦力矩 R