
理论推证 取一质量元万+子=m,a 切线方向 Fir+fir=mai 对固定轴的力矩 F+=ma =mB 对所有质元 ∑FH,+∑/,=(∑mp 合外力矩M 合内力矩=0 刚体的转动惯量J
O i r Fi i f • 理论推证 i i miai F f 取一质量元 + = i i i i 切线方向 F + f = m a i i i i i i i F r f r m a r 对固定轴的力矩 + = 2 i i = m r 对所有质元 + = ( ) 2 i i i i i i F r f r m r 合外力矩 M 合内力矩 = 0 刚体的转动惯量J • mi

三.转动惯量 定义式 J=△m, 质量不连续分布 J= r2dm 质量连续分布 ●计算转动惯量的三个要素:(1)总质量(2)质量分布(3)转轴 的位置 (1)J与刚体的总质量有关 例如两根等长的细木棒和细铁棒绕端点轴转动惯量 ML J铁>J木 dx
三. 转动惯量 = 2 i i 定义式 J m r 质量不连续分布 J = r 2 dm 质量连续分布 计算转动惯量的三个要素:(1)总质量(2)质量分布(3)转轴 的位置 (1) J 与刚体的总质量有关 例如两根等长的细木棒和细铁棒绕端点轴转动惯量 L z O x dx 2 M 0 2 0 2 3 1 d dx ML L M J x x x L L = = = J铁 J木 •
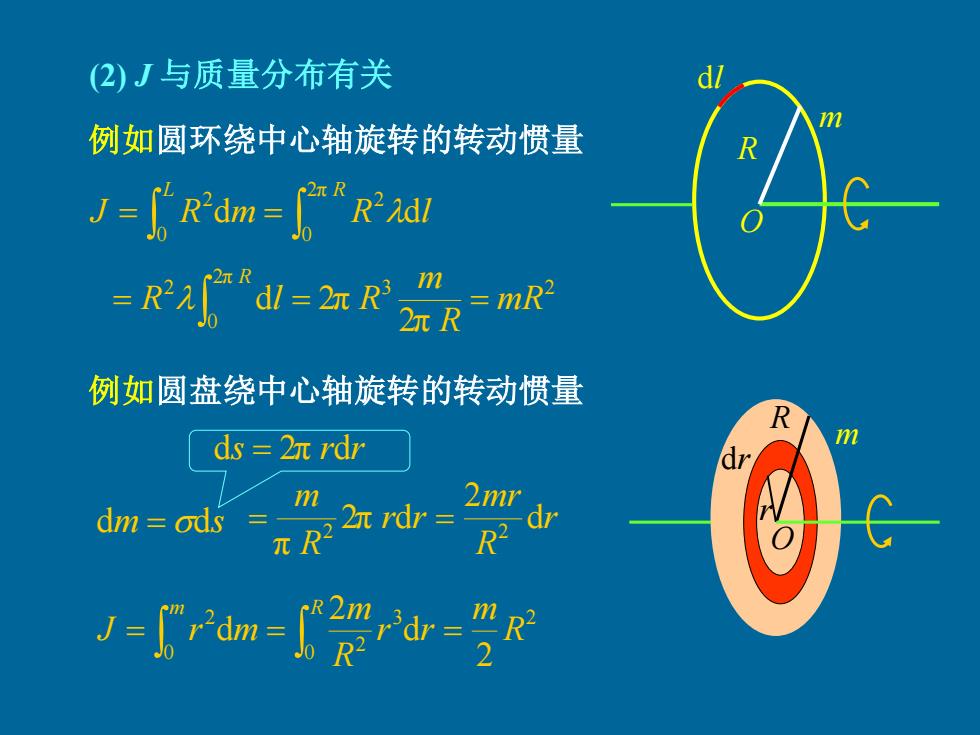
(2)J与质量分布有关 例如圆环绕中心轴旋转的转动惯量 JR'dm=R'ndl =Rd-2 m =mR2 例如圆盘绕中心轴旋转的转动惯量 ds 2n rdr m 2n rdr= 2m dm ods 三 x R2 J=r7dm=20
(2) J 与质量分布有关 例如圆环绕中心轴旋转的转动惯量 例如圆盘绕中心轴旋转的转动惯量 dl = = O L R J R m R l 2π 0 2 0 2 d d 3 2 2π 0 2 2π d 2π mR R m R l R R = = = m R O m r dr ds = 2π rdr dm = ds = = = m R R m r r R m J r m 0 3 2 2 0 2 2 d 2 d r R mr r r R m d 2 2π d π 2 2 = = R
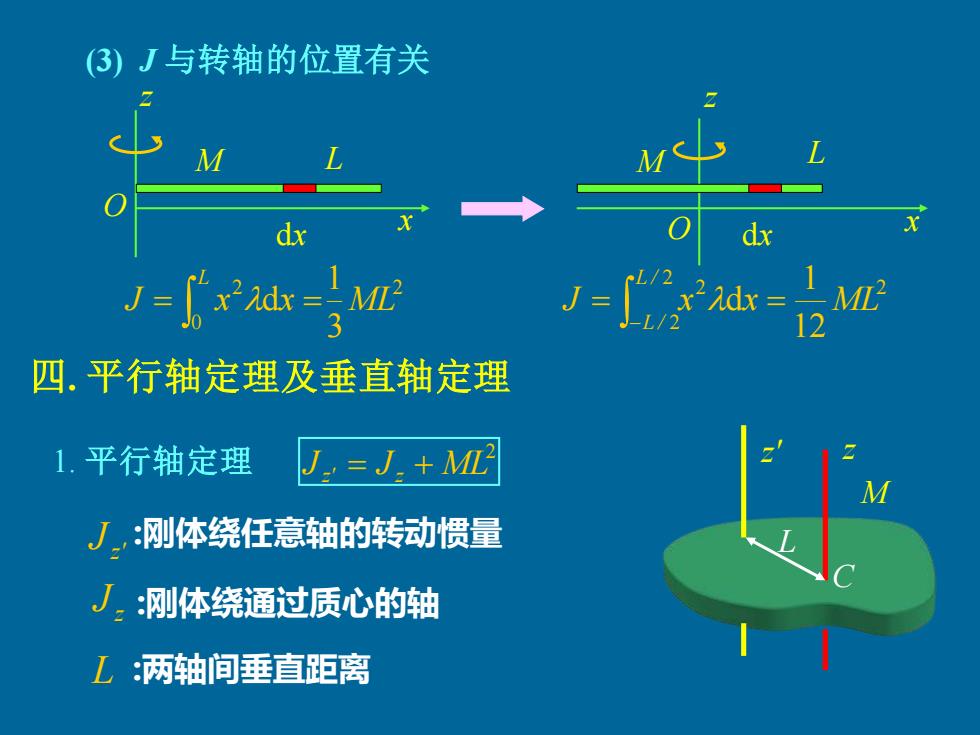
(3)J与转轴的位置有关 d dx [x"Adx =MI 四.平行轴定理及垂直轴定理 1.平行轴定理 J.=J.+ML J.,:刚体绕任意轴的转动惯量 J:刚体绕通过质心的轴 乙:两轴间垂直距离
O L x dx M z 2 0 2 3 1 J x dx ML L = = L O x dx M 2 2 2 2 12 1 J x dx ML L / L / = = − 四. 平行轴定理及垂直轴定理 z L C M ML2 z' J J z' = z + z (3) J 与转轴的位置有关 1. 平行轴定理 z' J z J L :刚体绕任意轴的转动惯量 :刚体绕通过质心的轴 :两轴间垂直距离
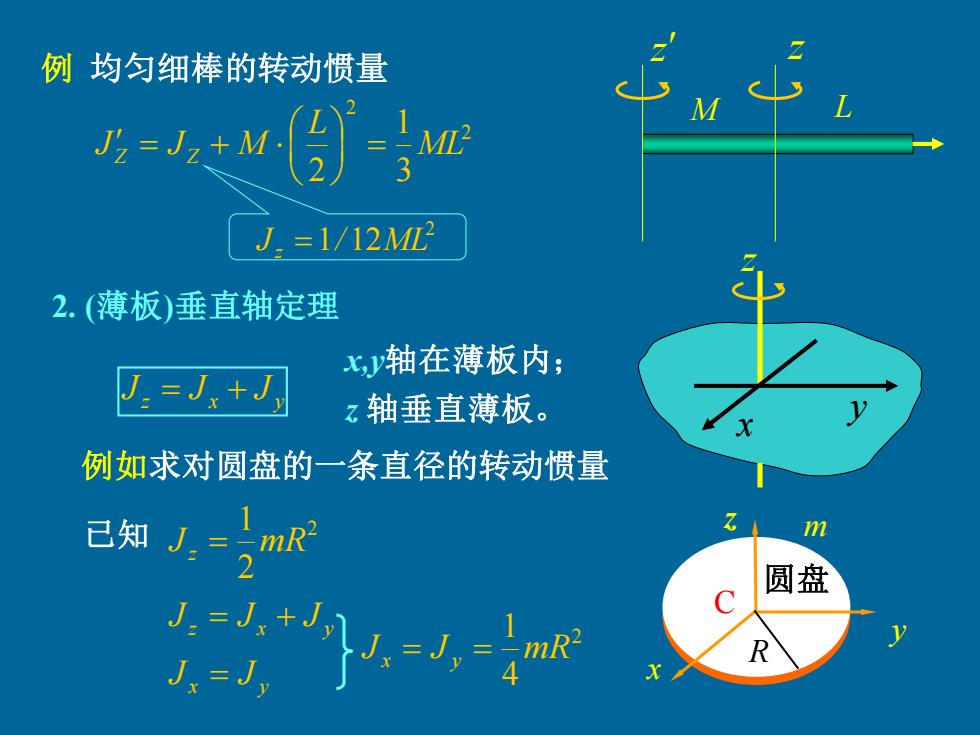
例均匀细棒的转动惯量 J2=Jz+M 2 M J.=1/12M 2.(薄板)垂直轴定理 x,轴在薄板内; J.=J+J z轴垂直薄板。 例如求对圆盘的一条直径的转动惯量 1 已知J=mR m 圆盘 √+山,=JmR R J=J
2 Jz =1/ 12ML 2 2 3 1 2 ML L JZ JZ M = = + 例 均匀细棒的转动惯量 2. (薄板)垂直轴定理 z x y J = J + J z M L z 例如求对圆盘的一条直径的转动惯量 2 2 1 Jz = mR z x y J = J + J x y J = J 已知 2 4 1 Jx = J y = mR y x z 圆盘 R C m x,y轴在薄板内; z 轴垂直薄板。 z x y