《机械工程控制基础》课程授课教案（讲义）第三章 系统的时域分析

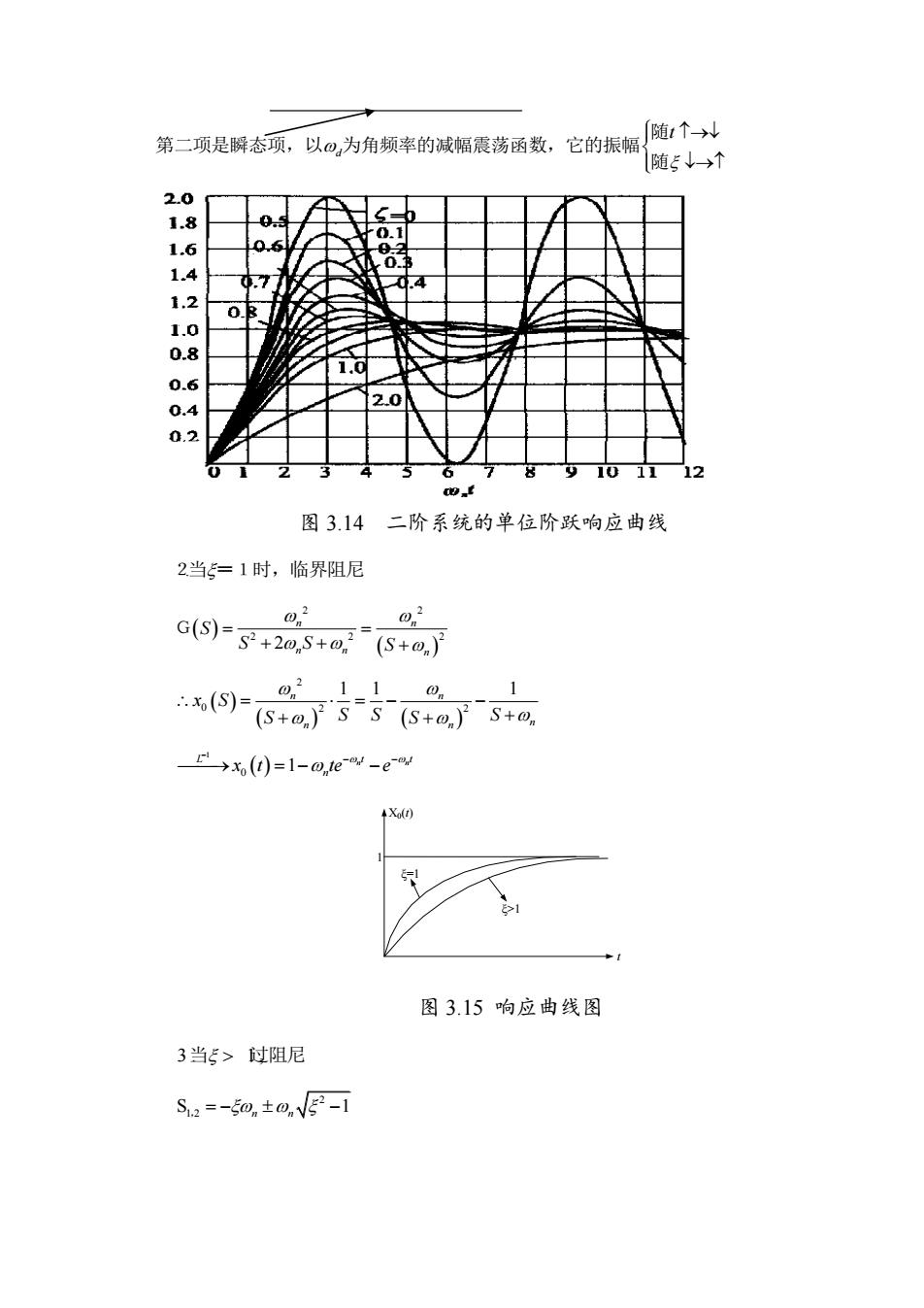
第二项是瞬态项，以@，为角领率的减幅震荡函数，它的振幅随1个→火 随ξ↓→↑ 2.00 1.8 1.2 1.0 0.8 0.6 2.0 0.4 0.2 12 图3.14二阶系统的单位阶跃响应曲线 2当=1时，临界阻尼 2 0,2 G(S)-s+205+0(S+0.) 0n21_10n x(例)-ss+s+a 1 →x,(0=1-oew-ew 图3.15响应曲线图 3当5>过阻尼 Sa=-50±a,@

d t        随 第二项是瞬态项，以 为角频率的减幅震荡函数，它的振幅 随 图 3.14 二阶系统的单位阶跃响应曲线 ２.当＝１时，临界阻尼     2 2 2 2 2 2 n n n n n S S S S           Ｇ       2 0 2 2 n n 1 1 1 n n n x S S S S S S                 1 0 1 n n L t t n x t te e           X0(t) t ξ=1 1 ξ>1 图 3.15 响应曲线图 3. 1, 当  过阻尼 2 S 1 1 2 n n ，       

@2 x侧5+a+as+a-F可3 12-52-552-1+利2-52-5-1+ ss+a,+a-s+50,-m,尽-可 →x(0=1 -可w 2-52-5®-1+可 2-52-5F-1+ 如上图，系统无超调，且过渡过程时间较长。 4当5=0倭阻尼 G6)= x,(S)S2+0 o211S 3(5)-G(S)x(S)-tos"550. →x,()=1-c0s/ 可见：系统为无阻尼等幅振荡 (1)欠阻尼的阶跃响应为衰减振荡，0，=0V-,5↓，@，↑（振荡幅度） (2)临界阻尼和过阻尼系统的阶跃响应均无超调，5个，过渡时间个（化，） (3)欠阻尼，=0.4-0.8，t,<t,(5=)且振荡不太严重。 (4)根据给定的性能指标设计系统时，通常选二阶。 二阶系统容易获得七，↓，且满足振荡性能要求 三、二阶系统的单位脉冲响应 x()=6()→x(S)=1x6()单位脉冲响应→o(0 W(S)-x(5)-G(5)-x(5)-G(S)-s+2m.S+0. 1.当0<5<时：欠阻尼系统 w(⑨S+m+a-安 )

     2 0 2 2 1 1 1 n n n n n X S S S S                    2 2 2 2 2 2 1 1 2 1 1 2 1 1 1 1 1 n n n n S S S                                        2 2 1 1 1 0 2 2 2 2 1 1 1 2 1 1 2 1 1 n n t t L x t e e                                如上图，系统无超调，且过渡过程时间较长。 4. 0. 当  零阻尼       2 0 2 2 n i n x S G S x S S            2 0 2 2 2 2 n 1 1 i n n S x S G S x S S S S S              1 0 1 cos L n x t t      可见：系统为无阻尼等幅振荡 （1）欠阻尼的阶跃响应为衰减振荡，   2 1 , ,      d n d     振荡幅度 （2）临界阻尼和过阻尼系统的阶跃响应均无超调，    ，过渡时间 t s  （3）欠阻尼，   =0.4 0.8 ~ 1 ，t t s s     且振荡不太严重。 （4）根据给定的性能指标设计系统时，通常选二阶。 二阶系统容易获得 t s  ，且满足振荡性能要求 三、二阶系统的单位脉冲响应                     0 2 0 2 2 1 W 2 i i n i n n x t t x S x t t S x S G S x S G S S S                  单位脉冲响应 1. 0 1 : 当    时 欠阻尼系统     2 2 2 W 1 d n n d S S               1 2 sin 1 n L n t d t e t            