《机械工程控制基础》课程授课教案（讲义）第三章 系统的时域分析

(3)经过3T-4T,达稳态值的95%98%，可认为其调整过程完成， 故一般取调整时间为(34)Ts (4)在0处，响应曲线的切线斜率：1/T 时间常数T反映了一阶系统的固有特性，T↓系统惯性↓系统响 应↑ 二、一阶系统的单位脉冲响应 x(0)=8()+x(S)=1 =1安 k0 表32一阶系统的单位脉冲响应表 t 0 T 2T 4T 0368013500181 0 4X) 你 0.368/T- 十27T行 图3.9响应曲线 <2%,过渡过程：，=4T调整时间T↓，过渡时间↓，快速性个 三、一阶系统的单位斜放响应-[Xs1 x()=1,→ x(5)-

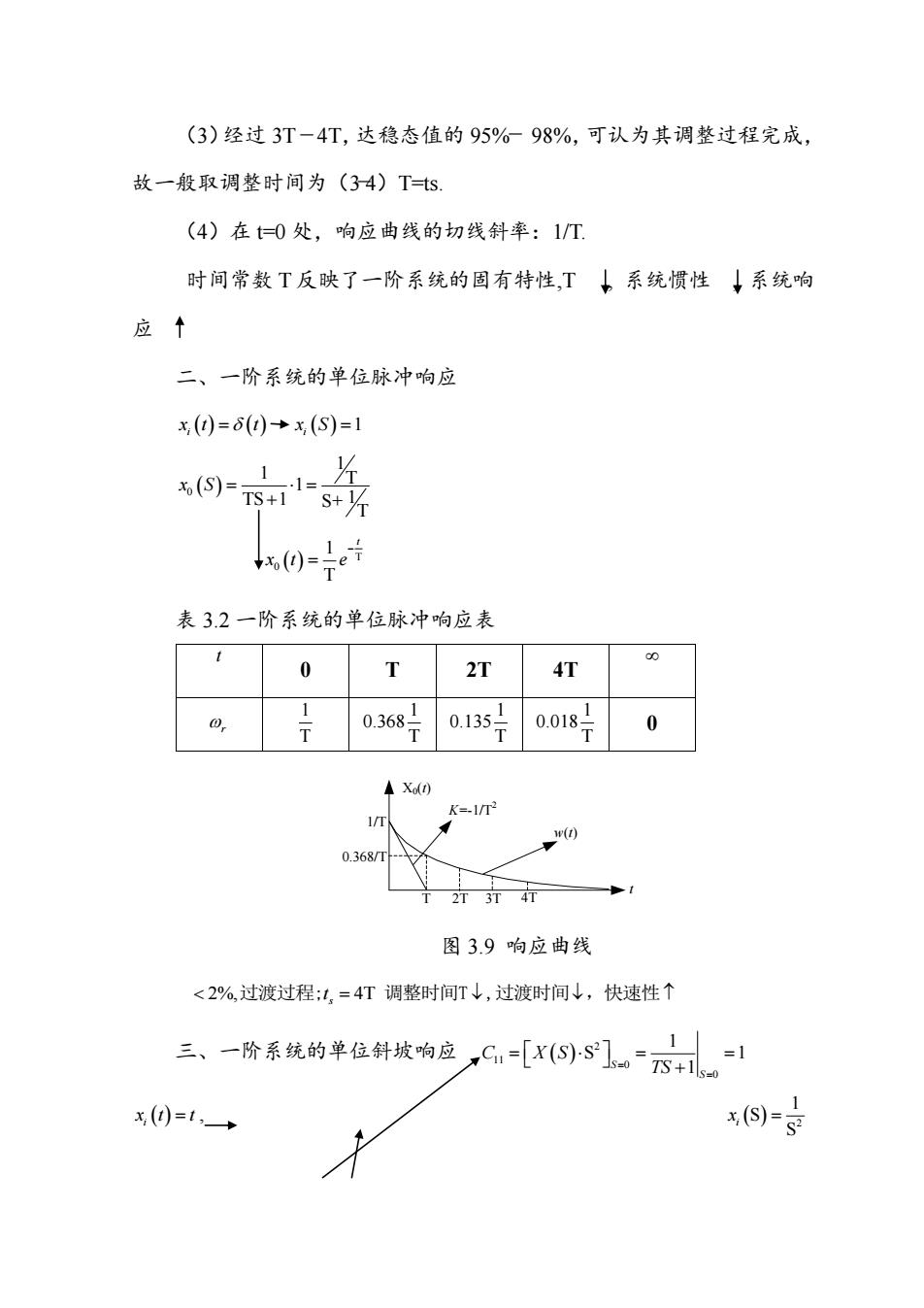
（3）经过 3T 4T，达稳态值的 95% 98%，可认为其调整过程完成， 故一般取调整时间为（3 4）T=ts. （4）在 t=0 处，响应曲线的切线斜率：1/T. 时间常数 T 反映了一阶系统的固有特性,T , 系统惯性 , 系统响 应 二、一阶系统的单位脉冲响应 x t t i         1 i x S  0   1 1 T 1 TS 1 S+ 1 T x S       T 0 1 T t x t e   表 3.2 一阶系统的单位脉冲响应表 t 0 T 2T 4T  r 1 T 1 0.368 T 1 0.135 T 1 0.018 T 0 X0(t) t 1/T 0.368/T T 2T 3T 4T K=-1/T2 w(t) 图 3.9 响应曲线 2%, 4T s      过渡过程;t 调整时间T ,过渡时间 ，快速性 三、一阶系统的单位斜坡响应   2 11 0 0 1 S 1 1 S S C X S TS              , i x t t    2 1 S S i x 

←2s到现{lL 6日哥里风 T M.=A. C.-[ 1=0,x(=0,e(o)=x(o)-x(o)=T ◆X(0 1/T X()个e(em=T 0.368/T Xo(t)=t-T+TeVr 图3.10响应曲线 瞬态响应的特性反应系统本身的特性，叶响应速度↓。 输入试验信号是为了识别系统的特性，系统特性取决于系统的参数， 不取决于外作用的形式。 例3.2两个T值不同的惯性环节串联，求其单位阶跃响应，已知 G(S)=(S) 11 xS105+1S+7 。11 111_-0.09」 解：xS)-10sS中1s0s+s*1*s 9.1 x0-=0ei+g1

      2 12 2 0 0 0 1 S S 1 S 1 S d d T C X S T ds ds TS   TS                         2 0 2 2 2 1 1 1 T T 1 T T S TS+1 S S S TS+1 S S S+1/T x         M A r  max   2 2 1/ 2 1/ 1 ( s+1) S T S T C X S T T S             t , x t 0    , e x x T ( )       i   0   X0(t) t 1/T 0.368/T e(∞)=T X0(t)=t-T+Te -t/T Xi(t)=t 图 3.10 响应曲线 瞬态响应的特性反应系统本身的特性，T 响应速度 。 输入试验信号是为了识别系统的特性，系统特性取决于系统的参数， 不取决于外作用的形式。 例 3.2 两个 T 值不同的惯性环节串联，求其单位阶跃响应，已知     0 1 1 G(S) 10 1 1 i x S x S S S     = 。 解： x S 0    1 1 1 1 1 1 0.09 9 10 1 1 S 10 1 1 S S S S S           1 L    10 0 1 1 1 0.09 9 t t x t e e      

+Xo(0 w↑S] 2 S2 S1 +0 图3.11响应曲线示意图 图3.12极值分布图 系统响应取决于T,T值小，对响应影响小。 靠近虚轴的极点起主导作用

X0(t) t 3 2 1 jw × × σ s2 s1 [S] 图 3.11 响应曲线示意图 图 3.12 极值分布图 系统响应取决于 T，T 值小，对响应影响小。 靠近虚轴的极点起主导作用

§3.3二阶系统的时域响应 二阶系统：由二阶微分方程描述的系统。 许多高阶系统常近似为二阶系统来研究，所以具有重要意义。 一典型的二阶系统的数学模型 G9=⑨ x(S)S2+250S+m 5:阻尼比0：无阻尼固有频率 令上式分母=0，得二阶系统的特征方程： S2+250S+0,2=0 x=-b生F-4ac 2 极点：S-50,±a,P△=6-4ae(5-43#42 公=2wVg2-) △-2w2(52-1)<0 00<5<1,→欠阻尼S2=-50,±joV- 0=-52→有阻尼固有频率 欠阻尼情况下系统的时间响应具有震荡特性。 系统的响应(2)5=1，→临界阻尼，S2=-50=-0,(一对负实根) 均无振荡【(35>1，→过阻尼，S2=-50.±0V2-1(负实根) v,IS] 51s2 +0 -Wn (b)

§3.3 二阶系统的时域响应 二阶系统：由二阶微分方程描述的系统。 许多高阶系统常近似为二阶系统来研究，所以具有重要意义。 一.典型的二阶系统的数学模型       2 0 2 2 : 2 n n i n n x S G S x S S S          阻尼比 ：无阻尼固有频率 令上式分母 0，得二阶系统的特征方程： 2 2 2 0 n n S S      2 4 2 b b ac x     2 极点：S 1 1 2，        n n   2 2 2 2 2 4 2 4 4 ( 1) n n n        b ac w w w   2 2 ( 1) wn     2 2 2 ( 1) 0     wn  2 1 2 2 (1)0 1, S 1 1 n n d n     j              欠阻尼 ， 有阻尼固有频率 欠阻尼情况下系统的时间响应具有震荡特性。 系统的响应 1 2 (2) 1, S ( )          临界阻尼， ， n n 一对负实根 均无振荡 2 1 2 (3) 1, S 1( )           过阻尼， ， n n 负实根 jw σ × × s2 s1 [S] jwd -jwd -ξwn jw × σ s1 s2 [S] -wn (a) (b)

m↑S) wn不 S2 S1 (c) (d) 图3.13复数域极值分布图 (4)5=0,→零阻尼，S2=±j0,(一对纯虚根) 此时系统的时间响应为持续的等幅振荡。 二阶系统的响应特性完全由5和0，来描述。 二、二阶系统的单位阶跃响应 0=1401-日 x(S)=G(S)5s+25m3+a23 02 1 1当0<5<1，欠阻尼 S2=-50n±j0V-5-50±j0 002 6例-写+2编s+55+a+回js+a-回3 5(() S+50。 50。 M,-25-月 即：x(0=1-e5%cos0,1+ 5

jw × σ s2 s1 [S] × jw σ × s2 s1 [S] wn × (c) (d) 图 3.13 复数域极值分布图 1 2 (4) 0, S ( ) n       零阻尼， ， j 一对纯虚根 此时系统的时间响应为持续的等幅振荡。 二阶系统的响应特性完全由  和 n 来描述。 二、二阶系统的单位阶跃响应         2 0 2 2 1 1, [ ] 1 1 2 i i n n n x t L x t S x S G S S S S S             1. 0 1, 当    欠阻尼 2 S 1 1 2 n n n d ，             j j      2 2 0 2 2 1 1 2 n n n n n d n d x S S S S S j S j S                       2 2 2 2 1 n n n d n d S S S S               2 1 2 1 M r     0   2 1 cos sin 1 n n t t d d x t e t e t                        即：   2 0 2 1 1 sin arctan 1 n t d e x t t                     或：