
(②)实际上是振动相位的传播速度。 t时刻x1处的振动状态经△t时间传播到x,+△x处,则 o(G,-)=oG+△Y-+△ 1 △X 可得到 1= △t (3)若波沿轴负向传播时,同样可得到波函数: yx,t)=4cos[ot+惑+g,】 u (x,)=Acos[2r(1+,)+p] 其 形式 x,0)=Acos2(7++] c,0=Aos牙(w+x)+】
(2) u 实际上是振动相位的传播速度。 t1 时刻x1 处的振动状态经Δt 时间传播到x1+Δx 处,则 ( ) ( ) 1 1 1 1 u x x t t u x t + − = + − 可得到 t x u = (3) 若波沿轴负向传播时,同样可得到波函数: ( , ) cos[ ( ) ] = + +0 u x y x t A t ( ) ] 2π ( , ) cos[ 0 y x t = A ut + x + ( , ) cos[2π ( ) ] 0 = + + x y x t A t ( , ) cos[2π ( ) ] 0 = + + x T t y x t A 其 它 形 式
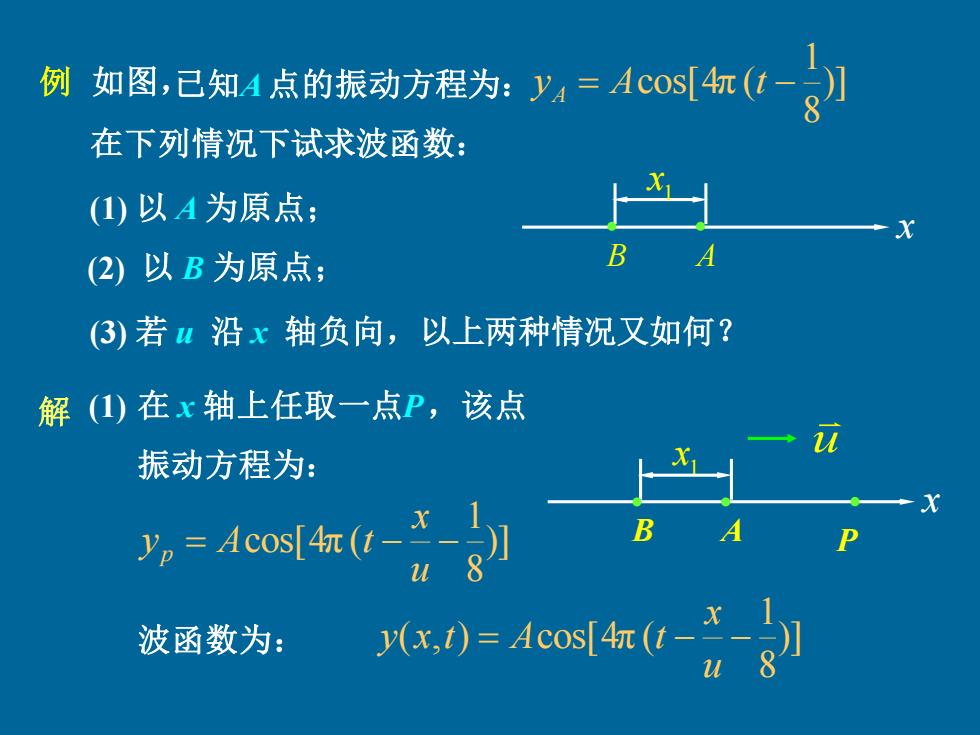
例如图,已知1点的振动方程为:=A00s[红(亿-8】 在下列情况下试求波函数: (1)以A为原点; (2)以B为原点; B A (3)若4沿x轴负向,以上两种情况又如何? 解(1)在x轴上任取一点P,该点 振动方程为: =4do时领0-8 B A P 波函数为: (x,)=Acos[4(t-X-
如图, 在下列情况下试求波函数: )] 8 1 yA = Acos[4π (t − (3) 若 u 沿 x 轴负向,以上两种情况又如何? 例 (1) 以 A 为原点; (2) 以 B 为原点; B A 1 x x 已知A 点的振动方程为: u (1) 在 x 轴上任取一点P ,该点 振动方程为: )] 8 1 = cos[4π ( − − u x y A t p )] 8 1 ( , ) = cos[4π ( − − u x 波函数为: y x t A t 解 P 1 x B A x

②B点振动方程为:%0=4c0s[红化+开-发】 波函数为: y(x,t)=Acos[4 (t u 3)以A为原点: y(x.t)=Acos[4 (t+x) 2u8 以B为原点: )Acos 1-】
(2) B 点振动方程为: )] 8 1 ( ) cos[4π ( 1 = + − u x y t A t B )] 8 1 ( , ) cos[4π ( 1 − − = + u x x y x t A t )] 8 1 ( , ) = cos[4π ( + − u x (3) 以 A 为原点: y x t A t 以 B 为原点: 波函数为: )] 8 1 ( , ) cos[4π ( 1 − − = − u x x y x t A t

二,波函数的物理意义 (1)振动状态的空间周期性 y(x+入,t)=V(x,t),说明波线上振动状态的空间周期性 (2)波形传播的时间周期性 V(x,t+T)=y(x,t),说明波形传播的时间周期性 ③)x给定,y=y(0)是x处振动方程 (④)t给定,y=心)表示t时刻的波形图 (⑤)y给定,x和t都 t汁时刻的波形 t,时刻的波形 在变化,表明波 形传播和分布的 时空周期性
二. 波函数的物理意义 (2) 波形传播的时间周期性 (1) 振动状态的空间周期性 y(x + ,t) = y(x,t), 说明波线上振动状态的空间周期性 y(x,t +T) = y(x,t), 说明波形传播的时间周期性 t1时刻的波形 O y x u x1 + x (4) t 给定,y = y(x) 表示 t 时刻的波形图 (5) y 给定, x和 t 都 在变化,表明波 形传播和分布的 时空周期性。 (3) x 给定,y = y (t) 是 x 处振动方程 t1+Δt时刻的波形 x1

例一平面简谐波沿x轴正方向传播,已知其波函数为 y=0.04cosπ(50t-0.10x)m 求()波的振幅、波长、周期及波速; (②)质点振动的最大速度。 解(1)a.比较法(与标准形式比较) 标准形式 x)=Acos2x(7-为+,】 500.10 波函数为 y=0.04cos2x(27- x) 2 2 比较可得 A=0.04m T= 0.04S 50 人、2 =20m =500m/s 0.10
一平面简谐波沿x轴正方向传播,已知其波函数为 y = 0.04cos (50t − 0.10x) m ) 2 0.10 2 50 y = 0.04cos 2π ( t − x A = 0.04 m 0.04 s 50 2 T = = 20 m 0.10 2 = = = = 500 m/s T u a. 比较法(与标准形式比较) ( , ) cos[2π ( ) ] 0 = − + x T t 标准形式 y x t A 波函数为 比较可得 例 解 (1) 波的振幅、波长、周期及波速; (2) 质点振动的最大速度。 求 (1)