
相位差 ÷两个同频率正弦波的初相角的差值反映了它们“步 调”不一致的情况。初相角之差称为相位差角,简 称为相位差。以p12表示u与u2的相位差,即 p12=(ot+9)-(ot+02)=01-02 p12代表u1的相位超前于u2或u2的相位滞后于w1的角度。 般要求p12l≤π :i 11
相位差 ❖ 两个同频率正弦波的初相角的差值反映了它们“步 调”不一致的情况。初相角之差称为相位差角,简 称为相位差。以12表示ul与u2的相位差,即 11 ( ) ( ) 12 = +1 − + 2 =1 − 2 t t ❖12代表u1的相位超前于u2或u2的相位滞后于u1的角度。 一般要求 |12|
相位差的特例 ?如果相位差为零,则两个正弦波同相位,简称同相。 冬如果相位差为士π2,则两个正弦波为相位正交。 如果相位差为π,则两个正弦波为反相位,简称反相。 (a) (c) (b) 12
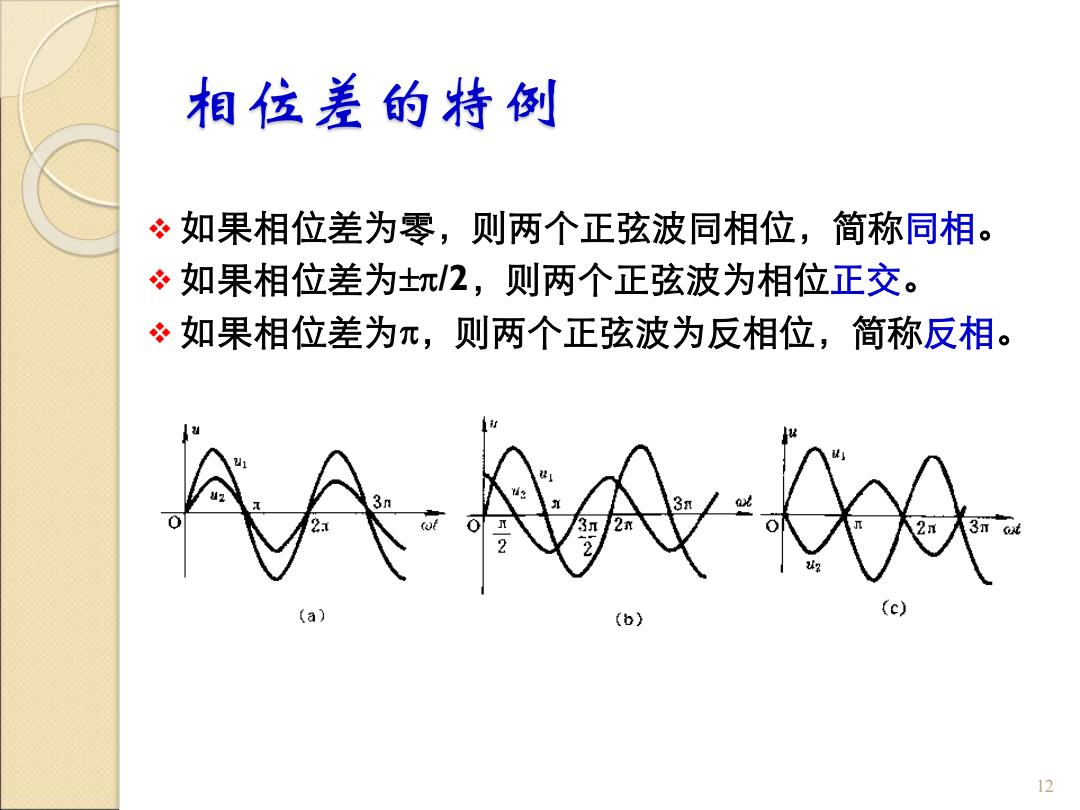
相位差的特例 ❖ 如果相位差为零,则两个正弦波同相位,简称同相。 ❖ 如果相位差为/2,则两个正弦波为相位正交。 ❖ 如果相位差为,则两个正弦波为反相位,简称反相。 12
§.3正孩RC电路的分析 求解RC电路在正弦电流作用 下的响应uc(t)。 设输入到RC电路的正弦电流为 (a} i,(t)=Ism cos(@t+0)t> 电路的微分方程 ,de+bc=1coo+0) t≥0 (b) dt R 4c(0)=0 uo Ke Rc' 通解 为了确定Ucm和,两个常 ucp =Ucm cos(@t+e,) 特解 数,可将特解代入方程 13
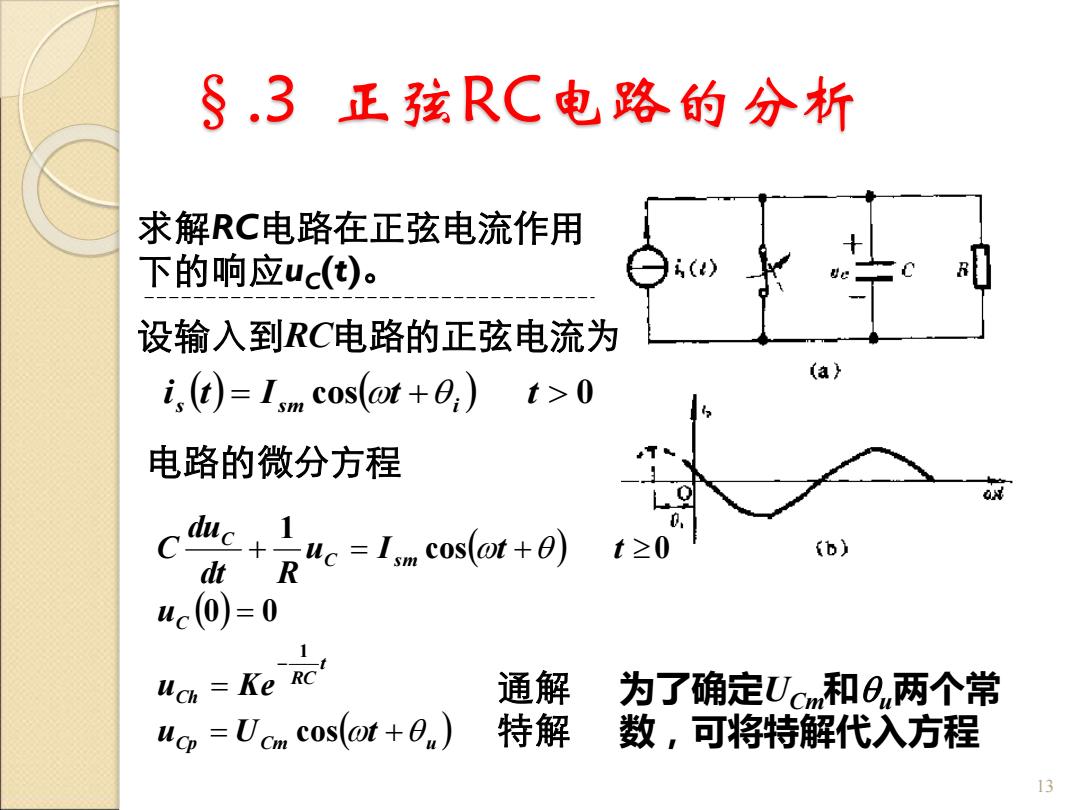
§.3 正弦RC电路的分析 求解RC电路在正弦电流作用 下的响应uC(t)。 13 设输入到RC电路的正弦电流为 i s (t) = Ism cos(t + i ) t 0 电路的微分方程 ( ) ( ) ( ) Cp Cm u t RC Ch C C s m C u U t u Ke u u I t t dt R du C = + = = + = + − cos 0 0 cos 0 1 1 通解 特解 为了确定UCm和 u两个常 数,可将特解代入方程

微分方程的完全解 由于正弦函数的导数仍为同频率的正弦函数,可得 -Csin(a+g))-oo+,)=L.oslt+0 c2oc,go+2+i2aR=nonla+】 oc2+ 0=0+ArctgoCR →0.=0:-Arctg@CR uc(t)=Ke RC'+Ucn cos(@t+0) 14
微分方程的完全解 ❖ 由于正弦函数的导数仍为同频率的正弦函数,可得 14 ( ) ( ) ( ) ( ) ( ) Arctg C R Arctg C R R C I U R U I U C t Arctg C R I t R U U C t I t R U C U t i u u i s m Cm Cm s m Cm u s m i Cm Cm u s m i Cm Cm u = + = − + = + = + + + = + − + + + = + 2 2 2 2 2 2 2 2 2 2 2 2 2 1 cos cos sin cos cos ( ) ( ) Cm u t RC C u t = Ke +U t + − cos 1
求解K K可根据初始条件uc(O)求得 uc(0)=K+Ucm cos(0.) K=uc(0)-Uc cos(e)=-Ucn cos(e) 零状态响应为 稳态响应 ue()--Von sos(0,e cos0) t≥0 暂态响应 H(t】 15
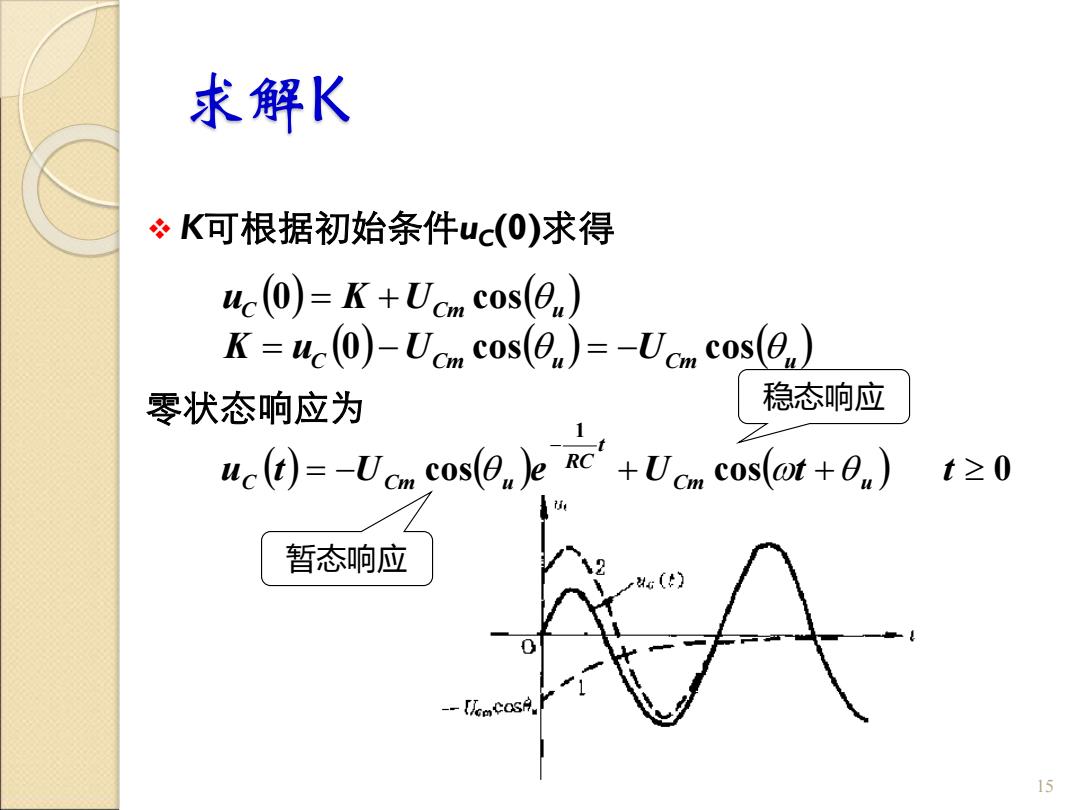
求解K ❖ K可根据初始条件uC(0)求得 15 ( ) ( ) ( ) ( ) ( ) C Cm u Cm u C Cm u K u U U u K U 0 cos cos 0 cos = − = − = + ( ) cos( ) cos( ) 0 1 = − + + − u t U e U t t Cm u t RC C Cm u 零状态响应为 暂态响应 稳态响应