
第二章射频设计中的主要参量与接收机架构 线性度,可以将增益尽量加在后级。这个原则作为我们之后为TV-tuner芯片的 各模块如何分配增益提供了一个理论依据。 2.1.3宽带信号的三阶交调 在以上的讨论中,我们考虑的都是单频点或者两个频点的情况,但是在实际 应该中,信号的传输一般都是在一段频率内,而不是一个频点,在众多传输标准 中,一个频道的带宽也各不相同,比如美国的ATSC标准中一个频道的带宽为6 M,日本的SDB-T标准中一个频道的带宽可以从430k到8M不等。因此使用 单频点来分析信号传输明显存在很多问题,相对于单频点,宽带信号的三阶交调 就十分有必要进行详细的研究[6]。 宽带信号的各个频点处产生的交调量是由众多频率上的信号交调量之和,为 了计算整个带宽内的交调量,我们假设信号在整个频道内具有平坦的频谱,频道 带宽为B。根据式(2.9),我们可以把三阶交调量转换到功率表示出来, PxG P (2.17) G表示系统的一阶功率增益。P为整个频道内一个单频点的输入功率, 那么整 个频道的输入功率为, Pin.total Pin x B (2.18) 这里,我们可以把这个三阶交调量等效到输入端,可以得到, (2.19) P B1 wx Wa1 WB1 B1 Wa2 WB2 Wx B2 (a) (b) 图2-5一个频点三阶交调量的两种产生方式 对于一个频率为wx的三阶交调点,产生它的双声(two-tone)信号有两种可能 性,第一种是大于wx的两个频率:wa1=wx+W和WB1=wk+2W△,则2wa1一 wB1=wk,如图2-5(a)所示。第二种是小于wx的两个频率:wa2=wk-2w和 wB2=W-WA,则2wB2-wa2=wx,如图2-5(b)所示。假设这个频道的频率上 下限分别为B1和B2,易知B2-B1=B,我们可以对每一种情况进行积分,然
第二章 射频设计中的主要参量与接收机架构 8 线性度,可以将增益尽量加在后级。这个原则作为我们之后为 TV-tuner 芯片的 各模块如何分配增益提供了一个理论依据。 2.1.3 宽带信号的三阶交调 在以上的讨论中,我们考虑的都是单频点或者两个频点的情况,但是在实际 应该中,信号的传输一般都是在一段频率内,而不是一个频点,在众多传输标准 中,一个频道的带宽也各不相同,比如美国的 ATSC 标准中一个频道的带宽为 6 M,日本的 ISDB-T 标准中一个频道的带宽可以从 430 k 到 8 M 不等。因此使用 单频点来分析信号传输明显存在很多问题,相对于单频点,宽带信号的三阶交调 就十分有必要进行详细的研究[6]。 宽带信号的各个频点处产生的交调量是由众多频率上的信号交调量之和,为 了计算整个带宽内的交调量,我们假设信号在整个频道内具有平坦的频谱,频道 带宽为 B。根据式(2.9),我们可以把三阶交调量转换到功率表示出来, 3 in OIM3 2 IIP3 P G P P (2.17) G 表示系统的一阶功率增益。Pin 为整个频道内一个单频点的输入功率,那么整 个频道的输入功率为, P PB in,total in (2.18) 这里,我们可以把这个三阶交调量等效到输入端,可以得到, 3 in IIM3 2 IIP3 P P P (2.19) (a) (b) 图 2-5 一个频点三阶交调量的两种产生方式 对于一个频率为 ωx的三阶交调点,产生它的双声(two-tone)信号有两种可能 性,第一种是大于 ωx 的两个频率:ωα1 = ωx + ω∆ 和 ωβ1 = ωx + 2ω∆,则 2ωα1 – ωβ1 = ωx,如图 2-5 (a)所示。第二种是小于 ωx的两个频率:ωα2 = ωx – 2ω∆和 ωβ2 = ωx – ω∆,则 2ωβ2 – ωα2 = ωx,如图 2-5(b)所示。假设这个频道的频率上 下限分别为 B1 和 B2,易知 B2 – B1 = B,我们可以对每一种情况进行积分,然

第二章射频设计中的主要参量与接收机架构 后将两种情况积分所得的三阶交调量加在一起,就可以得到某一个频点的总的三 阶交调量。 对于第一种情况,我们对w积分,易知,wa的边界条件为0<w<0.5X(B2 -w),那么根据式(2.19)可以得到等效到输入的M3,1, B2 Pdw 2 (2.20) P2 IIP3 整理化简可得, PM3,1= B2-W 2 P (2.21) 对于第二种情况,我们对w积分,易知,wa的边界条件为0<w<0.5x(w -B1),那么根据式(2.19)可以得到等效到输入的M3,2, wX-B1 P3 P32= 2 in dw (2.22) Jo 整理化简可得, Pi.=,B1 P 2xp2 (2.23) 1P3 将两种情况下的三阶交调量求和,就得到位于ω处的等效到输入的总三阶交调 量, Ps=Pa1+PMa2=( B2-Wx w,-B1 PBx P 2 2 (2.24) P品2P 由于频道带宽为B,那么可以求得整个频道的等效输入三阶交调量, Psa=R×B=S×BP_Pa (2.25) P3×2BP×2B 从式(2.25)可以知道,当输入功率不变时,总的等效输入三阶交调量与频道带宽 成反比。 2.1.4复合三阶失真 以上对宽带三阶交调量的讨论都是基于两个频点交调得到的,但是在实际的 宽频中,三个频点在一起混频也可以产生与三个频率相关的三阶交调量,我们将 这种交调量称为复合三阶交调,由这种交调量产生的失真称为复合三阶失真。 为了更好的说明复合三阶失真,我们取宽带内的三个频点w1、w2、w3,则 输入信号可以表示为X(⑤=AC0Sω1t+Ac0SwW2t+AC0Sω3t,那么,输出可以表示 为
第二章 射频设计中的主要参量与接收机架构 9 后将两种情况积分所得的三阶交调量加在一起,就可以得到某一个频点的总的三 阶交调量。 对于第一种情况,我们对 ω∆积分,易知,ω∆的边界条件为 0 < ω∆ < 0.5 x (B2 – ωx),那么根据式(2.19)可以得到等效到输入的 IIM3,1, 2 x 3 2 in IIM3,1 2 0 IIP3 d B ω P P ω P (2.20) 整理化简可得, 3 x in IIM3,1 2 IIP3 2 2 B ω P P P (2.21) 对于第二种情况,我们对 ω∆积分,易知,ω∆的边界条件为 0 < ω∆ < 0.5 x (ωx – B1),那么根据式(2.19)可以得到等效到输入的 IIM3,2, x 1 3 2 in IIM3,2 2 0 IIP3 d ω B P P ω P (2.22) 整理化简可得, 3 x in IIM3,1 2 IIP3 1 2 ω B P P P (2.23) 将两种情况下的三阶交调量求和,就得到位于 ωx处的等效到输入的总三阶交调 量, 3 3 x x in in IIM3 IIM3,1 IIM3,2 2 2 IIP3 IIP3 2 1 ( ) 22 2 B ω ω BP P B PP P P P (2.24) 由于频道带宽为 B,那么可以求得整个频道的等效输入三阶交调量, 3 3 in,total in IIM3,total IIM3 2 2 IIP3 IIP3 ( ) 2 2 P B P P PB P BP B (2.25) 从式(2.25)可以知道,当输入功率不变时,总的等效输入三阶交调量与频道带宽 成反比。 2.1.4 复合三阶失真 以上对宽带三阶交调量的讨论都是基于两个频点交调得到的,但是在实际的 宽频中,三个频点在一起混频也可以产生与三个频率相关的三阶交调量,我们将 这种交调量称为复合三阶交调,由这种交调量产生的失真称为复合三阶失真。 为了更好的说明复合三阶失真,我们取宽带内的三个频点 ω1、ω2、ω3,则 输入信号可以表示为 x(t) = Acosω1t + Acosω2t + Acosω3t,那么,输出可以表示 为
第二章射频设计中的主要参量与接收机架构 y(t)=a,(Ac0sω,t+Ac0sW2t+Ac0sw3t) +a2(Ac0Sw,t+Acosw,t+Acosω,t)2 (2.26) +a3(Ac0sw,t+Acosw2t+Acosω,t)3 由于我们关注的是三个频点的复合交调,因此我们只展开三阶项,可以得到, 3 y()-d,A[Cos(@,+w.+w.)t+cos(w,+w,-w,) (2.27) +C0s(w,-w2+w3)t+C0s(w1-w2-w3)t1]+… 其中位于ω1+w2+处的交调量一般会因为频率较高而落于带外,那么比较 重要的产生复合三阶交调量的频率是w1+w2-w3、w1-w2+w3、w2+w3-W1, 与两个频率互交调产生的三阶量相比,参考式(2.5),复合三阶交调量在幅度上是 互交调量的2倍,那么反应到功率上,复合三阶交调量是互交调量的4倍,根 据式(2.19),可以得到等效到输入的复合三阶交调量, PM=4 P (2.28) FlIP3 这里的Pn为整个频道内一个单频点的输入功率。 A+B A-B 2A+B 24B A+B+C A-B+C A+B-C AB-C CARRIER FREQUENCIES 1500 .1000 -500 0 500 10001500 2000 2500 FREQUENCY 图2-6互交调与复合三阶交调产生差拍数对比 为了计算一个频点上所有的复合三阶交调量,我们需要知道在整个频带上的 10
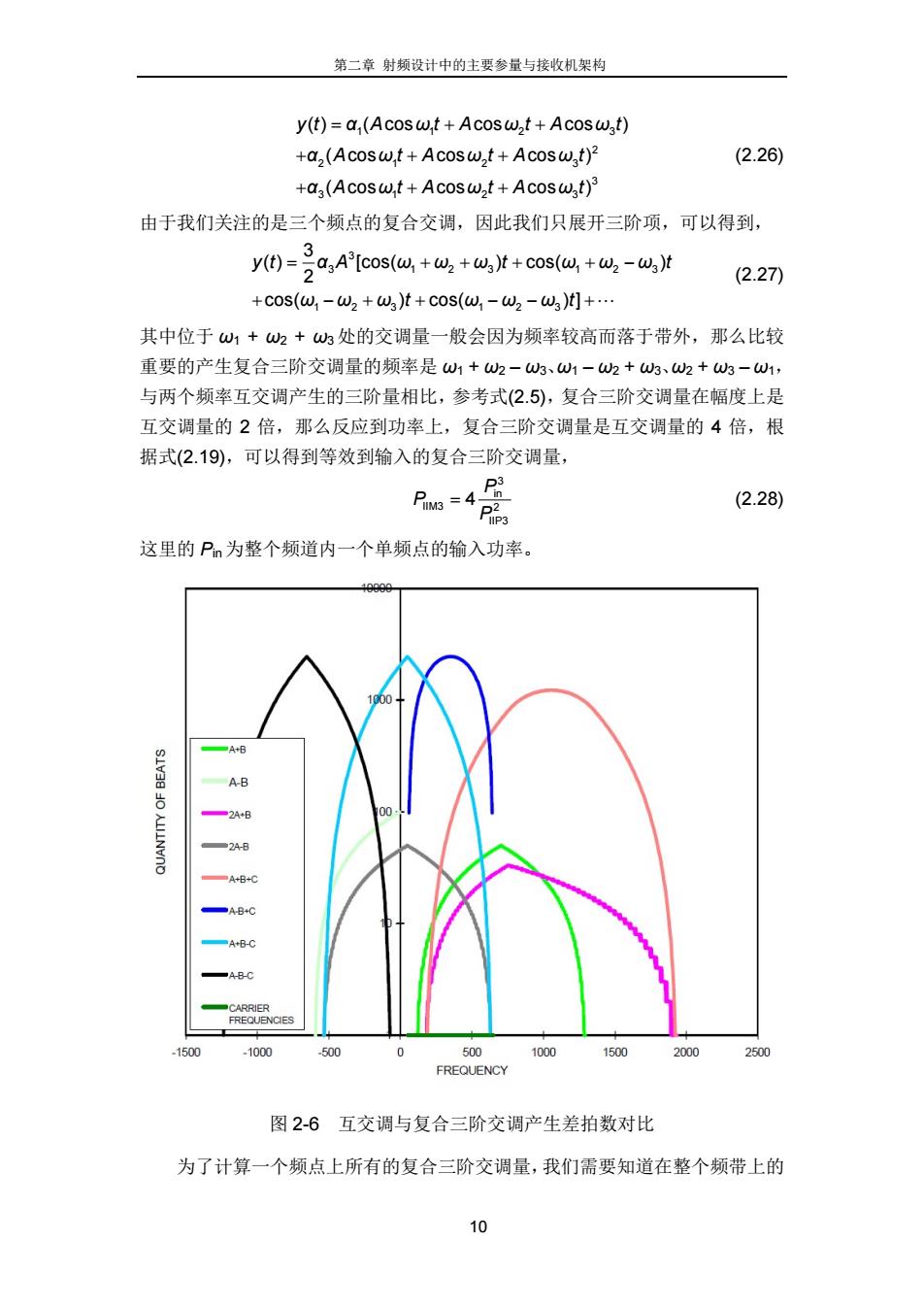
第二章 射频设计中的主要参量与接收机架构 10 11 2 3 2 21 2 3 3 31 2 3 ( ) ( cos cos cos ) ( cos cos cos ) ( cos cos cos ) y t α A ω t A ω t A ω t α A ω t A ω t A ω t α A ω t A ω t A ω t (2.26) 由于我们关注的是三个频点的复合交调,因此我们只展开三阶项,可以得到, 3 3 123 123 12 3 123 3 ( ) [cos( ) cos( ) 2 cos( ) cos( ) ] y t α A ωωω t ωωω t ωω ω t ωωω t (2.27) 其中位于 ω1 + ω2 + ω3处的交调量一般会因为频率较高而落于带外,那么比较 重要的产生复合三阶交调量的频率是 ω1 + ω2 – ω3、ω1 – ω2 + ω3、ω2 + ω3 – ω1, 与两个频率互交调产生的三阶量相比,参考式(2.5),复合三阶交调量在幅度上是 互交调量的 2 倍,那么反应到功率上,复合三阶交调量是互交调量的 4 倍,根 据式(2.19),可以得到等效到输入的复合三阶交调量, 3 in IIM3 2 IIP3 4 P P P (2.28) 这里的 Pin为整个频道内一个单频点的输入功率。 图 2-6 互交调与复合三阶交调产生差拍数对比 为了计算一个频点上所有的复合三阶交调量,我们需要知道在整个频带上的

第二章射频设计中的主要参量与接收机架构 信号在某一频点上所产生的交调量数量,这里通常称为复合三阶差拍 (Composite Triple Beats,CTBs)。如果将两个频率的互交调在某一频点上产生的 交调量数量也用差拍数表示,复合三阶差拍数要远远大于互交调差拍数,如图 2-6所示[7]。其中的A、B、C表示w1、w2、w3三个频率处的信号,并且假设 ω1<w2<W30 因此,无论从单个交调量的大小来说,还是从交调量的差拍数来讲,复合三 阶交调量都要远远超过互交调量从而成为影响信号线性度的主要因素,因此有必 要对复合三阶交调量进行具体的计算,图27显示了在宽带内复合三阶差拍的 分布7]。 Sum of Beats wn+W2-W3 Quantity of Beats Wh一w2+3 Wk+W3-W1 B1 B2 Frequency 图2-7宽带信号的复合三阶差拍分布 从图27中可以看到,位于频带中心位置的频点上复合三阶差拍数最多,如 果我们将带宽B量化为N个频点,那么第M个频点上的三阶差拍数为T], beats= N2,(N-M(M-1) (2.29) 4 2 当M=N/2时, beats≈3W2 (2.30) 相近的结果可以在另外一篇文献中找到[8],第M个频点上的复合三阶差拍 数的公式为, beats=(M+N):-3M2+2M-6N+3 (2.31) 当M=N/2时, 11
第二章 射频设计中的主要参量与接收机架构 11 信号在某一频点上所产生的交调量数量,这里通常称为复合三阶差拍 (Composite Triple Beats, CTBs)。如果将两个频率的互交调在某一频点上产生的 交调量数量也用差拍数表示,复合三阶差拍数要远远大于互交调差拍数,如图 2-6 所示[7]。其中的 A、B、C 表示 ω1、ω2、ω3 三个频率处的信号,并且假设 ω1 < ω2 < ω3。 因此,无论从单个交调量的大小来说,还是从交调量的差拍数来讲,复合三 阶交调量都要远远超过互交调量从而成为影响信号线性度的主要因素,因此有必 要对复合三阶交调量进行具体的计算, 图 2-7 显示了在宽带内复合三阶差拍的 分布[7]。 图 2-7 宽带信号的复合三阶差拍分布 从图 2-7 中可以看到,位于频带中心位置的频点上复合三阶差拍数最多,如 果我们将带宽 B 量化为 N 个频点,那么第 M 个频点上的三阶差拍数为[7], 2 ( )( 1) beats 4 2 N N MM (2.29) 当 M = N/2 时, 2 3 beats 8 N (2.30) 相近的结果可以在另外一篇文献中找到[8],第 M 个频点上的复合三阶差拍 数的公式为, 2 2 ( )3 2 6 3 beats 4 MN M M N (2.31) 当 M = N/2 时

第二章射频设计中的主要参量与接收机架构 beats=3N2-10N+6 (2.32) 8 当N趋于无穷大时,式(2.30)和式(2.32)所表示的差拍数都可以简化为式 (2.30),关于复合三阶差拍数的公式,并没有比较统一的形式,但是各类文献所 推导出来的公式差别不是很大,主要都是参考了测试结果,具体内容可以参考文 献[7[8]. 根据式(2.30)和式(2.28),可以得到中心频点处等效到输入的总复合三阶交 调量, PeT4P3N3NP (2.33) Plip3 8 2PiP3 P2 那么,考虑非线性最恶化的情况,我们令整个频道内的复合三阶交调量都与式 (2.33)相同,则整个频道的复合三阶交调量为, P PeToNPN)33P in,total (2.34) P 22P 2.2噪声 噪声在电路中是一个与信号源无关的随机电信号,噪声的存在限制了系统能 够正确处理的输入信号最小值,因为太小的信号会湮没于噪底中,因此,同非线 性的研究目的相类似,噪声的研究对系统的功耗,速度等性能都有着十分重要的 意义。 2.2.1信噪比 信噪比(Signal to Noise Ratio,.SNR)定义为信号功率与总噪声功率的比值。 对于一个二端口网络,由于信号跟噪声有输入端跟输出端之分,因此信噪比也分 为输入信噪比和输出信噪比, SNRn= Psignal.in (2.35) SNRout= 尸ilou 为了计算信噪比,我们假设一个低噪声放大器(LNA)通过天线接入一个射频 信号,如图2-8所示。如果低噪声放大器的输入阻抗为Z,那么可以求得输入 SNR和输出SNR, 12
第二章 射频设计中的主要参量与接收机架构 12 2 3 10 6 beats 8 N N (2.32) 当 N 趋于无穷大时,式(2.30)和式(2.32)所表示的差拍数都可以简化为式 (2.30),关于复合三阶差拍数的公式,并没有比较统一的形式,但是各类文献所 推导出来的公式差别不是很大,主要都是参考了测试结果,具体内容可以参考文 献[7][8]。 根据式(2.30)和式(2.28),可以得到中心频点处等效到输入的总复合三阶交 调量, 3 23 2 in in CTB,single 2 2 IIP3 IIP3 3 3 4 8 2 P NP N P P P (2.33) 那么,考虑非线性最恶化的情况,我们令整个频道内的复合三阶交调量都与式 (2.33)相同,则整个频道的复合三阶交调量为, 3 3 in,total in CTB,total CTB,single 2 2 IIP3 IIP3 ( ) 3 3 2 2 P N P PP N P P (2.34) 2.2 噪声 噪声在电路中是一个与信号源无关的随机电信号,噪声的存在限制了系统能 够正确处理的输入信号最小值,因为太小的信号会湮没于噪底中,因此,同非线 性的研究目的相类似,噪声的研究对系统的功耗,速度等性能都有着十分重要的 意义。 2.2.1 信噪比 信噪比(Signal to Noise Ratio, SNR)定义为信号功率与总噪声功率的比值。 对于一个二端口网络,由于信号跟噪声有输入端跟输出端之分,因此信噪比也分 为输入信噪比和输出信噪比, signal,in in noise,in signal,out out noise,out P SNR P P SNR P (2.35) 为了计算信噪比,我们假设一个低噪声放大器(LNA)通过天线接入一个射频 信号,如图 2-8 所示。如果低噪声放大器的输入阻抗为 Zin,那么可以求得输入 SNR 和输出 SNR