3、用试验方法求取 首先,改变输入谐波信号Xiejwt的频率ω,并测出 与相应的输出幅值Xo(ω)与相位φ(ω)。然后,做出幅 值比Xo(⊙X对频率ω的函数曲线,即幅频特性曲线; 作出相位φ(ω)对频率ω的函数曲线,即相频特性曲线。 d微分方程d dt dt 系统 传递函数 频率特性 S jw
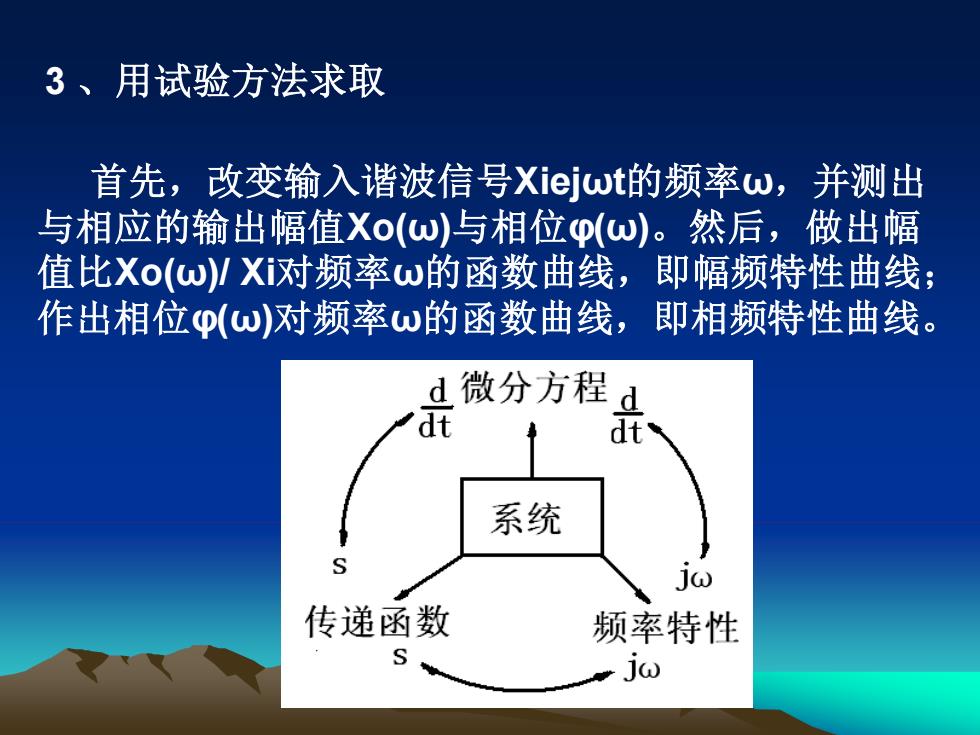
3 、用试验方法求取 首先,改变输入谐波信号Xiejωt的频率ω,并测出 与相应的输出幅值Xo(ω)与相位φ(ω)。然后,做出幅 值比Xo(ω)/ Xi对频率ω的函数曲线,即幅频特性曲线; 作出相位φ(ω)对频率ω的函数曲线,即相频特性曲线

四、频率特性的特点和作用 (1) 由Xo(s)=G(s)Xis有 Xo(jo)=G(jo)xi(jo) 而当xi①)=δ()时,xo()=w(): 且XiGo)=F[δ(t)=1 故Xo(Gjo=GGo) F[w(t)]=G(j@) 这表明系统的频率特性就是单位脉冲响应函数 w(①的Fourierz变换,即w(t)的频谱
四、频率特性的特点和作用 (1) 由Xo(s)=G(s)Xi(s)有 Xo(jω)=G(jω)Xi(jω) 而当 xi(t)=δ(t)时,xo(t)=w(t), 且 Xi(jω)=F[δ(t)]=1 故 Xo(jω)=G(jω) F[w(t)]=G(jω) 这表明系统的频率特性就是单位脉冲响应函数 w(t)的Fourier变换,即w(t)的频谱

(2)时间响应分析主要分析线性系统过渡过程, 获取系统的动态特性;而频率特性分析不同的谐波 输入时系统的稳态响应,获取系统的动态特性。 (3)在研究系统的结构及参数的变化对系统性能 的影响时,许多情况,在频域中分析要容易得多。 特别是频率特性可方便地判别系统的稳定性和稳定 储备量,参数选择或系统校正,使系统尽可能达到 预期的性能指标。根据频率特性,易于确定系统频 率范围
(2) 时间响应分析主要分析线性系统过渡过程, 获取系统的动态特性;而频率特性分析不同的谐波 输入时系统的稳态响应,获取系统的动态特性。 (3) 在研究系统的结构及参数的变化对系统性能 的影响时,许多情况,在频域中分析要容易得多。 特别是频率特性可方便地判别系统的稳定性和稳定 储备量,参数选择或系统校正,使系统尽可能达到 预期的性能指标。根据频率特性,易于确定系统频 率范围

(4)若线性系统的阶次较高,特别是对于不 能用分析法得出微分方程的系统,在时域中分 析系统的性能很困难,采用频率特性分析就很 容易。 (5)系统在输入信号的同时,在某些频带中 有着严重的噪声干扰,则对系统采用频率特性 分析法可设计出合适的通频带,以抑制噪声的 影响
(4)若线性系统的阶次较高,特别是对于不 能用分析法得出微分方程的系统,在时域中分 析系统的性能很困难,采用频率特性分析就很 容易。 (5)系统在输入信号的同时,在某些频带中 有着严重的噪声干扰,则对系统采用频率特性 分析法可设计出合适的通频带,以抑制噪声的 影响

§4.2频率特性的图示方法 一、 频率特性 的极坐标图 Im G[(jw)] 1、典型环节 的Nyquist图 (1)比例环节 K G(jo=K 0 Re G(jo)=K ∠G(Uw)=0°
§4.2 频率特性的图示方法 一、频率特 性 的极坐标图 1 、典型环节 的Nyquist图 (1)比例环节 = = = ( ) 0 ( ) ( ) G j G j K G j K 0 Re Im G[(jω)] K