
系统的输出 X。(s)=G(s)X,(s)= bns+bm-s-1++bs+b2。X,0 ans”+an-s-+.+a4+a。s2+ 2 若系统无重极点 X)=2 B ,B s-S s-jo s+ja x(1)=>A,e+(Belo+B*e-jo) i=1 稳态响应为 x(t)=Bejo+B*e-jor
系统的输出 2 2 1 1 1 1 1 1 ( ) ( ) ( ) + • + + + + + + + + = = − − − − s X a s a s a s a b s b s b s b X s G s X s i o n n n n o m m m m o i 若系统无重极点 ( ) ( ) * 1 s j B s j B s s A X s n i i i o + + − + − = = ( ) ( * ) 1 j t j t n i s t o i x t A e Be B e i − = = + + 稳态响应为 j t j t o x t Be B e − ( ) = + *

若系统含有k重极点,则输出含 te(U=1,2,.k-1) 对于稳定系统,由于s的实部为负, 的增长没有 e 的衰减快。所以te 随着t→o0 也趋于零。 X,⊙ B-G(5)(s-joXs+j0) s-j0) =G(S) X,0 s=jo (s+j0)s=j0 Go.-G(jpm. 2j X -2j ,()=G(jo)X elo+GUo-eo+ZG(jo) 则稳态响应为 2j =G(j@)X;sin[@t+ZG(j@)]
若系统含有k重极点,则输出含 t e ( j = 1,2, k −1) k s t j 对于稳定系统,由于sj的实部为负, k t 的增长没有 s t j e 的衰减快。所以 k s t j t e 随着 t → 也趋于零。 j X G j e j X G j s j X s j G s s j s j X B G s i j G j i s j i s j i 2 ( ) 2 ( ) ( ) ( ) ( ) ( )( ) ( ) ( ) = • = • + − = − + = = = j X G j e j X B G j i j G j i 2 ( ) 2 * ( ) ( ) − = • − = − • − 则稳态响应为 ( ) sin[ ( )] 2 ( ) ( ) [ ( )] [ ( )] G j X t G j j e e x t G j X i j t G j j t G j o i = + − = + − +

系统的幅频和相频特性分别为 A(0)= Xo(0) =G(jo川 Xi p(o)=∠G(jo) 故 G(jo)G(Ujo)川eGUo) 就是系统的频率特性。量纲同传递函数。 由于Gω)是一个复变函数,可以写成实部和虚部之和, 即 G(j@)=Re[G(j@)]+Im[G(j@)]=u(@)+jv@) 实频特性 v(@) 虚频特性
系统的幅频和相频特性分别为 = = = ( ) ( ) | ( ) | ( ) ( ) G j G j Xi Xo A 故 ( ) ( ) | ( ) | j G j G j G j e = 就是系统的频率特性。量纲同传递函数。 由于G(jω)是一个复变函数,可以写成实部和虚部之和, 即 G(j) = Re[G(j)]+ Im[G(j)] = u() + jv() u() 实频特性 v() 虚频特性
三、频率特性的求法 1、根据系统的频率响应来求取 X,0 X,(s)= s2+02 xo(t)=L[G(s) X,0 从稳态响应中可得到频率响应的幅值和相位。 例 x(t)= XK sin(ot -arctan To) V1+T2o K A(0)= X.(@) (@)=-arctan To X V1+T2@
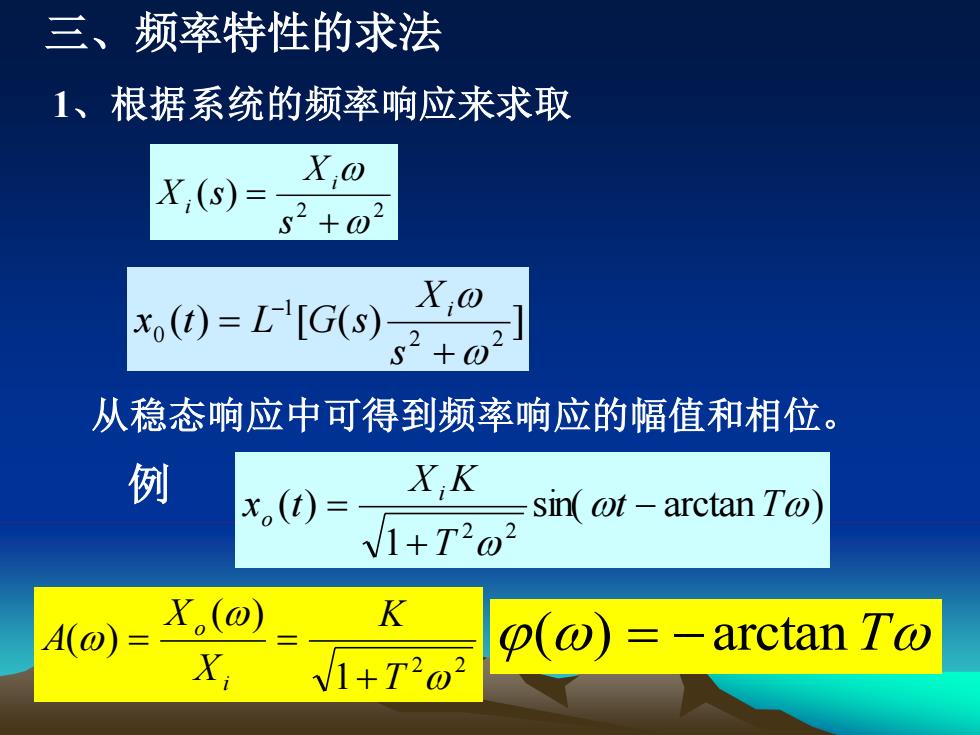
三、频率特性的求法 1、根据系统的频率响应来求取 2 2 ( ) + = s X X s i i ( ) [ ( ) ] 2 2 1 0 + = − s X x t L G s i 从稳态响应中可得到频率响应的幅值和相位。 sin( arctan ) 1 ( ) 2 2 t T T X K x t i o − + 例 = 2 2 1 ( ) ( ) T K X X A i o + = = () = −arctan T

2、将传递函数中的s换为jω(sj)来求取 将系统的传递函数G(s)中的s换为j四, 即为系统的频率特性。 G(j@)=G(s)s-J0 K K ejarctanTo 1+iTo v1+T2@2 K A()= X.(@) p(⊙) =-arctan To X V1+T202 x (t)=X G(s)sin[@t+G(s)] X,K sin(ot-arctan To) v1+T2@
2、 将传递函数中的s 换为jω(s=jω)来求取 将系统的传递函数G(s)中的s换为jω, 即为系统的频率特性。 j T s j e T K j T K G j G s arctan 2 2 1 1 ( ) ( ) − = + = + = = 2 2 1 ( ) ( ) T K X X A i o + = = () = −arctan T sin( arctan ) 1 ( ) ( ) sin[ ( )] 2 2 t T T X K x t X G s t G s i o i − + = = +