
讨论:△t推动力q=1.可表示为R热阻b△t =(ti -t2)推动力:热阻:R=元2.分析平壁内的温度分布Adtqdx = -l上限由x=b时,t=t2为x=x时,t=tqx因为t=tg=-(ti-t2)25x故平壁内任一等温面的温度为b
讨论: 热阻 推动力 = Δ = R t q Δttt = ( ) 1 2 − λ b R = 2.分析平壁内的温度分布 ∫∫ −= 2 0 1 q tt b λdtdx 上限由 2 = 时, = ttbx xx tt = = 时, λ λ x tttt x q 1 )(q 1−=⇒−= 1.可表示为 推动力: 热阻: 为 x b tt tt 21 1 − 故平壁内任一等温面的温度为 −= )( 21 tt b q −= λ 因为

2不随t变化(常数),t~x成呈线形关系。α= k。+kT若随变化关系为:则t~x呈抛物线关系。3.当a随变化时=( +) /2如:,热导率可取两壁面温度下入值的算术平均值
λ不随t变化(常数), t~x成呈线形关系。 3.当λ随t变化时 λ = ( )/ λ1 2 + λ 2 若λ随t变化关系为: 则t~x呈抛物线关系。 如:λ1~t1,λ2~t2 = + kTk λ 0 热导率可取两壁面温度下λ值的算术平均值
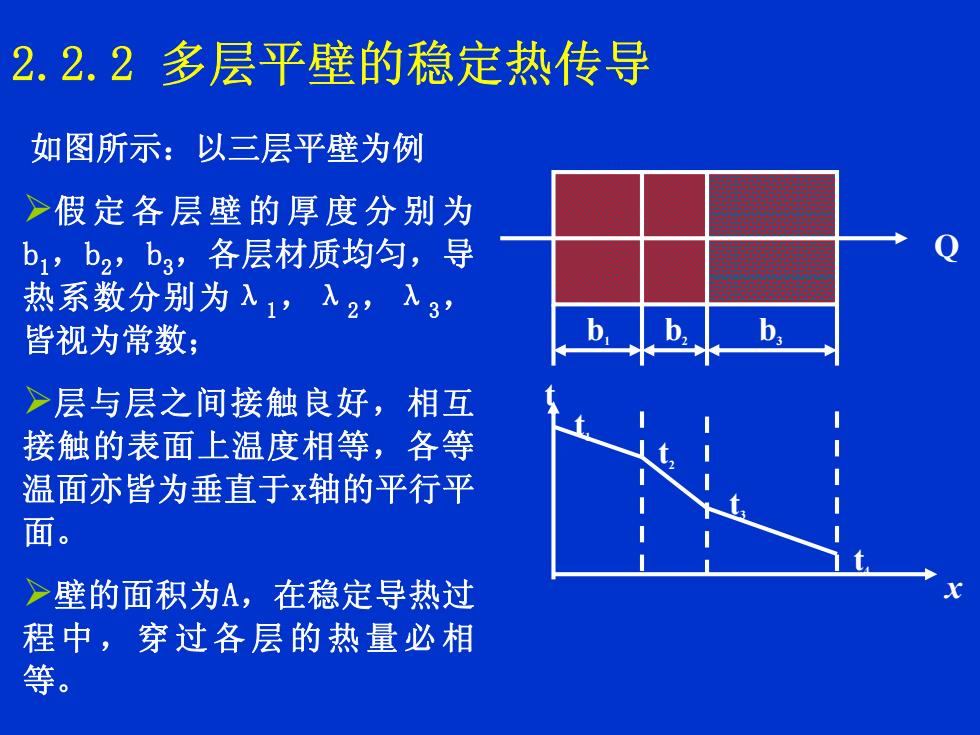
2.2.2多层平壁的稳定热传导如图所示:以三层平壁为例假定各层壁的厚度分别为bi,b2,ba,各层材质均匀,导热系数分别为,2,入3皆视为常数;层与层之间接触良好,相互接触的表面上温度相等,各等温面亦皆为垂直于x轴的平行平面。>壁的面积为A,在稳定导热过程中,穿过各层的热量必相等
如图所示:以三层平壁为例 Q b1 b2 b3 x t t1 t2 t3 t4 ¾假定各层壁的厚度分别为 b 1,b 2,b 3,各层材质均匀,导 热系数分别为λ 1,λ 2,λ 3 , 皆视为常数; ¾层与层之间接触良好,相互 接触的表面上温度相等,各等 温面亦皆为垂直于x轴的平行平 面。 ¾壁的面积为A,在稳定导热过 程中,穿过各层的热量必相 等。 2.2.2 多层平壁的稳定热传导

第一层(t) - t2 qbbti - t = Atib,第二层=△t29222b3第三层三△t39323对于稳定导热过程:qi=q2=q3=qAti+At,+At导出依据:在稳定传热时,通过各层的热流密度必然相等
)(q 21 1 1 1 tt b −= λ 21 1 1 1 q 1 ttt b Δ=−= λ 3 3 3 q 3 t b Δ= λ 2 2 2 q 2 t b Δ= λ 第一层 第三层 第二层 对于稳定导热过程:q1=q2=q3=q 321 3 3 2 2 1 1 (q ) ttt bb b Δ+Δ+Δ=++ λλλ 导出依据:在稳定传热时,通过各层的热流密度必然相等

tyA△t-t60b元2元At +At, + At3t, -tR, + R, + R3R +R + R同理,对具有n层的平壁,穿过各层热量的一般公式为t, -tn+1 -t-tn+R式中i为n层平壁的壁层序号
( () ) q 3 3 2 2 1 1 41 3 3 2 2 1 1 1 2 3 λλλλλλ bb b tt bb b ttt ++ − = ++ Δ + Δ + Δ = 321 41 321 321 q RRR tt RRR ttt ++ − = ++ Δ + Δ + Δ = ∑∑ = + = = + − = − = n 1i i 11 1 11 R q n ni i i i n tt b tt λ 同理,对具有n层的平壁,穿过各层热量的一般公式为 式中i为n层平壁的壁层序号