
第十九章教学基本要求 第十九章振动 x=Acos(ot+o) U-c@t+o+号 a=Ao2c0s(ot+p+元) 频率相同 0 振幅的关系 Vn=Ao am=Ao 相位差 超前 落后
第十九章 教学基本要求 第十九章 振动 频率相同 振幅的关系 m = A 2 am = A 相位差 超前 落后 x = Acos(t +) = + + 2 π A cos t cos( π) 2 a = A t + +
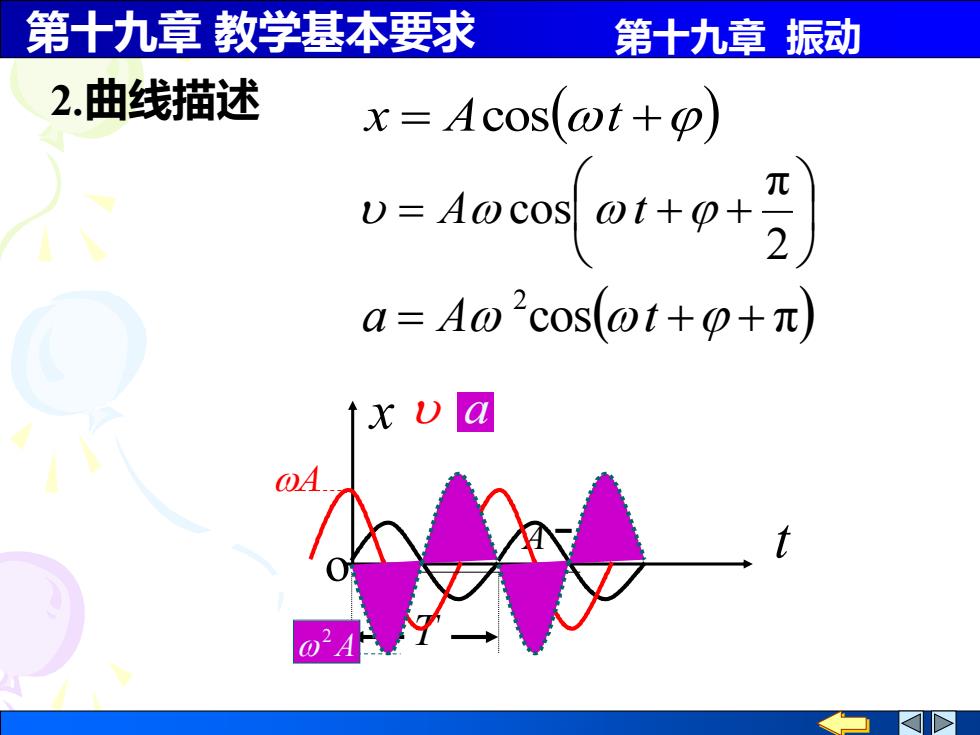
第十九章教学基本要求 第十九章振动 2.曲线描述 x Acos(wt+o) -doc a=Ao2cos(ot+p+元) ↑xa @A
第十九章 教学基本要求 第十九章 振动 2.曲线描述 x = Acos(t +) = + + 2 π A cos t cos( π) 2 a = A t + + T o x t A A a A 2

第十九章教学基本要求 第十九章振动 3.旋转矢量描述 >用匀速圆周运动表示简谐运动的位置变化。 设一质点沿圆心在0点而半径A的圆周作匀速运动, 其角速度为0 规定 7- A t+p X 设质点的径矢经过与 X x轴夹角为0的位置 开始计时,则在时刻t此径矢与x轴的夹角0t+p 质点在x轴上的投影式x=AC0s(ot+p)
第十九章 教学基本要求 第十九章 振动 t 3. 旋转矢量描述 ➢用匀速圆周运动表示简谐运动的位置变化。 规定 x o A A = A x 质点在x轴上的投影式 x = Acos(t +) t + 设一质点沿圆心在O点而半径A的圆周作匀速运动, 其角速度为 。 设质点的径矢经过与 x轴夹角为 的位置 开始计时,则在时刻t此径矢与x轴的夹角为 t +

第十九章教学基本要求 第十九章振动 其与简谐运动的定义公式相同。 所以,做匀速圆周运动的质点在某一直径上(x轴) 的投影的运动就是简谐运动。圆周运动的角速度就 等于振动的角频率,圆周的半径就等于振动的振幅, 初始时刻作圆周运动的质点的径矢与x轴的夹角就是 振动的初位相
第十九章 教学基本要求 第十九章 振动 其与简谐运动的定义公式相同。 所以,做匀速圆周运动的质点在某一直径上(x轴) 的投影的运动就是简谐运动。圆周运动的角速度就 等于振动的角频率,圆周的半径就等于振动的振幅, 初始时刻作圆周运动的质点的径矢与x轴的夹角就是 振动的初位相

第十九章教学基本要求 第十九章振动 以0为 当t=0时 A 原点旋转矢 量A的端点 在X轴上的 X 投影点的运 xo =Acos o 动为简谐运 动
第十九章 教学基本要求 第十九章 振动 以 为 原点旋转矢 量 的端点 在 轴上的 投影点的运 动为简谐运 动. x A o x o A x0 = Acos 当 t = 0 时 0 x