
态中最多只能容纳一个粒子,我们取某单粒子量子态作为近独立 子系,应用巨正则系综作同样的处理,但在式(1.70)中,一0,1, 即。 ∑exp(-(e一)n(,r)】 推京 >expt-(e-p)/(T)] ,exp[-(B-)/(kaT)】 (1.73) 1+exp[-(e一4)/kT] 或 1 (1.74) exp[(e-)/(kT)]+1 将式(1.71)及(1.74)合并,有 1 “-”Bose子 exp[(e一)/(kaT)]士1l“+”Fermi子 (1.75) 这便是上述两种量子统计的主要结果 四、电子气的微观运动状态和它对热容的形响 电子的自旋量子数m,一,因此,它服从Fermi--Dirac 统计。电子在金属中的运动,可看作是电子气的运动。但其质量 须取有效质量,可以是电子质量的数倍或若干分之一,一般由实验 确定.因此,人们把金属中的电子称为准自由电子 在金属的体积V内,在动量区4p的球壳内的单粒子量子 态数目,由式(1.23)给出 △Wm2Y4xp2dp (1.76) 因p2/2m一6,或pV2m6,代入上式得到在能量在6至6十 d的量子态数 。20·
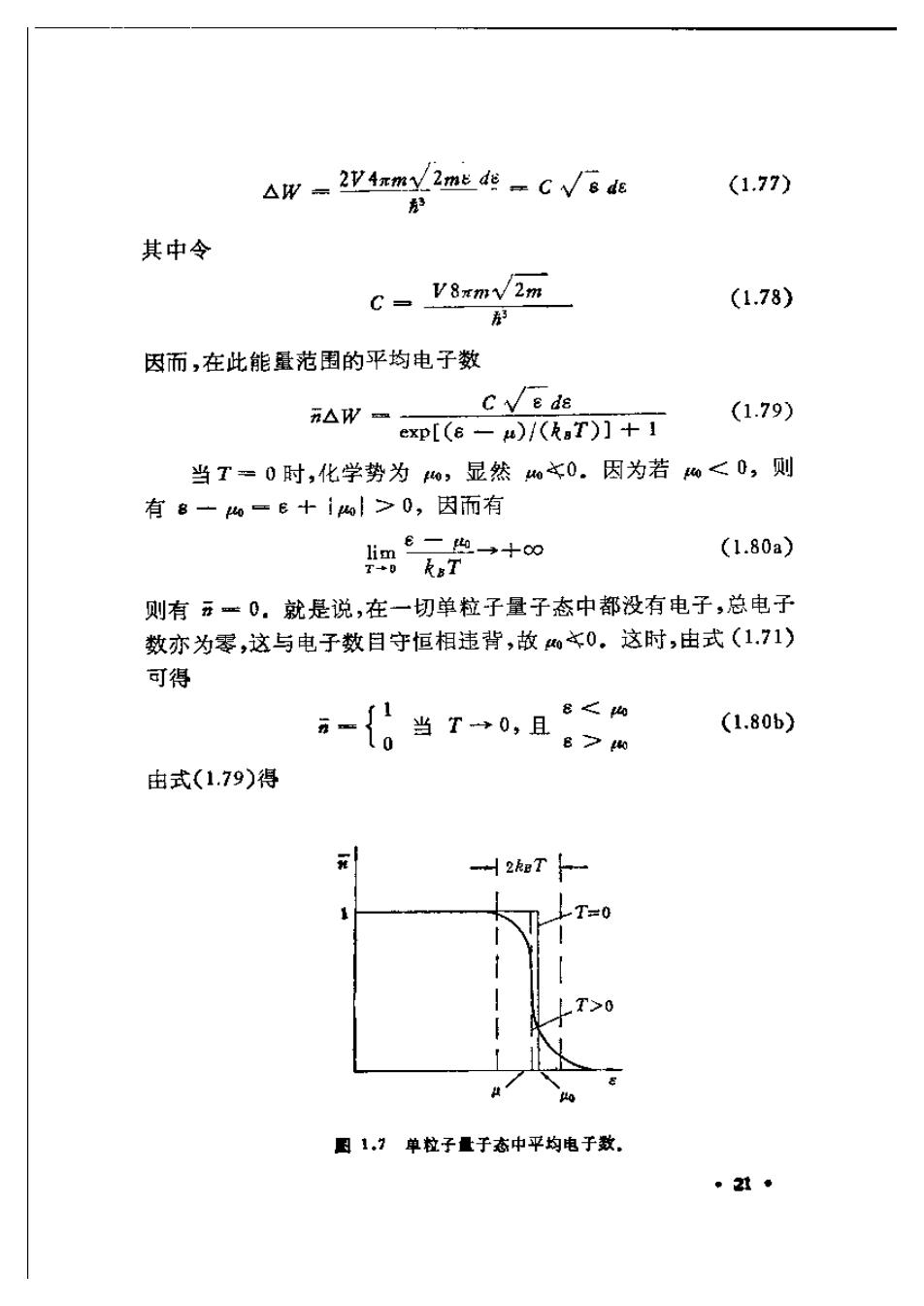
△w=2y4rmY2m&de=C√/8d6 (1.77) 为 其中令 C- V8xmV2m (1.78) 因而,在此能量范围的平均电子数 CVeds n△Wm (1.79) xp[(6-B)/(RaT)]+1 当T=0时,化学势为0,显然0本0.因为若<0,则 有8一w=e十}>0,因而有 €一典→+0∞ 四kT (1.80a) 则有元=0。就是说,在一切单粒子量子态中都没有电子,总电子 数亦为零,这与电子数目守恒相违背,故0本0。这时,由式(1.71) 可得 当0,且 (1.80b) 由式(1.79)得 小2知T T=0 因1.7单拉子量子态中平均电子数 ·2就

C./ >0 .T=0 440 图1.8电子按能最的分布. AW 当T→0,且 <o (1.81) >w 由式(1,80b)可见,当e<%时,单粒子量子态中都被一个电子占 据着,即全充满。而在6>%时,则所有量子态全空着。单粒子 量子态中的平均电子数和电子按能量的分布,如图1.7和1.8所 示 这样,在T=0时,以%为界,把能级划成两部分。8<的 能级中全充满电子(每个单粒子量子态包含一个电子);6>的 能级全空着;而&▣.的能级称为Fermi能级.从总电子数 N,可通过式(1.79)求出 0· N-ic5 de-jc√⑧6-c子心 16πm√2m 3 (1.82) 则 3 Ni 2m (1.83) 8 V 22*

:电子的平均动能豆和总动能E分别为 E-(ae)c√Bde-Cevds -cm-是 (1.84a) 5 范3 (1.846) N5 以上讨论的是T=0时情况。此时电子气只有一个微观运 动状态,即“Fermi能级以上全空,Fermi能级以下全满”的运 动状态,别无经历其他微观态的可能。 当T>0时,按照式(1.82)及(1.84)第一个等式来计算。此 时,有一小部分电子跑到Fermi能级以上的能级中,而Fermi能 级以下的能级又空出一部分。因此,电子的平均动能比T=0时 增加了一些热运动的能量.此时(参见图17,1,8), - (1.85a) 范≈3地十定(T)》 (1.85b) 5 电子气对恒容热容的贡献为 -().-1¥. =N项东&辽 (1.86) 2 在室温下,sT/%心102一10-3.所以,和%的差为110一 1/10?,电子气对热容的贡献是金属中离子振动对热容的贡献的 1%,因此,在室温条件下可将其忽略。这就是通常在讨论热容时 不考虑电子的贡献的原因。 $1.5偏差与涨落现象 体系的宏观物理量是由体系的微观态相应物理量的统计平均 ◆23

而求得的.在数理统计中,一组测量值与平均值之间存在偏差,在 分子热力学中,称其为涨落。 体系在某一瞬时,处在某一微观状态,其对应的物理量为P: 经过一组测量后,可得平均值 Fi/N (1.87): 则方差S为 (F-F)/(N -1) (1.88). 如果测置值的分布符合正态分布(N+∞),方差的数学期望是 标准方差,平均值的数学期望是真实F。·即有 E(F)=F。 (1.89) E(S2)=o2 (1.90) 其中, N (1.91) 四1 。又称为标准误差。一组测量值可用 (F,F2,·,Fw)N(F0o) 来表示。由于这里所讨论的体系,N值很大,故标准误差。与方差 S是一样的S是表示微观量偏离平均值的误差,可称为绝对涨 落 S-√-√:-)2 (1.92) 将相对误差或变异系数 S (F一F2 (1.93) 称为相对涨落。同样,对于平均值下,它也是个随机变量。在数理 统计中可表示为 F~N(F,02/N) ”21