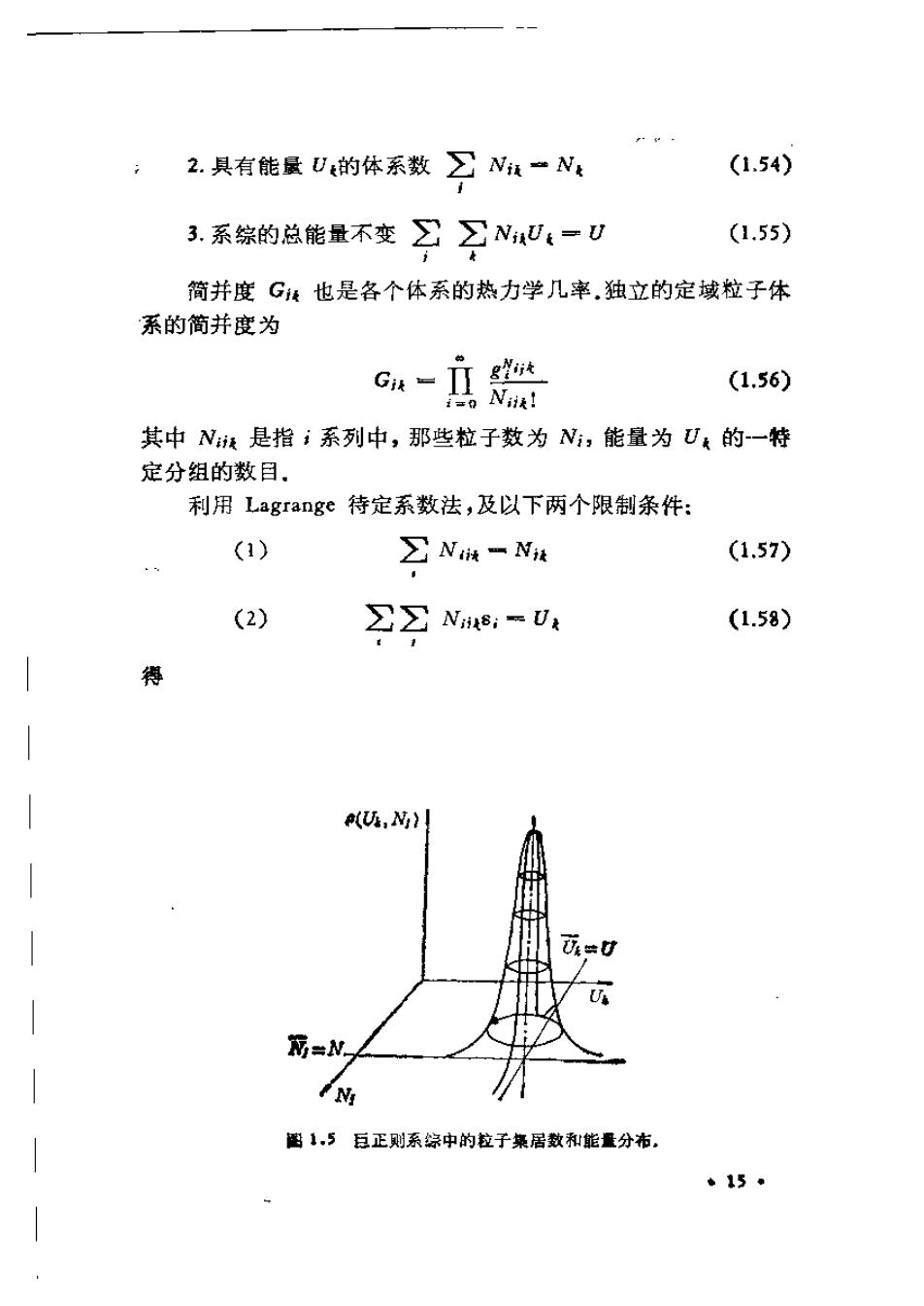
;2.具有能量U的体系数 ∑N=N (1.54) 3.系综的总能量不变 NiV-U (1.55) 简并度G,也是各个体系的热力学几率.独立的定域粒子体 系的简并度为 giik (1.56) i=0 Niik! 其中是指系列中,那些粒子数为Ni,能量为U的一特 定分组的数目. 利用Lagrange待定系数法,及以下两个限制条件: (1) ∑N一N (1.57) (2) 2∑Ne,=0 (1.58) 得 1 1 , NEN /Ni 图1.5豆正则系粽中的拉子集居数和能量分布。 +150

N政= Giep(二N-BU&) (1.59) N ∑∑GixexP(-aW,-8Ux) 其中 (1.60) 故式(1.59)可写为 N达a Gexp[(N;一Ut)/(aT)] (1.61) N ∑∑GicXP[(N;-U)/(aT)] 上式分母称为巨正则配分函数: 8=∑∑Gexp[(w-U)/(gT)](1.62) 这样,对于独立的定域粒子体系的巨正则配分函数为 8- 22Ⅱ N (1.63) 如果把式(1.62)改写成 s-2exn(Y儿习c:e(-&】 上式右边括号项就是一个含有W;个粒子的体系的正则配分函数 Q,所以式(1.62)可写成 B-空0,ew(x) (1.64) 从式(1.64)可以得到 s-ew(月 (证明从略) (1.65) 即将式(1.64)中加和值可用其中最大组元来代替.由于W一 G,故有 ◆16◆

inin ✉P kgT AaT G RgT kaT 或 n8一,PW=Z(压缩因子) (1.66) kaT 或 PV(T,V,u)-ksTin(T,V,u) (1.67) 则 s-221-r (i.68) U-RaT? alnΞ (1.69) §1.4近独立非定域子系的量子统计 一、3种统计的异同 上述讨论的体系都是由同一类粒子所组成的.同一类粒子 具有全等性,即两个粒子互相交换各自所处的状态并不改变体系 的微观状态。因而这类粒子是不可识别的。但是,对于定域子系, 每个粒子只在自己独有的小范围空间内运动,因而可以通过不同 的空间位置来识别它们,即可通过编号1,2…来分辨。Maxwell- Boltzmann定域子系分布就是这样的.但是,将它用于气体,又 认为粒子是不可分辨的。对于Maxwell--Boltzmann统计处理这 两种情况时,其热力学几率相差N!,这都属于经典统计 量子统计有Bose-Einstein统计和Fermi-Dirac统计,它们 都是非定域子系的,粒子是不可分辨的.在Bose-Einstein统计 中,粒子不遵守Pauli不相容原理,即可以允许任意多的粒子处 于同一量子态。通常自旋量子数为整数的粒子,如光子、π介子和 He;等符合此条件,故称它们为Bose子(Boson).而在Fermi- Dirac统计中,粒子必须遵守Pauli不相容原理,即一个量子态至 ◆17

多允许一个粒子存在,通常自旋量子数为半奇数(1/2,3/2,5/2)的 粒子符合此条件,故称之为Fermi子,如电子、质子、中子和Hc, ·O等。 包60ù自d0自 日日.00日日000 A:Bose--iastein镜t 包回00包包回0日 B.Fermi--Dirac桃计 00 可 C.MXwe-Bolt2 mann徒计 图1.63种统计方法示意图, 这3种统计的区别,可用图1.6来表示:对于有2个粒子及3 种粒子状态的体系,用Bosc-Einstein统计,体系的微观状态数目 是6个;用Femi-Dirac统计,体系的微观状态数目是3个,以上 粒子皆不可分辨,故用全同黑点表示;而用Maxwel-Boltzmann统 计,体系的微观状态数则是9个,由于粒子是可分辨的,故用圆圈 和点分别表示之。显然这3种统计是有明显差别的.但是除电 子、光子等极轻粒子以外,在不太低的温度(~10K)下,对于由原 子、分子等组成的气体体系,用3种统计所得结果是一致的。这是 由于Maxwell--BoItzmann统计处理气体时,按非定域子系处理,则 不可分辨;而粒子密度不高时,平均地看,绝大多数量子态都是“空” e18·

的,多个粒子挤在一个量子态的情祝极少发生,即使出现这种情 况,Paui不相容原理也不起作用,因而这3种统计的差别就显示 不出来。 1 二、Boae-Einstein统计 B0s心子是允许同一量子态有数个粒子,可视为子系,按照巨 正则系综来处理 Gitexp[(W;一U)/T] I N达= (1.61) ∑∑Gixp(N,-U)/,T] s 由于我们讨论的是子系,故可取掉下标,在此能级有”个粒子 (r=0,1,2,…),故U一U一e。/N是指出现a个粒子 的几率,并考虑到是非简并态(即G:一1)。在某个量子态中的 平均粒子数m则应该是几率乘以粒子数的总和,用下式表示 ∑ep[-(e-)n/(k,T)】 月共0 exp[-(s一4)#/(kaT)] 0 e-(s-e水T) expI-(6 -#)T (1.70) 或 (1.71) exp[(e一/(sT)]-1 而该单粒子量子态中的平均能量为 至=aB= expI(s-u)/(kT)]-1 (1.72) 这就是Bose-Einstein统计的主要结果. 三、Fermi-Drac统计 对于服从Pauli不相容原理的Fermi子,每个单粒子量子 ●19