
2.正则系综(canonica1 ensemble) 组成正则系综的各力学体系间是由一块刚性的、非渗透的,但 可以传热的隔板隔开的。如图1.26所示.此时,每个体系的T,7 和N都是不变的常数,但各力学体系之间有能量传递,好像把体 系置于一个恒温槽中一样 3.巨正则系综(grand canonical ensemble) 组成巨正则系综的各力学体系闻是由“块刚性的、可传热和 可渗透的隔板隔开的.如图12c所示。此时各力学体系的T,V 和化学势“都是不变的常数。但是,各体系之间可以有能量和质 量的传递。 二、微正则系综及其热力学公式 对于系综的一种分布,它所包含的微观状态数目,称之为热力 学几率W w (1.30) 式中&:是三微观态的权重,对应于同一微观物理量:状态的数 目.该系综所有可能(又称可及)微观状态的数目Q,应对各种不 同的分布进行总的加和: 。-3赔 (1.31) 此式应用于有N个粒子的体系中,N:表示为能量等于:的粒子 数,g:为能级主的统计权重或简并度,{N}是满足下列两个限制 条件时所有可能的N:的总和 粒子总数不变: Ni=N (1.32) 。10
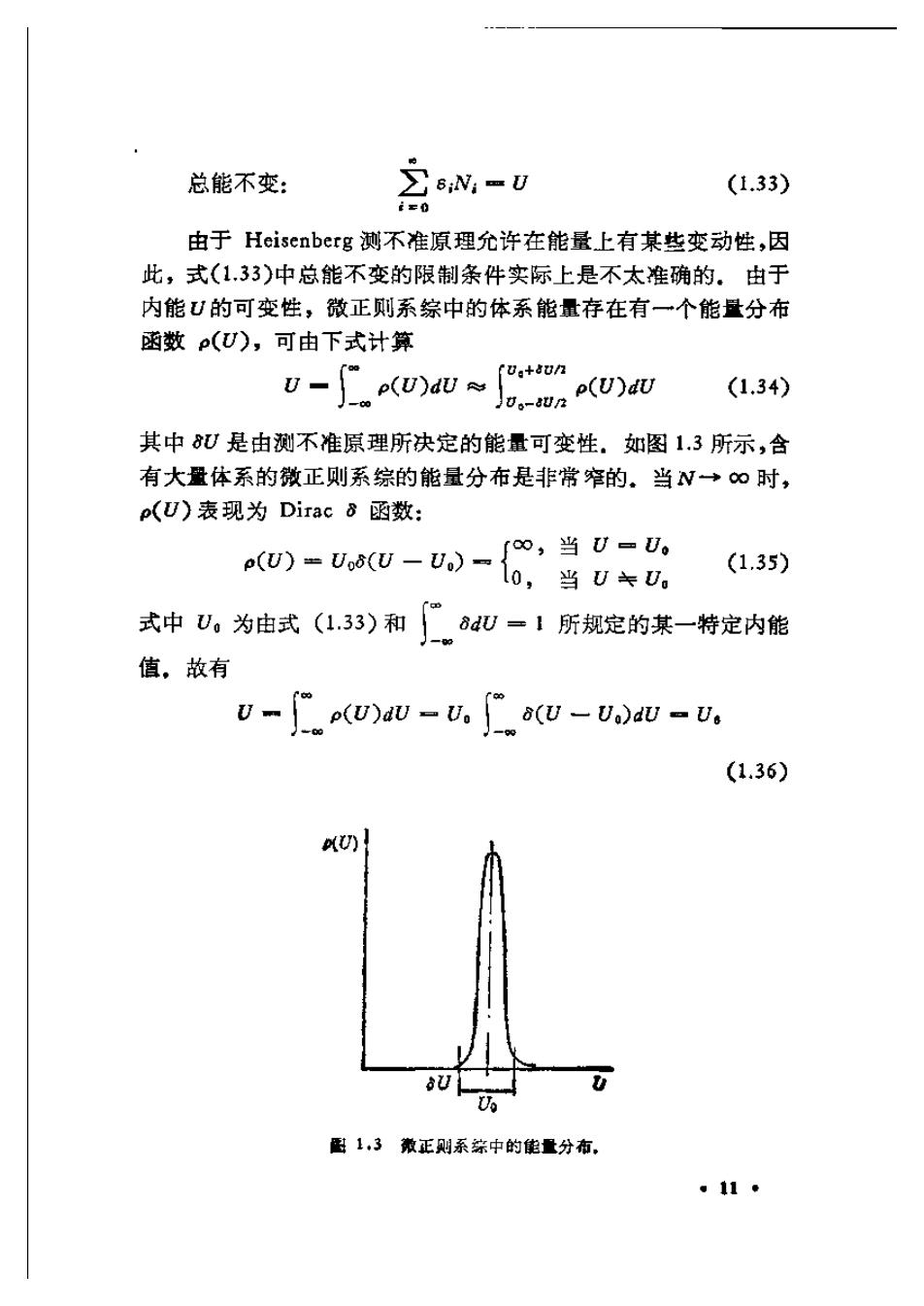
总能不变: B;Ni-U (1.33) i=o 由于Heisenberg测不准原理允许在能量上有某些变动性,因 此,式(1.33)中总能不变的限制条件实际上是不太准确的.由于 内能的可变性,微正则系综中的体系能量存在有一个能量分布 函数p(U),可由下式计算 U-w)≈ [0:+8on Joo-oun (U)du (1.34) 其中U是由测不准原理所决定的能量可变性。如图1.3所示,含 有大量体系的微正则系综的能量分布是非常窄的。当N→∞时, p(U)表现为Dirac8函数: P(U)=U08(U-U)- o,当U=U。 l0,当U卡U (1.35) 式中U。为由式(1.33)和84U=1所规定的其一特定内能 值。故有 U-(U)du-v.aQ-v)du-v. (1.36) dU) 图1,3兼正则系综中的能量分布。 11

微正则系综中所有可及微观状态总数口又可称为微正则配分 函数。显然它可表示为U,V和N的函数: 0=Q(U,V,N) (1.37) 而体系的熵函数 S-5(U,V,n) (1.38) n为摩尔数.N-Na·n,Na为Avogadro常数。所以,S与O 的变量是相同的.Boltzmann提出的公式 S(U,V,n)-kaIn Q(U,V,N) (1.39) 表示了它们之间的内在联系。式中为Boltzmann常数。这 是一个系综的统计性质和宏观性质相联系的基本公式. 准确计算出Q也是相当困难.因此,Darwin和Fowler切用 严格的方法成者Rushbrooke用简单的方法,都可得到 ln0≈ln形a: (1.40) Q是所有可能的分布的微观状态数总和,但所有可能的分布中, 必有一个最可几分布,它所对应的微观状态数目最多。Wx即是 最可几分布的微观状态数或热力学几率。这样,由式(1.39)可得 S=kaln W max (1.41) 由热力学基本方程可得Helmholtz自由能函数A A✉U一TS (1.42) 又 方-(8》w 则得 A-r(停-)-(u8-s/八) -8(/八器) (1.43) oln Q

此方程在形式上有一定的对称性 三、正则系综及其热力学公式 对于正则系综,限制条件为 N-N (1.44) i=0 会N,-U (1.45) 其热力学几率 w -N i别 (1.46) 以上各式中,简并度G,表示系综中有N;个体系占有U;能级 的方式数.处于能级U;的体系分数N/N为 Nj-_ Giexp(-AUi) (1.47) N 2 Giexp(-BUi) 式中m G;exp(--BUi) (1.48) 为正则配分函数。当体系是由独立的定域粒子组成时,其正则 配分函数为 Q-会会器如(-会N (1.49) 正则系综的能量分布如图1.4.当N足够大时,能量分布就很 集中了 正则系综的热力学公式为 s-h2+ (1.50) 。13

)} a<b<c N=c N=b. 图1.4正则系粽中的能量分布. A=-ksTin Q (1.51) 四、巨正则系综及其热力学公式 以上我们讨论的是粒子数不变的情况。假如体系与外界有粒 子数交换或者体系内发生化学反应时,则它的分布除了与能量有 关外,还与体系中的粒子数有关,如图1,2c所示,这种系综就是巨 正则系综巨正则系综的总能U和粒子总数是不变的.但系综中的 各体系的能量和粒子数,由于相互之间有交换,故是可变的。但 是,各体系的温度T,体积V及化学势“都是相等的 巨正则系综的能量分布p(U,N)与粒子集居数N,之间关系 见图1.5. 巨正则系综的热力学几率 立i姓 (1.52) 00N 式中N,为具有能量为U:和粒子数为N;的体系数。对于此 式,限制条件为: 1.系综总粒子数不变∑》NN,一N (1.53) 单14e