
须是单值函数才有意义。因而,经过相空间中的任一点的相轨线 只有一条. 由于保守力系的总能E不变,故可得下式 H(1,92,,9f;P1,P2,··,P)=E (1.17) E为运动常量,是正则运动方程的积分常数、式(1.17)代表一个 一1维的曲面,称其为能量曲面。保守力系在相空间中的代表 点运动而成的相轨线一定在此能量曲面上.对于化学反应体系,人 们所关心的主要是体系的势能曲面,或称势能面.反应体系的 代表点随着反应的进行而形成的轨线,称为反应轨线W。它一定 位于势能面上, 相空间的一部分称为子相空间,如由(91,92,··,4)或由 (p,2,··,)形成的空间是子相空间.单个粒子的广义坐标 (91,92,)及广义动量(1,P2,)形成的空间,相对于体系来 说,它是子相空间,故又称之为空间. 二、量子力学的运动状态,量子态 量子态与经典力学的微观态概念是不同的.每一个定态可用 一组量子数表示。例如,电子有3个平动自由度及1个自旋自由 度,于=4,就需用4个量子数来描述它的一个量子态。用量子数 来标志,反映出两个特点:1.能量的不连续性,每一个被允许的 能量值称为能级。2.同类粒子的全等性,即处于不同状态的两个 粒子交换位置;不改变体系的微观状态.全等性的重要意义在量 子统计和涨落问题中是很明显的.但对于经典统计,粒子的全等 性效果不显著 在一定条件下,如果同类粒子的全等性效应可以忽略,以及能 级的不连续性也可忽略,则量子统计就过渡到经典统计, 设一边长为L的密闭立方盒子。根据量子力学,在盒子中平 动的单个粒子,可用量子数,,:来描述其运动,它的能量为 E-《经+(臣矿+(经} (1.18) 5

--- 而其动量分量为 「t0,±1,±2··】 p=,白一2h,=,{m,。0,士1,士2… L (nx=0,±1,士2. (1.19) 将式(1.19)代入式(1.18)得 E=1[p:+p%+p] (1.20) 2m 上式在形式上与经典力学中动能公式相同, Tem粒一(+巧+) 22 1[p+pg+p] (1.21) 2m 但是,在经典力学中,能量值是连续的,而在量子力学中,E是不连 续的,只能取式(1.19)所规定的数值.用动量空间来表示,就只能 0.0.90000 000000000 0000$0000 00口0p0000 0068◆日-自0日“ ◆ 900 Pa 口0000 0000 000 0009 图1,上平动壁于态所可能对应的动量空间的代表:。 取如图1.1中代表点的值,是一些间断点,图中每两个相邻代表点 的距离为/L,因此,平均来说,每个代表点所占动量空间的体 积为(/L).而它在坐标空间所占的体积为L3,这个粒子在相 空间中所占体积为前二者乘积 (/L)L3= (1.22) 6

所以,对于自由度为手的体系,在相空间占有的体积。这可以 用BWK方法W导出.这就是相格的概念。要计算在相体积中有 :几个量子态,可用公式 △o=△4△92△94Ap1△p2…△25 (1.23) 时 即在这个相体积中相当于有△山个量子态。式(1.23)只是在计 算量子态的数耳上才是正确的。其实,量子态所描述的微观运动 一般并不局限于相体积中活动,只有势场变化不很快的情况下才 能近似地这样认为. 对平动来说,两个相邻能级,An.=1,△,一△#x一0之 间的能量差为[由式(1.18)] AE。12 (2x+1) (1.24) 2m Li 可见L越长,能级差越小。如质量m一0.103×10-”g的电子 在Lm0.01cm立方体中运动,则 1h2 (6.61×10-7)2 2mL22×0.9103×10-×(0.01)2 ≈2.510-2erg≈1.5X10-eV 当T=300K时,aT的值为1/40V,T=3K时,mT≈,1eV. 4000 这就是说,在相当低的温度下,:T的数值仍然比平动能级差大 得多。故能级的不连续性可以忽略。对于微观粒子的平移运动, 用经典统计和用量子统计处理,其差异是可以忽略的。这就是说, 从量子统计过渡到经典统计。对于其他形式的运动,只要能级差 比sT的数值小得多时,均是如此. §1.3统计系综和热力学公式 计算体系微观物理量平均值的两种方法:按时间平均与按系 综平均

若按时间平均,则需要翔道时体系处于第主个微观状态的 时间总和△.当然,此处△是体系各次停留时间的总和.我们为 此进行了N次测量,发现有N:次是处第i个状态.显然,当W→ o,t时,这二者分别表示为体系处于i状态的几率(): p()=im:-in红 (1.25) N-N 这样,平均值 京-∑(i)F: (1.26) 式中F:是体系处于状态时的物理量数值, 显然,从统计的角度看,我们对一个体系进行N次观察的结果 和同一时刻对N个性质完全相同的体系在相同条件下观察的结果 是一致的.这种N个体系的集合称为系综.从式(1.25)(1.26)可 知,按系综平均与按时间平均是完全一致的。{N:}就是所讨论的 系综中体系的分布数目。{:}是离散型函数,在数学处理上不太 方便。因此,我们通过相空间来处理。当然,当N→o时,这两者 的结论是一致的. 设体系某一微观物理量F是相空间上一个连续函数:F一 产(91,92,·,财p1,P2,·,)。对应的微观态在相体积元d红中 出现的次数为pdr. ∫dr-∫…dqdqr…dgy;dp,dpa…d4 (1.27) p=p(9192··9tp1,P2·Pf) (1.28) P是体系某一微观状态在相空间(g,42,··,f;p1,p2,,P)单 位体积元中出现的次数,是密度函数.在分子热力学中称为分布 函数。这样平均值 Fpdr (1.29) pdr
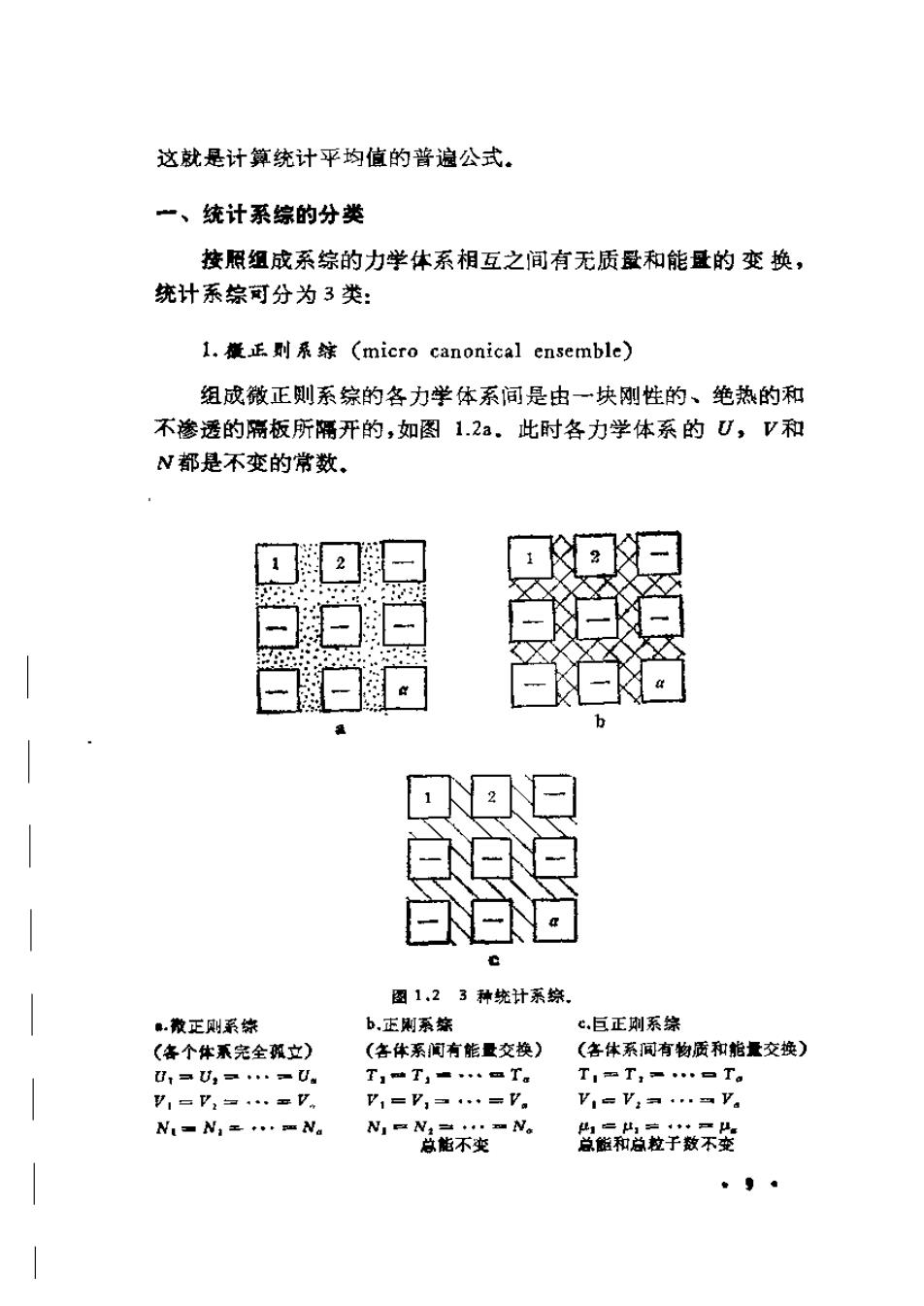
这就是计算统计平均值的普遍公式。 一、统计系综的分类 按照组成系综的力学体系相互之间有无质量和能盘的变换, 统计系综可分为3类: 1,樣正则系嫉(micro canonical ensemble) 组成微正则系综的各力学体系间是由一块刚性的、绝热的和 不渗透的隔板所隔开的,如图1.2a.此时各力学体系的U,V和 N都是不变的常数、 独 b ENN 图1.23种统计系综 。撒正则系综 b.正则系笨 c,巨正则系综 (各个体系完全翼立) (各体系间有能量交换) (各体系间有物质和怡量交换) 0:aU2·=U T1陆T,=mTa T,mT,=…T。 ,=V,一…=P V,=V,▣·=a V,=V,…ay。 N=N,x·mNa NIE N1=..>No 1==··=。 总能不变 总脑和总粒于数不变