
二、二阶系统的单位脉冲响应)和单位阶跃响应 在不同阻尼系数下,二阶系统的单位脉冲响应和单位阶 跃响应如表3.4.1所示。 表3.4.1二阶系统的单位脉冲响应w)和单位阶跃响应 阻尼系数 单位脉冲响应() 单位阶跃响应 5=0 x()=1-cos0,1 无阻尼 w(t)=@,sin@t 0<5<1 es如a 1 欠阻尼 ()=- x(1)=1-e-i_ 5=1 w))=ote x()=1-(1+o10e 临界阻尼 >1 x0= x(0=1 o。ee 过阻尼 2g9- 其中,o4=0nV-2,称o。为二阶系统的有阻尼固有频率: 5=-(5+V2-1)m:52=-(5-V2-1)m。 当取值不同时,二阶欠阻尼系统的单位脉冲响应曲线如图 3.42所示。由图可知,欠阻尼系统的单位脉冲响应曲线是减幅 的正弦振荡曲线,且5愈小,衰减愈慢,振荡频率四愈大。故欠 阻尼系统又称为二阶振荡系统,其幅值衰诚的快慢取决于和。 (光称为时间衰减常数,记为。):
二、二阶系统的单位脉冲响应w(t)和单位阶跃响应 在不同阻尼系数下,二阶系统的单位脉冲响应 和单位阶 跃响应如表 3.4.1 所示。 w(t) 表 3.4.1 二阶系统的单位脉冲响应 w(t) 和单位阶跃响应 阻尼系数 单位脉冲响应w(t) 单位阶跃响应 ξ = 0 无阻尼 w t t ω n ω n ( ) = sin x t t o ω n ( ) = 1− cos 0 < ξ < 1 欠阻尼 w t e t d n t n ω ξ ω ξω sin 1 ( ) 2 − − = ) 1 sin( 1 1 ( ) 1 2 2 ξ ξ ω ξ ξω − + − = − − x t e d t arctg t o n ξ = 1 临界阻尼 t n n w t te ω ω − = 2 ( ) t o n n x t t e ω ω − ( ) = 1− (1+ ) ξ > 1 过阻尼 ( ) 2 1 ( ) 2 1 2 n s t s t o x t e − e − = ξ ω ( ) 2 1 ( ) 1 1 2 2 1 2 s e s e x t s t s t n o − − − − = + ξ ω 其中, 2 ω d = ω n 1−ξ , 称 ω d 为二阶系统的有阻尼固有频率; n s (ξ ξ 1)ω 2 1 = − + − ; n s (ξ ξ 1)ω 2 2 = − − − 。 当 ξ 取值不同时,二阶欠阻尼系统的单 位脉冲响应曲线如图 3.4.2 所示。由图可知,欠阻尼系统的单位脉 冲响应曲线是减幅 的正弦振荡曲线, 且 ξ 愈小, 衰减愈慢, 振荡频率 ω d 愈大。 故 欠 阻尼系统又称为二阶振荡系统,其 幅值衰减的快慢取决于 ξω n ( ξω n 1 称为时间衰减常数,记为 σ )
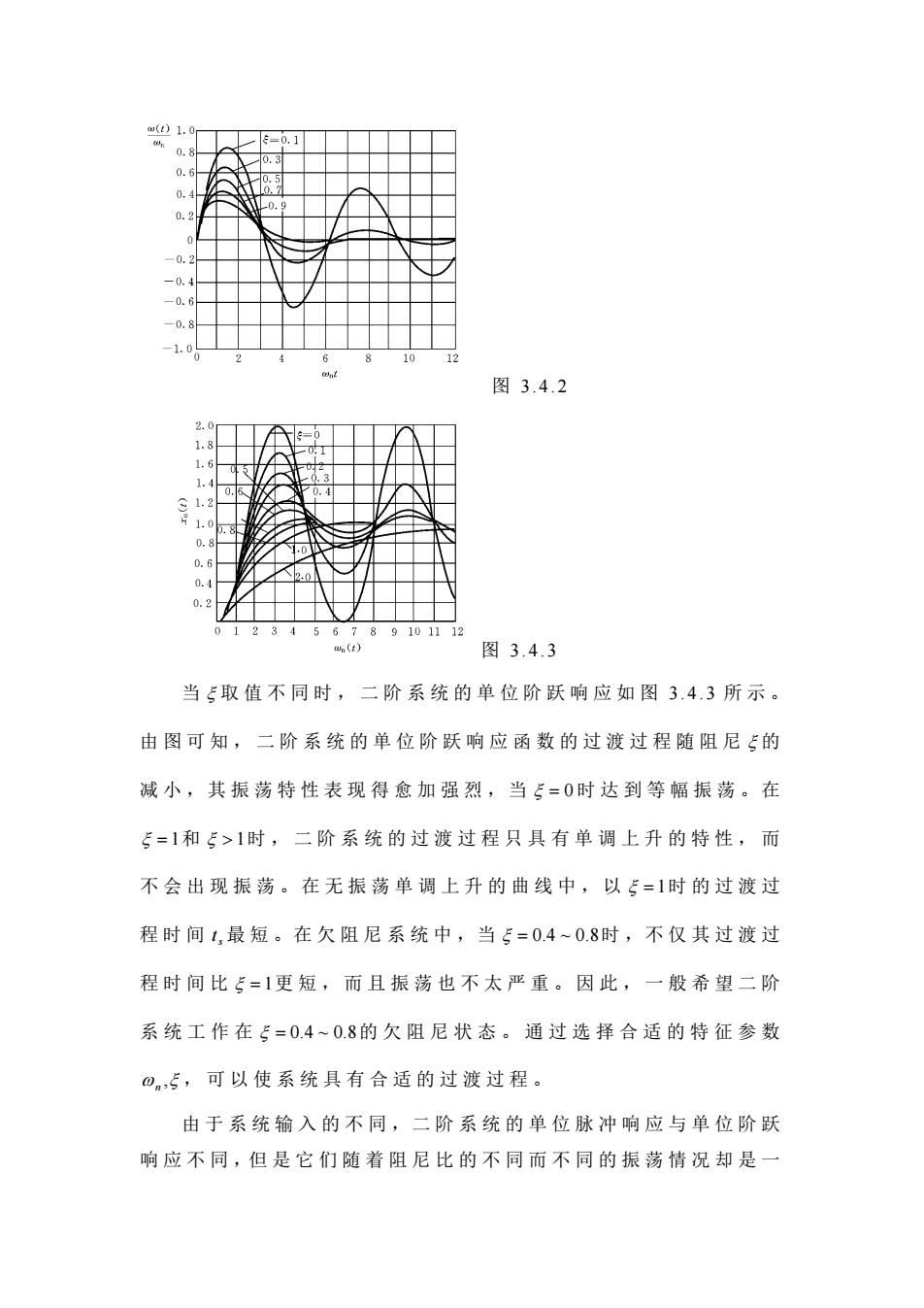
图3.4.2 912345 89101112 图3.4.3 当5取值不同时,二阶系统的单位阶跃响应如图3.4.3所示。 由图可知,二阶系统的单位阶跃响应函数的过渡过程随阻尼的 减小,其振荡特性表现得愈加强烈,当5-0时达到等幅振荡。在 5=1和>1时,二阶系统的过渡过程只具有单调上升的特性,而 不会出现振荡。在无振荡单调上升的曲线中,以5=1时的过渡过 程时间1,最短。在欠阻尼系统中,当5=0.4~0.8时,不仅其过渡过 程时间比=1更短,而且振荡也不太严重。因此,一般希望二阶 系统工作在ξ=0.4~0.8的欠阻尼状态。通过选择合适的特征参数 ⊙,5,可以使系统具有合适的过渡过程。 由于系统输入的不同,二阶系统的单位脉冲响应与单位阶跃 响应不同,但是它们随着阻尼比的不同而不同的振荡情况却是
图 3.4.2 图 3.4.3 当 ξ 取值不同时,二阶系统的单位阶跃响应如图 3.4.3 所示。 由图可知,二阶系统的单位阶跃响应 函数的过渡过程随阻尼 ξ 的 减小,其振荡特性表现得愈加强烈,当 ξ = 0 时达到等幅振荡。在 ξ = 1和 ξ > 1时,二阶系统的过渡过程只具有单 调上升的特性,而 不会出现振荡。 在无振荡单调上升的曲线中, 以 ξ = 1时的过渡过 程时间 ts 最短。在欠阻尼系统中,当 ξ = 0.4 ~ 0.8时 ,不仅其过渡过 程时间比 ξ = 1更短, 而且振荡也不太严重。 因此, 一般希望二阶 系统工作在 ξ = 0.4 ~ 0.8的欠阻尼状态。通过选择合适的特征参数 ω n ,ξ ,可以使系统具有合适的过渡过程。 由于系统输入的不同,二阶系统的单位脉冲响应与单位阶跃 响应不同,但是它们随着阻尼比的不同而不同的振荡情况却是一

致的。当系统为无阻尼系统时,均为等幅振荡;当系统为欠阻尼 系统时,均为减幅振荡:而当系统为临界阻尼或过阻尼系统时, 均不会出现振荡。 三、二阶欠阻尼系统响应的性能指标 二阶欠阻尼系统的单位阶跃响应曲线如图3.4.4所示,其瞬 态性能指标包括上升时间,、峰值时间。、最大超调量M。、调整 时间1,、振荡次数N等。 1,上升时间(,:响应曲线从原工作状态出发,第一次达到输出 稳态值所需的时间定义为上升时间。 -arctan 1,= 当5一定时,0n增大,1,就减小;当o。一定时,5增大,1,就 增大。 r.( M/不 允许误差 0.05成002 图3.4.4 2,峰值时间t。:响应曲线达到第一个峰值所需的时间定义为峰 值时间。 6品 当5一定时,on增大,1,就减小;当0,一定时,增大,1n就 增大
致的。当系统为无阻尼系统时,均为等幅振荡;当系统为欠阻尼 系统时,均为减幅振荡;而当系统为临界阻尼或过阻尼系统时, 均不会出现振荡。 三、二阶欠阻尼系统响应的性能指标 二阶欠阻尼系统的单位阶跃响应曲线如图 3.4.4 所示,其瞬 态性能指标包括上升时间 、峰值时间 、最大超调量 、调 整 时 间 、振荡次数 等 。 r t p t M p s t N 1.上升时间 :响应曲线从原工作状态出发,第一次达到输出 稳态值所需的时间定义为上升时间。 r t d r t ω ξ ξ π 2 1 arctan − − = 当 ξ 一定时, ω n 增大, tr 就减小;当 ω n 一定时, ξ 增大, 就 增大。 r t 图 3.4.4 2.峰值时间 :响应曲线达到第一个峰值所需的时间定义为峰 值时间。 p t d p t ω π = 当 ξ 一定时, ω n 增大, t p 就减小;当 ω n 一定时, ξ 增大, 就 增大。 p t