《电路理论》课程教学课件（讲稿）第8章 相量法

第8章· 相量法 本章重点 8.1 复数 8.2 正弦量 8.3 相量法的基础 8.4 电路定律的相量形式 首页

第8章 相量法 8.1 复数 8.2 正弦量 8.3 相量法的基础 8.4 电路定律的相量形式 首 页 本章重点

●重点： 1,正弦量的表示、相位差 2.正弦量的相量表示 3.电路定理的相量形式 国

2. 正弦量的相量表示 3. 电路定理的相量形式  重点： 1. 正弦量的表示、相位差 返 回

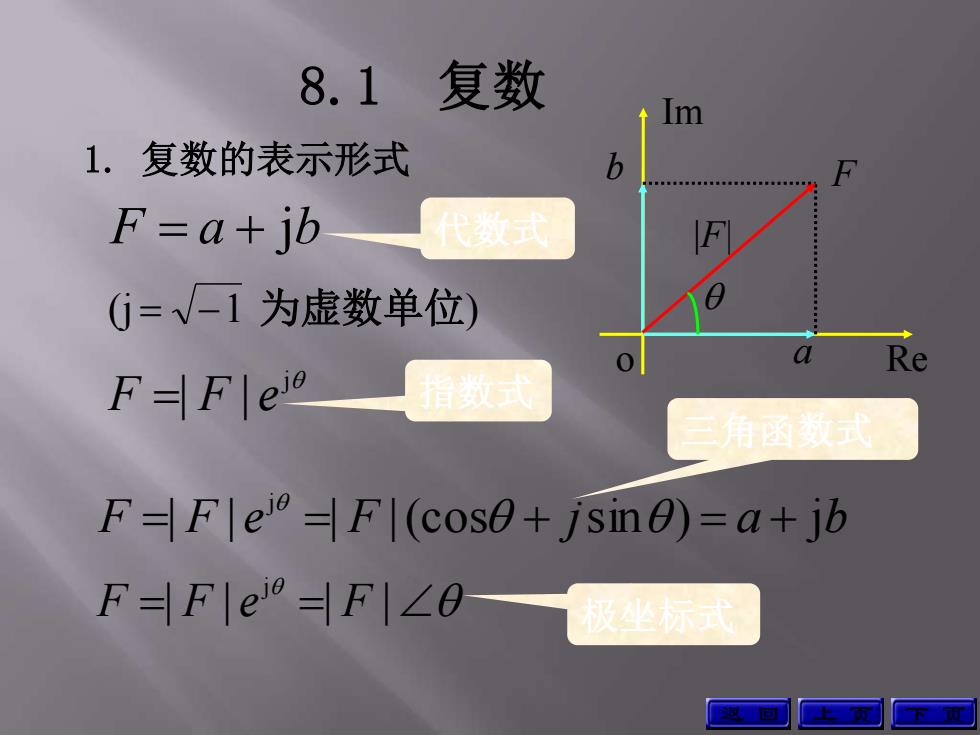
8.1复数 1.复数的表示形式 b F=a+jb 代数式 G=√-1为虚数单位) a Re F=F eio 指数式 三角函数式 F=FleF(cose+jsine)=a+jb FF1eoHF1∠0 极坐标式

1. 复数的表示形式 (j  1 为虚数单位) b F Re Im o a  |F| F | F | e | F |(cos jsin ) a jb j         F  a  jb   | | | |  j F F e F j F | F | e 上 页 下 页 代数式 指数式 极坐标式 三角函数式 8.1 复数 返 回

F=a+jb FF|e°=Fl∠0 IFEVa+b b 或 a=Fcose θ=arctan a 2.复数运算 ①加减运算一 采用代数式

几种表示法的关系：         a b θ F a b arctan | | 2 2 或        | |sin | | cos b F a F 2. 复数运算 ①加减运算 —— 采用代数式 上 页 下 页 b F Re Im o a  F  a  jb |F|   | | | |  j F F e F 返 回

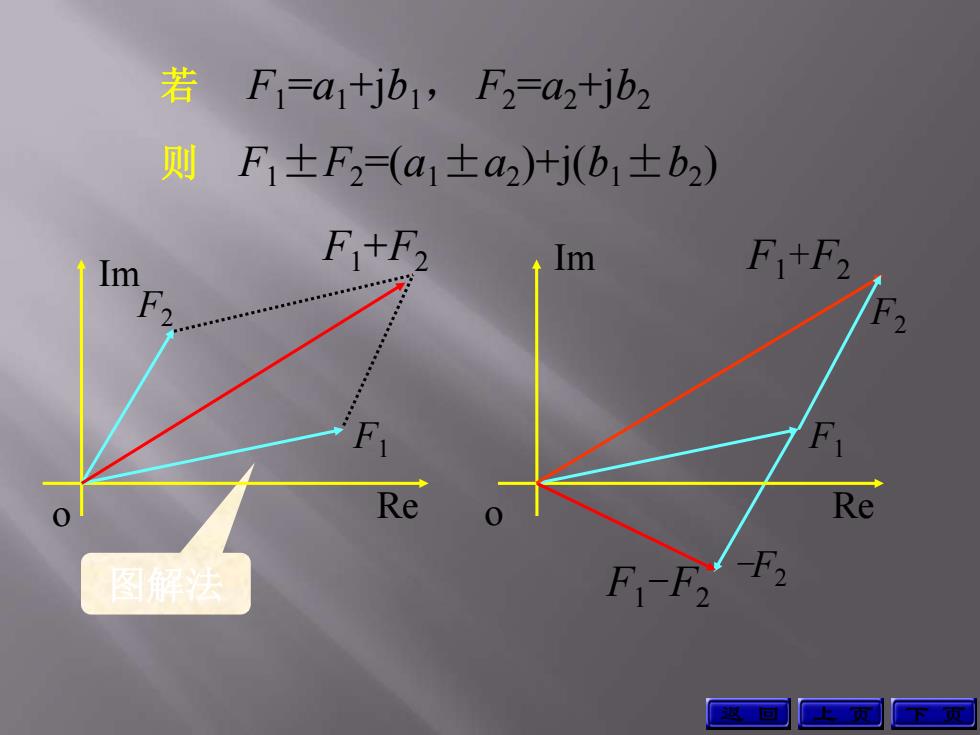
F=atjb,F2=a2+jb2 则F,±F2(a1士a2十j(b1±b2) F1+F2 m F+F2 Re Re 图解法 F-F2-F2

则 F1±F2=(a1±a2 )+j(b1±b2 ) 若 F1 =a1+jb1， F2 =a2+jb2 图解法 上 页 下 页 F1 F2 Re Im o F1+F2 -F2 F1 Re Im o F1-F2 F1+F2 F2 返 回