非线性物理:分形物理 (b) (c) (d)
非线性物理:分形物理

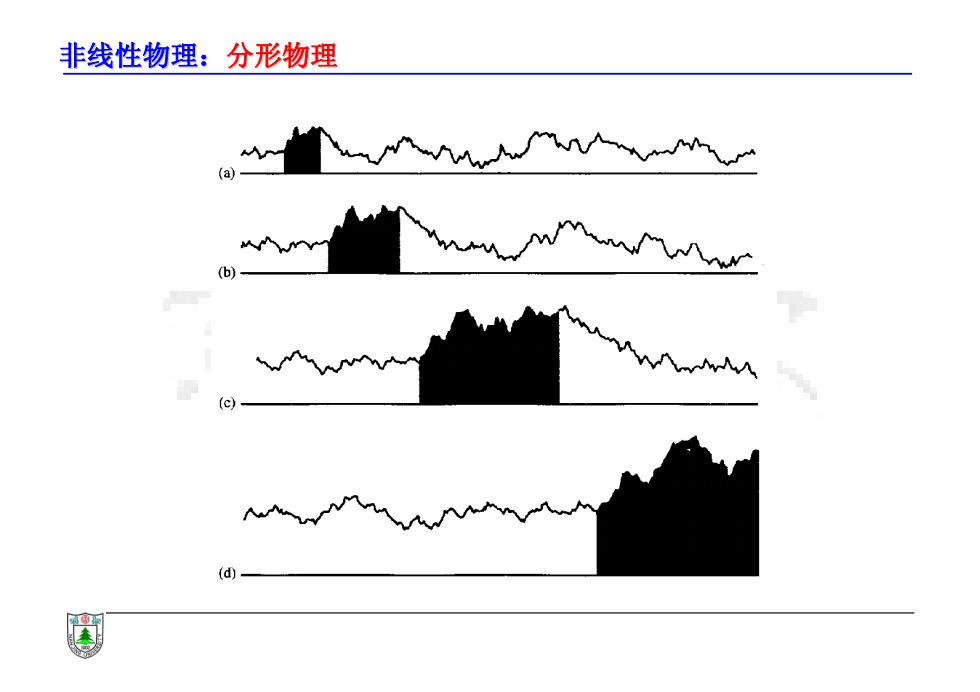
非线性物理:分形物理 以普通布朗运动为例说明其分维:因为x()和x(2)/2a自相似, 对t∈0,W区间,用尺度r去测量得到N个单元N=1/m)。 现在用尺度r2去测量t∈0,1/2区间内单元个数。因为指数标度的 缘故,t∈/0,1/2/区间内单元数变成t∈0,1/区间内单元数的1/2倍 ,再用r/2的尺度去测量,就会测得2N/2个单元。 对t∈1/2,1W区间也是一样,总共在t∈0,1区间测得22-N个单元。 依此类推,用尺度2测量,得到22yN个单元,维数D是: D=me-,-a B=2a+1=22-D)+1=5-2D
非线性物理:分形物理 • 以普通布朗运动为例说明其分维:因为 x(t) 和 x(2t)/2 自相似, 对 t[0,1]区间,用尺度 r 去测量得到 N 个单元(N=1/r)。 • 现在用尺度 r/2 去测量t[0,1/2]区间内单元个数。因为指数标度的 缘故, t[0,1/2]区间内单元数变成t[0,1]区间内单元数的1/2倍 , 再用 r/2 的尺度去测量,就会测得 2N/2个单元。 • 对t[1/2,1]区间也是一样,总共在t[0,1]区间测得22-N个单元。 • 依此类推,用尺度 r/2k 测量,得到(22-)kN个单元,维数D是:

非线性物理:分形物理 标度对称性:物理学实例 ·临界现象中的标度不变性: a(T-T) 5[(T-T1=入(T-T) 湍流体系中,相距为r的两点速度差)是随机信号, Kolmogorov证明: Av(r)a ra,a=- 3 B=2C+1 ((Av(r))cr3,s(k)k
非线性物理:分形物理 标度对称性:物理学实例 • 临界现象中的标度不变性: • 湍流体系中,相距为 r 的两点速度差 v(r) 是随机信号, Kolmogorov证明: