安徽理工大学：《智能控制及仿真》课程教学资源（课件讲义）第11章 迭代学习控制

在学习开始时，系统的初始状态为x(O)。学习控制的任 务为通过学习控制律设计"()，使第i+1次运动误差()减 少。 采用三种基于反馈的迭代学习控制律： (1)闭环D型： u()）=u()+K(a()-qk() (11.10) (2)闭环PD型： u41()=u()+K,(q()-qk41()+K(g:()-q1() (11.11) (3)指数变增益D型： u1()=ue()+K,(qa()-qk()+K(aa()-4H() 11.12)

在学习开始时，系统的初始状态为 。学习控制的任 务为通过学习控制律设计 ，使第 次运动误差 减 少。 采用三种基于反馈的迭代学习控制律： （1）闭环D型： （11.10） （2）闭环PD型： （11.11） （3）指数变增益D型： （11.12） x0 0 ui1 t i 1 ei1 t uk1 t  uk t  Kd q d t q k1 t uk1 t  uk t  Kp qd t qk1 t  Kd q d t q k1 t uk1 t  uk t  Kp qd t qk1 t  Kd q d t q k1 t

11.4.2仿真实例 针对二关节机械手，介绍一种机器人PD型反馈迭代学习控 制的仿真设计方法。针对二关节机器人控制系统式(11.9)， 各项表示为： D=[4,]a d=dl+d2(+2+212cosg2)+1,+12 d2=d21=d,(6+l12cos92) d2=d6+12+l3 C=[ca cu=hg2:cr2=hg+hgz,ca=-hgy C22=0,h=-m2hle2 singz G-[G,G] G=(dile+dh)gcosg+d2l2gcos(gi+92),G2=d2l2gcos(g+92)

11.4.2 仿真实例 针对二关节机械手，介绍一种机器人PD型反馈迭代学习控 制的仿真设计方法。针对二关节机器人控制系统式（11.9）， 各项表示为：           2 2 2 2 2 11 1 1 2 1 2 1 2 2 1 2 2 12 21 2 2 1 2 2 2 22 2 2 2 2 2 2 11 2 12 1 2 21 1 22 2 1 2 2 T 1 2 1 1 1 2 1 1 2 2 1 2 2 cos cos 0 sin g cos g cos ij c c c c c c ij c c c d d d l d l l l l q I I d d d l l l q d d l I l c c hq c hq hq c hq c h m l l q G G G d l d l q d l q q                                      D C G  ，   ， ， ， ，G2  d2 l c2g cosq1  q2 

干扰项为t=[03sint0.(1-e)门机器人系统参数 为d=d2=1kg,1=h=0.5m,a=lo2=0.25m,1=2=0.1kgm2,g=9.81m/s2。 采用三种闭环迭代学习控制律，其中M=1为D型迭代学 习控制，M=2为PD型迭代学习控制，M=3为变增益指数D型迭 代学习控制。 两个关节的位置指令分别为sin(3)和cos(3)，为了保 证被控对象初始输出与指令初值一致，取被控对象的初始状 态为x(O)=[031'。取PD型迭代学习控制，即M=3,仿 真结果如图11-1至图11-3所示

干扰项为 机器人系统参数 为 ， ， ， ， 。 采用三种闭环迭代学习控制律，其中 为D型迭代学 习控制， 为PD型迭代学习控制， 为变增益指数D型迭 代学习控制。 两个关节的位置指令分别为 和 ，为了保 证被控对象初始输出与指令初值一致，取被控对象的初始状 态为 。取PD型迭代学习控制，即 ，仿 真结果如图11-1至图11-3所示。   T d 0.3sin 0.1 1 e t  t        1 2 d  d 1 kg 1 2 l  l  0.5m 1 2 l c  l c  0.25m 2 1 2 I  I  0.1 kg m 2 g  9.81 m/s M 1 M2 M3 sin(3t) cos(3t)     T x 0  0 3 1 0 M  3

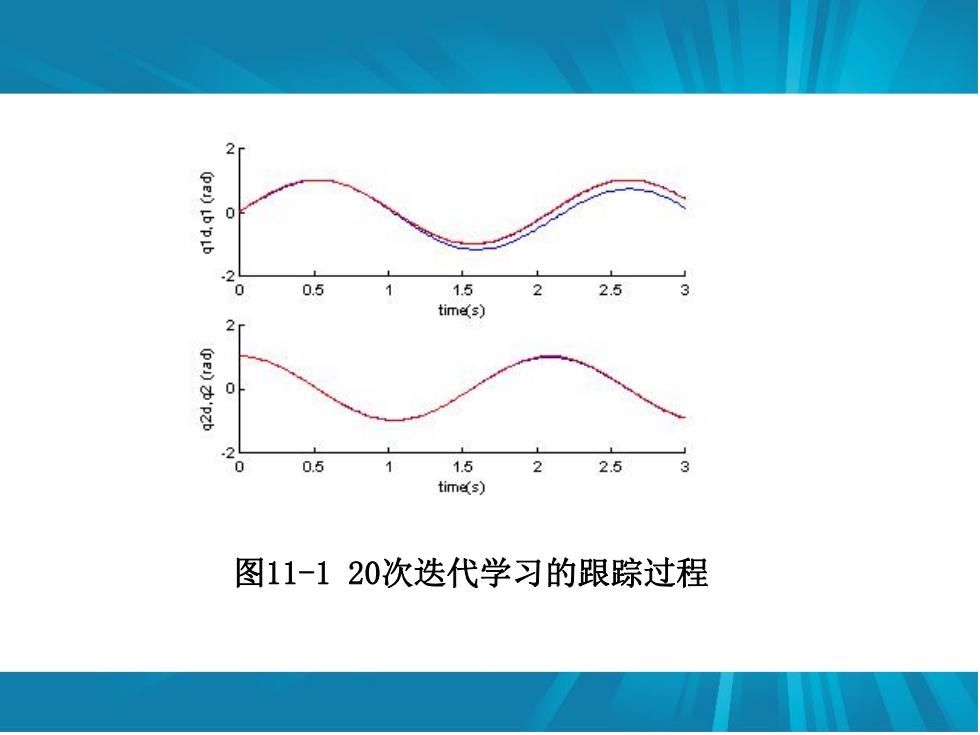
0 0 0.5 1.5 2.5 tim以s) 0 0.5 1.5 2 2.5 tim区s) 图11-120次迭代学习的跟踪过程

图11-1 20次迭代学习的跟踪过程

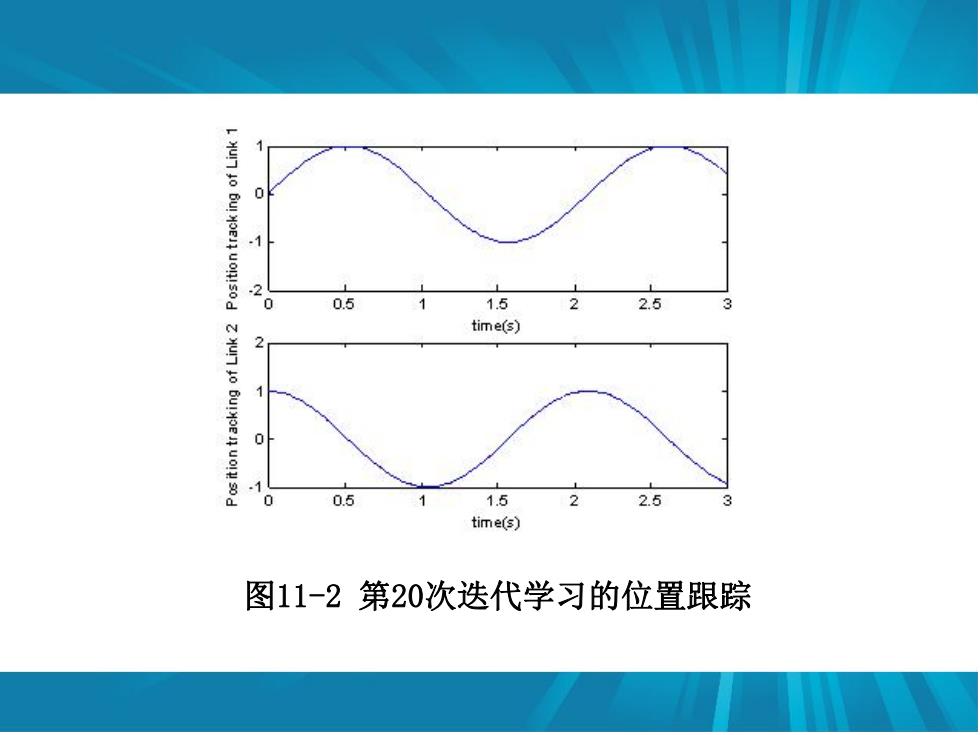
1 2 0.5 7 1.5 2 2.5 time(s) 0.5 1.5 2 2.5 time(s) 图11-2第20次迭代学习的位置跟踪

图11-2 第20次迭代学习的位置跟踪