安徽理工大学：《智能控制及仿真》课程教学资源（课件讲义）第11章 迭代学习控制

Change of maximum absolute value of error1 and error2 with times i 0.3 0.3* 0.25 0.2 0.15 0.1 0.05 5 10 15 times 图11-320次迭代过程中误差范数的收敛过程

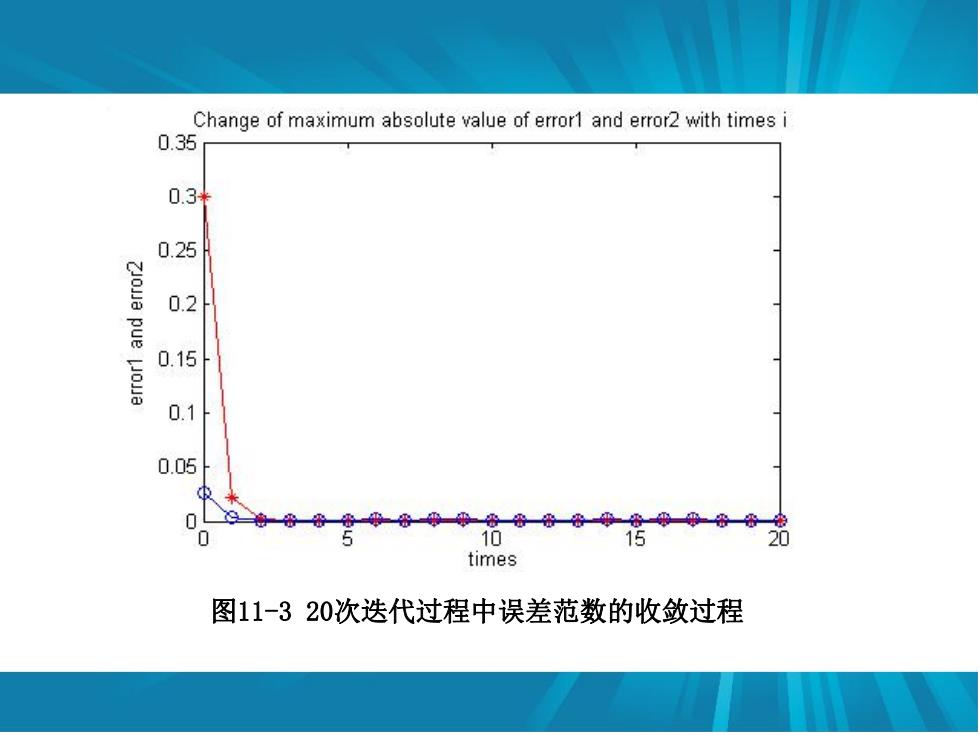
图11-3 20次迭代过程中误差范数的收敛过程

11.5线性时变连续系统迭代学习控制 11.5.1系统描述 Arimoto等[24]给出了线性时变连续系统 ()=A()x()+B()u() (11.13) y(t)=C()x() 的开环PD型迭代学习控制律 间=u,0+r+l+町e. (11.14) 其中下，L,平为学习增益矩阵

11.5 线性时变连续系统迭代学习控制 11.5.1 系统描述 Arimoto等[24]给出了线性时变连续系统 （11.13） 的开环PID型迭代学习控制律 （11.14） 其中 ， ， 为学习增益矩阵。                 t t t t t t t t    x A x B u y C x  1       d d d k k k t t t t t             u u Γ L Ψ e Γ L Ψ

11.5.2控制器设计及收敛性分析 定理1若由式（11.13)和式（11.14)式描述的系统满足 如下条件241： (1)II-C()B()r(训≤p<1 (2)每次迭代初始条件一致，即x(0)=x(k=1,2,3,…)y(0)=y(0) 则当k→o时，有()→y(),1e[0,T]。 证明： 由式(11.13)及条件式(2)得(0)=C(O)=C(0)=y(0) 则c(o)=0(k=0,12,),即系统满足初始条件

11.5.2 控制器设计及收敛性分析 定理1 若由式（11.13）和式（11.14）式描述的系统满足 如下条件[24]： （1） （2）每次迭代初始条件一致，即 则当 时，有 ， 。 证明： 由式（11.13）及条件式（2）得 则 ，即系统满足初始条件。 I  CtBtΓt   1 xk 0  x0 k 1,2,3,,y0 0  yd 0 k   yk t  yd t t 0,T  yk1 0  Cxk1 0  Cxk 0  yk 0 ek 0  0k  0,1,2,

非齐次一阶线性微分方程)=A()x(④+B()u()的解为： x()=Cep[Adr)Adr()u()exp(-Adr =Cexp(Ar)+exp(A)[B()u()exp(-Az)lr=Cexp(A)+[exp(A(-z))B()u()r 取(t,)=exp(A-r》,则 x()-x()=,)B(r(u()-u(r 由于e)=y)-y0,e)=y)-y0,则 ek(O)-e(O)=yx()-yH()=Ct)&,()-x() =∫C)tt)B((u()-(ar 即 e()=e.()-SC()O(t.z)B(z)(uu(z)-u()Hir

非齐次一阶线性微分方程 的解为： 取 ，则 由于 ， ，则 即 x t  At xt Btut                                0 0 0 0 0 0 exp d exp d exp d d exp exp exp d exp exp d t t t t t t t t t t                               x C A A B u A C A A B u A C A A B u Φt,   exp At     1         1   0 , d t k k k k t t t       x x Φ  B  u  u   ek t yd tyk t ek1 t yd tyk1 t                         1 1 1 1 0 , d e e y y C x x C Φ B u u k k k k k k t k k t t t t t t t t t                  1           1     0 e e C Φ , B u u d t k k k k t t t t           